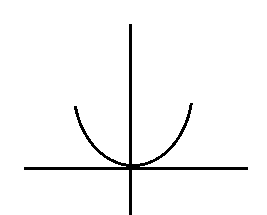本文主要是介绍CNN入门讲解:什么是激活函数(Activation Function),希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
各位看官老爷们
( ̄▽ ̄)/
这里是波波给大家带来的CNN卷积神经网络入门讲解
不定期我将给大家带来绝对原创,脑洞大开,幽默风趣的深度学习知识点入门讲解
希望大家多多支持,多多关注
微信公众号:follow_bobo
知乎号:蒋竺波
啦啦啦(~ ̄▽ ̄)~
新年好
好久不见啊
想我吗
我们前面说了卷积层,再到下采样层
根据网络结构
我们应该又进入到卷积层
不
我不去
学业繁忙
告辞!
最近实在很忙啊
在做一个AI 医疗项目,主要检测心脏疾病
哎,一直没啥进展
老板是个美国人,很Push, 经常询问进度
他原来已经创立了一家公司,卖了几千万美元
现在重新开始创业
说实话,人家创业的精神实在值得我们学习,身价几千万了,还和我们一起在一线奋斗。很多事都亲力亲为。每当我们有问题解决不出,他就会想办法去解决,每次给他发邮件,他都会立马回复,并且内容及其详细,好几次他的当地时间凌晨3,4点还能立马给我回复(他人在美国)。每次meeting,他都会积极调动我们思维每次说话,好几次我一点progress都没有,他都会努力找了点progress来表扬我,老感动了。
扯远了,我们来看激活函数
实际上,从下采样层出来的结果,不是又到卷积层,而是进入了一个激活函数(activation function)
在讨论激活函数之前
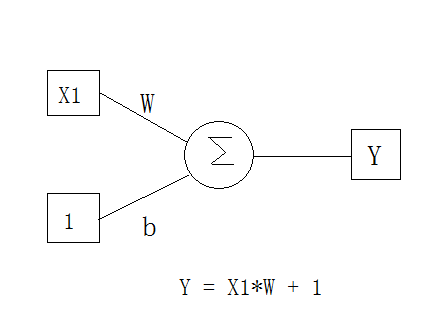
我们先来看一个普通的神经网络
有多普通
这应该就是一个小学的线性数学公式吧
没错,其实你小学就已经学了神经网络了
这个神经网络,可以轻松解决普通的线性二分类问题
如下
So easy
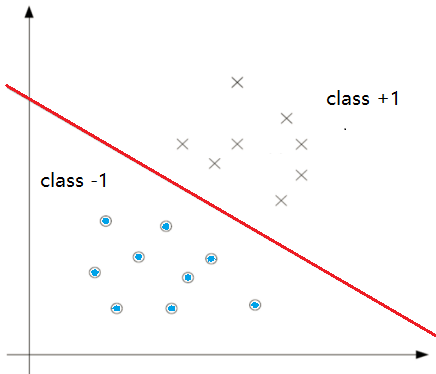
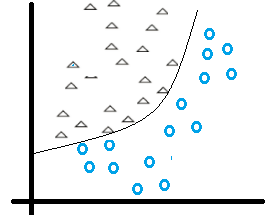
可是现实生活中
更多的是这种复杂的二分类
你会发现,一个普通的线性神经网络无论怎么移动和反转
都无法将上图分类
因为给出的样本点就不是线性可分的
我记得高数曾教过我们泰勒公式
意思就是一个函数f(x) 可以由N次多项式来表达或者近似
Ok,那我们假设
通过不断叠加简单神经网络得到一个复杂神经网络
最后这个复杂的神经网络可以将上述圆圈和三角形分类
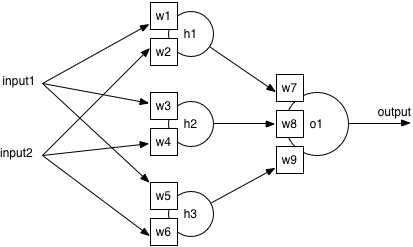
那我们画一个复杂的
Output = w7(input1*w1 +input2*w2)+w8(input1*w3+input2*w4)+w9(input1*w5+input2*w6)
太复杂,看不懂没关系
我们调整一下:
Output = input1(w1*w7+w3*w8+w9*w5)+input2*(w2*w7+w4*w8+w6*w9)
我们假设Output = 0
那么input1 = input2*( w2*w7+w4*w8+w6*w9)/(-w2*w7+w4*w8+w6*w9)
最后又回到了y= X*W的线性模式
也就是说,现在的神经网络学习能力非常有限
无法去解决非线性问题
叠加简单神经网络解决不了非线性分类问题
其实大数早已经教过我们
线性函数具有可加性和齐次性
任意线性函数连接都可以等价为一个单一线性函数
好了
第一个问题(゚▽゚*)
线性神经网络没法解决非线性问题
那我们就换种思路
我们能不能把线性神经网络,转成非线性的
也就是把分隔直线转换成曲线
是不是就能解决非线性分类
怎么转
我们从最简单的神经网络 Y = W * X +B入手
然后变成最简单的非线性神经网络Y = W*X*X+B
这是一个普通Y = X*X 的表达式
Y = W*X*X+B 经过一系列运算(理想的)
我们得到了如下:
变成曲线后,好像可以把这两类区分开诶
是不是有点理解了
哦哦
原来如此
第二个问题(゚▽゚*)
我们的神经网络(还是最简单的)
Y =W*X +B
根据input X的值,我们会得到Y值
所以我们需要一个函数可以对得到的Y值进行分类的
比如Y大于0 ,分类为1
小于0 ,分类为0
第三个问题(゚▽゚*)
对于神经网络
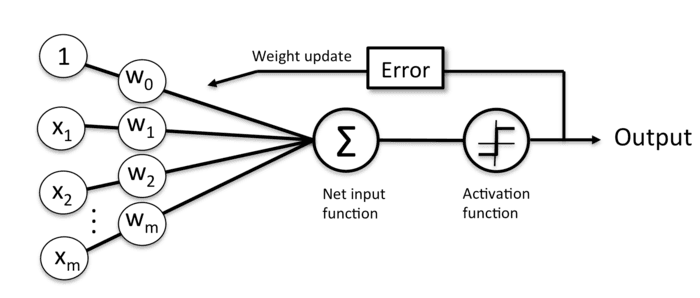
Y = W*X +B
我们知道,我们需要算出输出误差error (output Y - target Y) 来更新权值
假设我们的输入X的绝对值特别大,或者无限大,那么Y值就会特别大
直接导致error太大
更新出来的权值没有意义,或者无法更新权值
第四个问题(゚▽゚*)
这个问题涉及到反向传播(back propagation),可能很多小伙伴会看不懂
你以为我会仔细讲吗?
不
我不会
初学者建议你跳过下面一段
哈哈哈哈哈︿( ̄︶ ̄)︿
如果我们的神经网络函数是线性的
那么它的导数就是个常数
意味着什么
意味着gradient和X 无关了,也就是很输入无关了
我们在做反向传播的时候
Gradient 的改变也变成常数
和输入的改变X(delta(x)) 无关了
综合以上四个问题ヽ( ̄▽ ̄)ノ
这个时候,就是我们激活函数(Activation Function)上场了
因为我们最终要解决一个分类问题(classification)
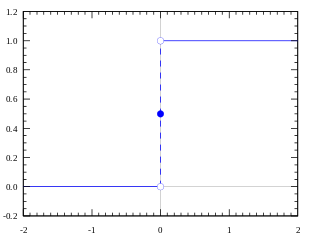
那我们还是从最简单的二分类非线性激活函数开始---阶跃函数(Step Function)
当输入(也就是神经网络Y的输出)大于0就被分类到1(100% 被激活 ),小于0就分到0,(没有被激活)
可是激活值只有100%或者0%未免太不负责了
我们希望它可以是0%---100%任意值
值越大,激活程度越高 对于分类,也就意味着它属于这一类的概率越大
综上所述
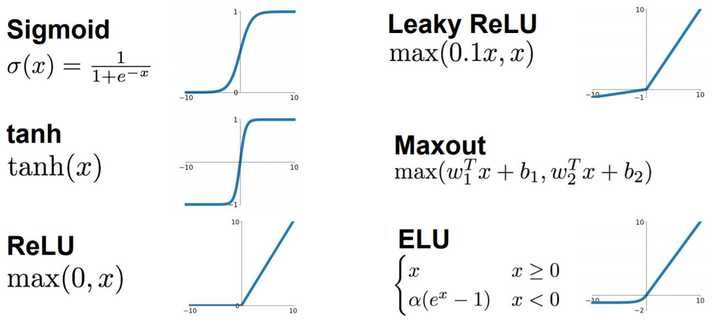
各种激活函数层数不穷,各有优缺点
比如大家都经常听到或者用到的
Relu, sigmoid,tanh等等
你看sigmoid 只会输出正数,以及靠近0的输出变化率最大,tanh和sigmoid不同的是,tanh输出可以是负数,ReLu是输入只能大于0,如果你输入含有负数,ReLu就不适合,如果你的输入是图片格式,ReLu就挺常用的。
因为每个激活函数都要考虑输入输出以及数据变化
所以要谨慎选择
太细的这里就不讲了ヽ( ̄▽ ̄)ノ
因为它们涉及到比较深的一些理论,不符合我们入门的这个主题
下次我再单独讨论讨论他们
好吧,其实是太忙,没时间写了(~ ̄▽ ̄)~
后面的话,等我把基础讲完了
我再把这些比较深的东西串一串
结合结合代码什么
毕竟你懂的再多
不会写代码,有何用︿( ̄︶ ̄)︿
这篇关于CNN入门讲解:什么是激活函数(Activation Function)的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!