操作系统课设-银行家算法VS2022

目录

1 目的和要求

2 银行家算法的数据结构

3 进程请求时的资源处理

4 安全性算法的设计思路

5 调试与分析

6 C语言源代码

7 心得体会

1 目的和要求

银行家算法是避免死锁的一种重要方法，能够有效的在资源分配的过程中，对系统的安全性进行检测。通过银行家算法设计与实现，可以加深对死锁的理解，掌握死锁的预防、避免、检测和解除的基本原理，重点掌握死锁的避免方法━银行家算法。初步具有研究、设计、编制和调试操作系统模块的能力。

能够考虑社会、健康、安全、法律、文化及环境等因素的影响，针对银行家算法避免死锁进行建模，设计实验方案，运用恰当的集成开发工具编程模拟实现上述算法。

对程序要求:

1. 有录入界面，动态录入进程个数、资源种类数、诸进程对各类资源的最大需求、TO时刻系统为诸进程已分配的资源数以及系统中各类资源的资源总数;
2. 能够判断TO时刻系统是否安全，进程之间能否无死锁的运行下去，若能输出安全序列;
3. 有输出界面，能够从录入界面模拟进程又提出新的申请，根据银行家算法判断请求是否能得到满足，并输出当前时刻下诸进程对各类资源的需求列表及系统可用资源数，若能输出安全序列，若不能分配输出无法分配的原因;

对报告要求：

1. 报告要体现算法设计和分析的能力，要体现建模及算法设计与实现的过程，形成设计文档;
2. 要对各种资源请求情况的运行结果截图并分析实验数据，分析产生不同结果的原因，得出有效结论;
3. 对本次设计进行总结，遇到什么问题、是如何解决的?总结实验仿真的局限性，指出实验设计方案的完善方向;
4. 报告要体现科技强国的核心价值观，科技报国的家国情怀和使命担当。具有探索未知、追求真理、勇攀科学高峰的科学精神以及以改革创新为核心的时代精神。

2 银行家算法的数据结构

可用资源向量Available [m]

m为系统中资源种类数，Available[j]=k表示系统中第j类资源数为k个。

最大需求矩阵Max[n][m]

n为系统中进程数，Max[i][j=表示进程i对j类资源的最大需求数为k。

分配矩阵Allocation[n][m]

Allocation[i][j]=k表示进程i已分得j类资源的数目为k个。

需求矩阵Need[n][m]

Need[i][j]=k 表示进程i还需要j类资源k个。

Need[i][j]=Max[i][j]-Allocation[i][j]

3 进程请求时的资源处理

假设在进程并发执行时进程i提出请求j类资源k个后，表示为Request,[j]=k,系统按下述步骤进行安全检查:

如果Request,≤Need;则继续以下检查，否则显示需求申请超出最大需求值的错误。

〉如果Request,≤Available则继续以下检查，否则显示系统无足够资源，P;阻塞

等待。

系统试探把要求的资源分配给进程i并修改有关数据结构的值:

Available = Available-Request, ;

Allocation;=Allocation; +Request; ;Need;=Need,-Request;;

系统执行安全性算法，检查此次资源分配后，系统是否处于安全状态，若安全，才正式将资源分配给进程i，以完成本次分配;否则将试探分配作废，恢复原来的资源分配状态，让进程P;等待。

4 安全性算法的设计思路

安全性算法

A.设置完成标志向量Finish[n]。

初始化:Finish[i] = false表示i进程尚末完成

B.从进程集合n设置Work[m]表示系统可提供给进程的各类资源数目。初始化:

Work = Available,

中找到一个能满足下述二个条件:Finish[i] = false , Need;≤Work如找到则执行步骤C，找不到则执行步骤D

C.当进程i获得资源后可顺利执行直到完成，并释放出分配给它的资源，表示如下:

work = work+Allocation; ; Finish[i]=true ;转执行步骤B。

D.如果所有的Finish[i]=ture，则表示系统处于安全状态，否则系统处于不安全状态。

5 调试与分析

1.资源的初始分配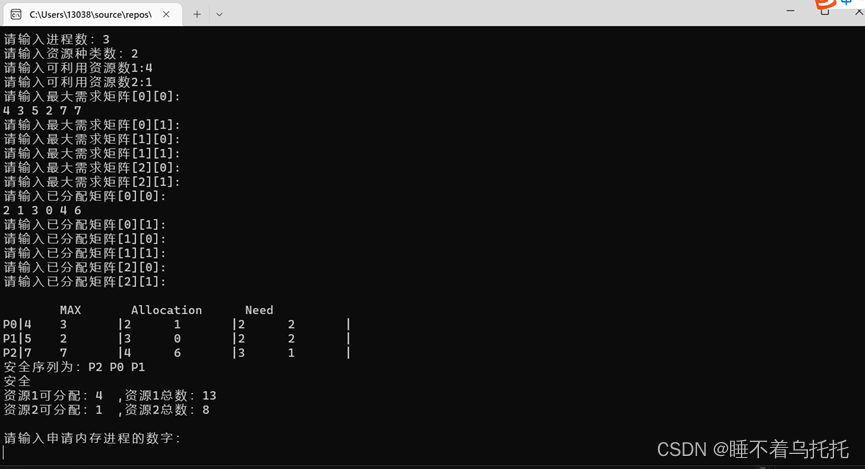（图1）

图1

2.尝试给P0分配资源2,2，提示请求资源数大于可利用资源数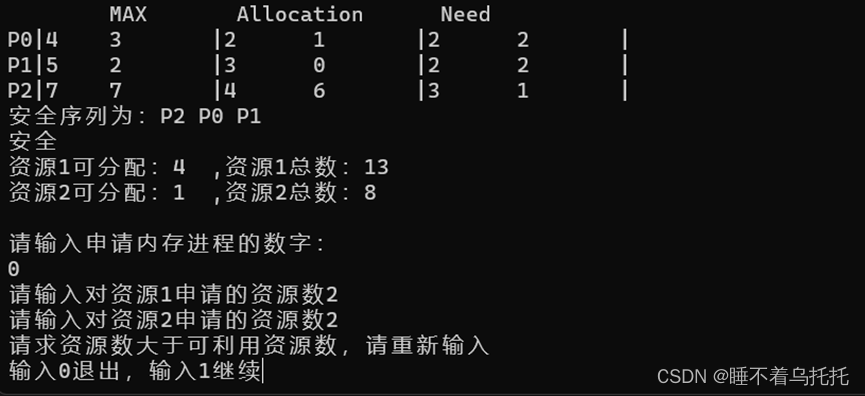（图2）

图2

3.尝试给P0分配资源3,2提示请求资源数大于所需资源数（图3）

图3

4.尝试给P0分配资源0,0，提示不安全撤销了分配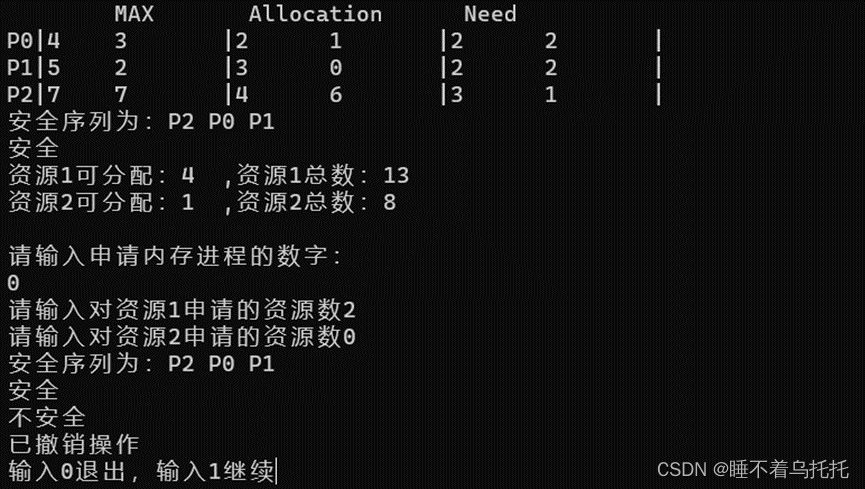（图4）

图4

5.尝试给P2分配资源1,1，提示安全，可利用资源和对应进程的资源需求随即发生更新（图5.1）（图5.2）

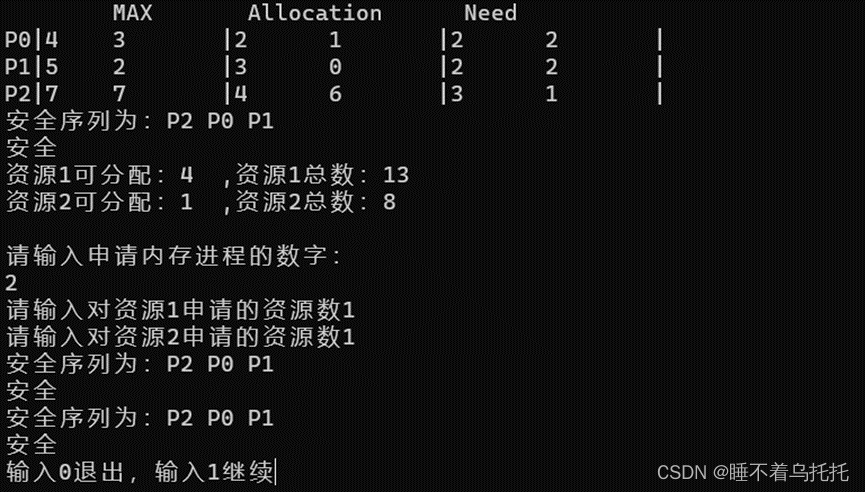图5.1

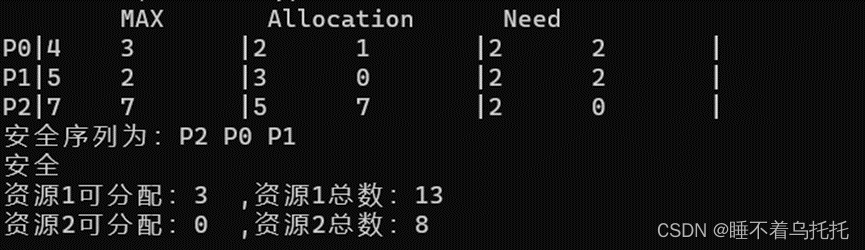图5.2

6.继续给P2分配资源2,0，进程达到需求结束后释放资源（图6.1）（图6.2）

图6.1

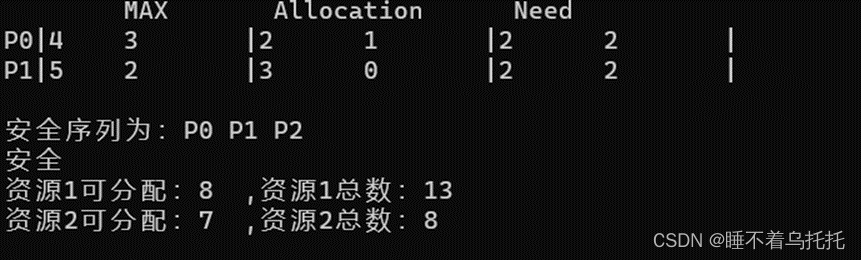图6.2

7.给P1分配资源2,2，进程达到需求结束后释放资源（图7.1）（图7.2）

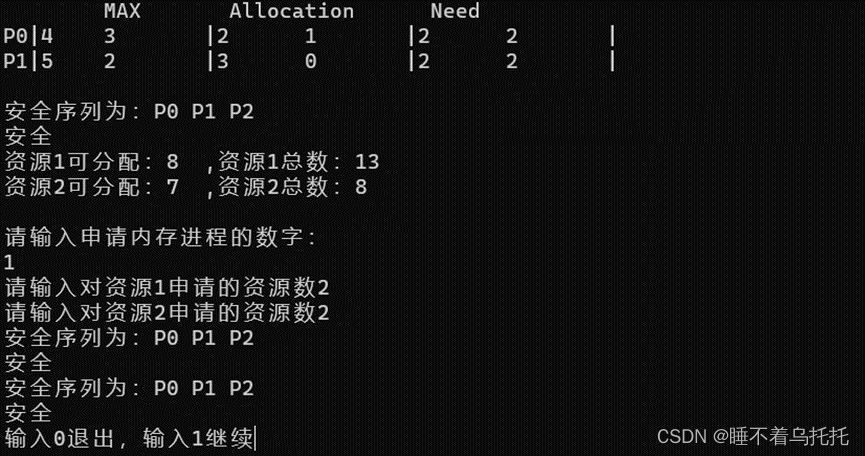图7.1

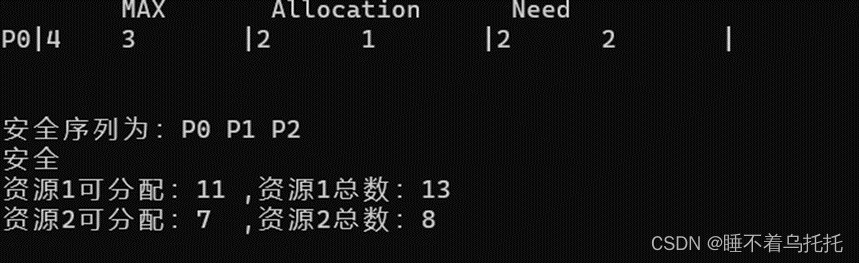图7.2

8.给P0分配资源2,2，进程达到需求结束后释放资源（图8.1）（图8.2）

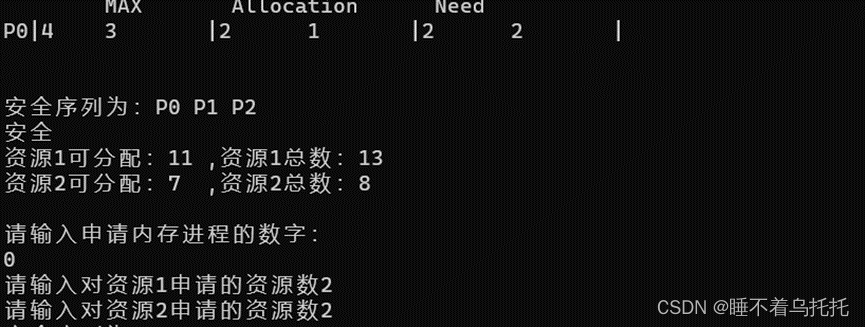图8.1

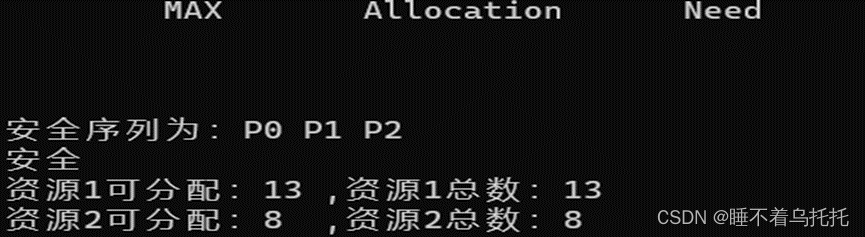图8.2

6 C语言源代码

安全性算法

int safety(int m, int n)//m进程数,n资源种类数
{int i, j, k, l, flag;int safe[MAX] = { 0 };//安全序列int count = 0; //安全序列个数for (i = 0; i < m; i++) {finish[i] = 0; //初始化完成标志 work[i] = available[i]; //可利用资源量初始化 }while (1){flag = 0; //完成标志for (j = 0; j < m; j++) {if (finish[j] == 0) //未完成进程{for (k = 0; k < n; k++){if (need[j][k] > work[k]) //判断资源是否满足 break;}if (k == n) //资源满足{for (l = 0; l < n; l++)work[l] += allocation[j][l];//更新可利用资源量safe[count] = j; //加入安全序列count++;finish[j] = 1; //更新完成标志 flag = 1;//更新完成标志}}} if (flag == 0) //无进程可运行 break;} if (count == m) //进程完成 {printf("安全序列为：");for (i = 0; i < m; i++)printf("P%d ", safe[i]);printf("\n安全\n");return 1;}else //不安全{printf("不安全\n");return 0;}
}

请求资源 

int requestResource(int p, int m, int n)//m进程数,n资源种类数
{int i, j, k; //判断请求资源是否满足 for (i = 0; i < n; i++){if (request[i] > need[p][i]){printf("请求资源数大于所需资源数，请重新输入\n");return 0;}} //判断请求资源是否满足for (j = 0; j < n; j++){if (request[j] > available[j]){printf("请求资源数大于可利用资源数，请重新输入\n");return 0;}} //满足请求 if (safety(m, n) == 1){for (k = 0; k < n; k++){available[k] -= request[k]; //更新可利用资源量allocation[p][k] += request[k]; //更新分配矩阵need[p][k] -= request[k]; //更新需求矩阵 }}}if (safety(m, n) != 1) //安全性算法撤销操作{for (k = 0; k < n; k++){available[k] += request[k]; //更新可利用资源量 allocation[p][k] -= request[k]; //更新分配矩阵need[p][k] += request[k]; //更新需求矩阵 }}printf("已撤销操作\n");}}

7 心得体会

这次课设是以银行家算法来进行，通过互联网上的相关渠道，了解了银行家算法是避免死锁作为一种事先预防死锁的策略，原理是在为各个进程分配资源的过程中不允许系统进去不安全状态，以此来避免死锁的发生。所谓安全状态，是指系统能按某种进程推进顺序为每个进程分配其所需资源，直至满足每个进程对资源的最大需求，使每个进程都可以顺利地完成。此时称该进程推进序列为安全序列，如果无法找到这样一个安全序列，则称系统处于不安全状态。

为了实现银行家算法，在系统中必须设置这样四个数据结构，分别用来描述系统中可利用的资源，所有进程对资源的最大需求，系统中的资源分配以及所有进程还需要多少资源的情况。当一个进程发出请求资源的请求后，如果它所请求的资源大于目前系统可利用资源则不予分配。如果小于可利用资源，则系统试探着把资源分配给该进程，并修改分配之后的资源数值。接着系统执行安全算法，检查此次资源分配后系统是否处于安全状态。若安全，才正式将资源分配给该进程，以完成本次分配。否则，将本次的试探分配作废，恢复原来的资源分配状态，让该进程等待。过程中遇到了许多问题，例如回收资源的代码如何实现，通过和同学们的讨论与互联网上相关内容的查询最终解决了问题。这次课设让我对操作系统的避免死锁这一概念的理解更加深入，学到了很多。