《Java小子怒闯数据结构九重天》第六重天——树

本专栏文章主要用于帮助Java使用者快速上手数据结构，刷算法题！

前言

自古以来数据结构界就分为九重天，据说冲破这九重天之后就可以去进攻算法界最终修炼最后成佬，受万人敬仰。

但是这谈何容易，因为每一重天都有神兽把守，想要冲破每一重天都必须收服守护的神兽才行。

守护九重天的神兽分别是：数组、字符串、栈、队列、链表、树、散列表、堆、图。可见他们的战斗力也是逐层增强的。想只凭靠自身的能力拿下他们谈何容易。

不过大家不必惊慌，我这里有一本上古秘籍《Java小子怒闯数据结构九重天》，里面有每一重天神兽的攻略。只要修炼者仔细钻研里面的每一篇，对九重天了如指掌之后，冲破这九重天也是易如反掌的。

今天为大家带来第六重天的攻略！

1.🌀树的基础知识

树的特点

（1）每一个节点有零个或多个子节点；
（2）没有父节点的节点，称之为根节点；
（3）每一个非根节点有且仅有一个父节点；
（4）除了根节点外，每个子节点可以分为多个不相交的子树；

如下就一棵树：

树的基本术语

• 节点的度： 一个节点含有的子树的个数称为该节点的度，图中节点 1 的度为 2 ，节点 3 的度为 3。

• 树的度： 一棵树中，最大的节点的度称为树的度上面示例中的树的度为 3。

• 叶节点或终端节点： 度为零的节点（示例中有五个叶子节点）。

• 父亲节点或父节点： 若一个节点含有子节点，则这个节点称为其子节点的父节点（示例中 1 为 2 和 3 的父节点，3 为 6、7、8 的父节点）。

• 孩子节点或子节点： 一个节点含有的子树的根节点称为该节点的子节点（示例中 2 和 3 为 1 的子节点， 6、7、8 为 3 的子节点）。

• 节点的层次： 从根开始定义起，根为第1层，根的子节点为第2层，以此类推。

• 兄弟节点： 具有相同父节点的节点互称为兄弟节点（2 和 3 就是兄弟节点）。

• 子孙： 以某节点为根的子树中任一节点都称为该节点的子孙（由一个节点派生出来的所有节点，都是这个节点的子孙节点）。

• 树的高度或深度： 树中节点的最大层次（示例中，树的深度为 4 ）。

• 节点的祖先： 从根到某一节点所经的分支上的所有节点称为这一节点的祖先节点（例如，1 和 2 都是 4 的祖先节点）。

• 森林： 由m（m>=0）棵互不相交的树构成的集合称为森林。

树的种类

• 无序树： 树中任意节点的子节点之间没有顺序关系，这种树称为无序树，也称为自由树。

• 有序树： 树中任意节点的子节点之间有顺序关系，这种树称为有序树。

• 二叉树： 每个节点最多含有两个子树的树称为二叉树。

• 完全二叉树： 对于一棵二叉树，假设其深度为d(d>1)。除了第d层外，其它各层的节点数目均已达最大值（即子节点数目为2），且第d层所有节点从左向右连续地紧密排列，这样的二叉树被称为完全二叉树，其中满二叉树的定义是所有叶节点都在最底层的完全二叉树。

• 平衡二叉树（AVL树）： 当且仅当任何节点的两棵子树的高度差不大于1的二叉树。

• 排序二叉树（二叉查找树（Binary Search Tree），也称二叉搜索树、有序二叉树,是一种特殊的二叉树，树中的节点，按照一定的顺序进行排列；

• 霍夫曼树（用于信息编码）： 带权路径最短的二叉树称为哈夫曼树或最优二叉树；

• B树： 一种对读写操作进行优化的自平衡的二叉查找树，能够保持数据有序，拥有多余两个子树；

看到这里千万不要被这么多树的种类吓到了，我们主要学习的其实只有二叉树，把二叉树学明白了其他的差不多也就能可以了，学明白二叉树做题基本没问题的。

所以接下来的内容我们均围绕着二叉树来进行学习！

2.🌀二叉树的基础知识

它有五种基本形态：二叉树可以是空集、根可以有空的左子树或右子树、或者左、右子树皆为空。如下：

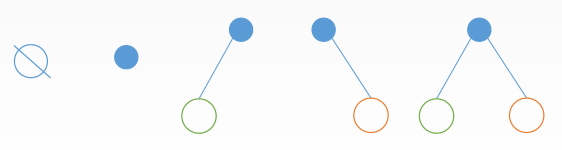
二叉树的性质

• 二叉树可以为空，而度为2的有序树至少有三个结点；
• 二叉树的孩子结点始终有左右之分，分别为左孩子与右孩子节点；
• 非空二叉树上的叶子结点数等于度为2的结点数加1，即n0=n2+1（度为0、1、2的节点个数为n0, n1, n2）；
• 非空二叉树上第k层上至多有2^k-1个结点（k≥1）；
• 高度为h的二叉树至多有2^h-1个结点（h≥1）；

特殊二叉树

满二叉树

一棵高度为h，且含有 2^h-1个结点的二叉树为满二叉树，如：

这里的 2^h -1是怎么来的呢？

因为高度为h的m叉树至多有（m^h-1）/（m-1）个结点

性质：

• 在二叉树中，对于编号为i的结点，若存在，其双亲的编号为 i/2 ，左孩子为2i，右孩子为2i+1

完全二叉树

设一个高度为h、有n个结点的二叉树，当且仅当其每个结点都与高度为h的满二叉树中编号1~n的结点一一对应时，称为完全二叉树。

这时候有人可能不明白了，满二叉树不是与完全二叉树一样吗？

并不是它们虽然长得很像，但是还是有一定区别的：完全二叉树的节点数是任意的，最后那一行可能不是完整的，其他位置均与满二叉树相同。

性质：

• 若i≤⌊n/2⌋，则结点i为分支结点，否则为叶子结点
• 叶子结点值可能在层次最后的两层上出现。对于最大层次的叶子结点，都依次排在最左边的位置上。
• 度为1的结点若存在，则可能有一个，且是编号最大的分支节点，并孩子结点一定是左结点。

二叉排序树

对任意结点若存在左子树或右子树，则其左子树上所有结点的关键字均小于该结点，右子树上所有结点的关键字均大于该结点，如：

平衡二叉树

树上任意结点的左子树和右子树的深度只差不超过1。
如下图，右边的二叉树因为根结点的左子树的左子树深度为2，右子树结点深度为0，所以不是平衡二叉树。

结点的深度是从根结点出发，向着叶子结点方向前进的

3.🌀实例化二叉树

根据二叉树的定义，它有两个节点，且有左右之分，称为左孩子和右孩子，则根据定义，可以定义出二叉树的节点类

class TreeNode<T>{public T val;public TreeNode left;//左孩子public TreeNode right;//右孩子public TreeNode(T val) {this.val = val;}
}

4.🌀二叉树的遍历

二叉树的常用操作就是遍历了，同样的无论二叉树的什么操作也都离不开遍历。

对于二叉树的遍历有：先序遍历、中序遍历、后序遍历、层次遍历。

先序遍历、中序遍历、后序遍历我们一般都是使用递归来实现。如果你不了解递归，不要紧，后面我们会进行讲解的。

先序遍历，若二叉树非空：

1. 访问根结点
2. 先序遍历左子树
3. 先序遍历右子树

代码如下：

// 先序遍历
void preOrder(TreeNode root) {if (root == null) {return;}System.out.print(root.val + " ");preOrder(root.left);preOrder(root.right);
}

中序遍历，若二叉树非空：

1. 中序遍历左子树
2. 访问根结点
3. 中序遍历右子树

代码实现：

// 中序遍历
void inOrder(TreeNode root) {if (root == null) {return;}inOrder(root.left);System.out.print(root.val + " ");inOrder(root.right);
}

后序遍历，若二叉树非空：

1. 后序遍历左子树
2. 后序遍历右子树
3. 访问根结点

代码实现：

// 后序遍历
void postOrder(TreeNode root) {if (root == null) {return;}postOrder(root.left);postOrder(root.right);System.out.print(root.val + " ");
}

而是用栈先进后出适合模拟深度优先遍历也就是递归的逻辑。

层次遍历我们一般是需要借用一个辅助数据结构（队列）来实现，队列先进先出，符合一层一层遍历的逻辑。

代码如下：

void check(TreeNode node) {if (node == null) return;Queue<TreeNode> que = new LinkedList<TreeNode>();que.offer(node);while (!que.isEmpty()) {int len = que.size();while (len > 0) {TreeNode tmpNode = que.poll();System.out.print(tmpNode.val + " ");if (tmpNode.left != null) que.offer(tmpNode.left);if (tmpNode.right != null) que.offer(tmpNode.right);len--;}}
}

5.🌀二叉树进阶练习

Leetcode 226. 翻转二叉树

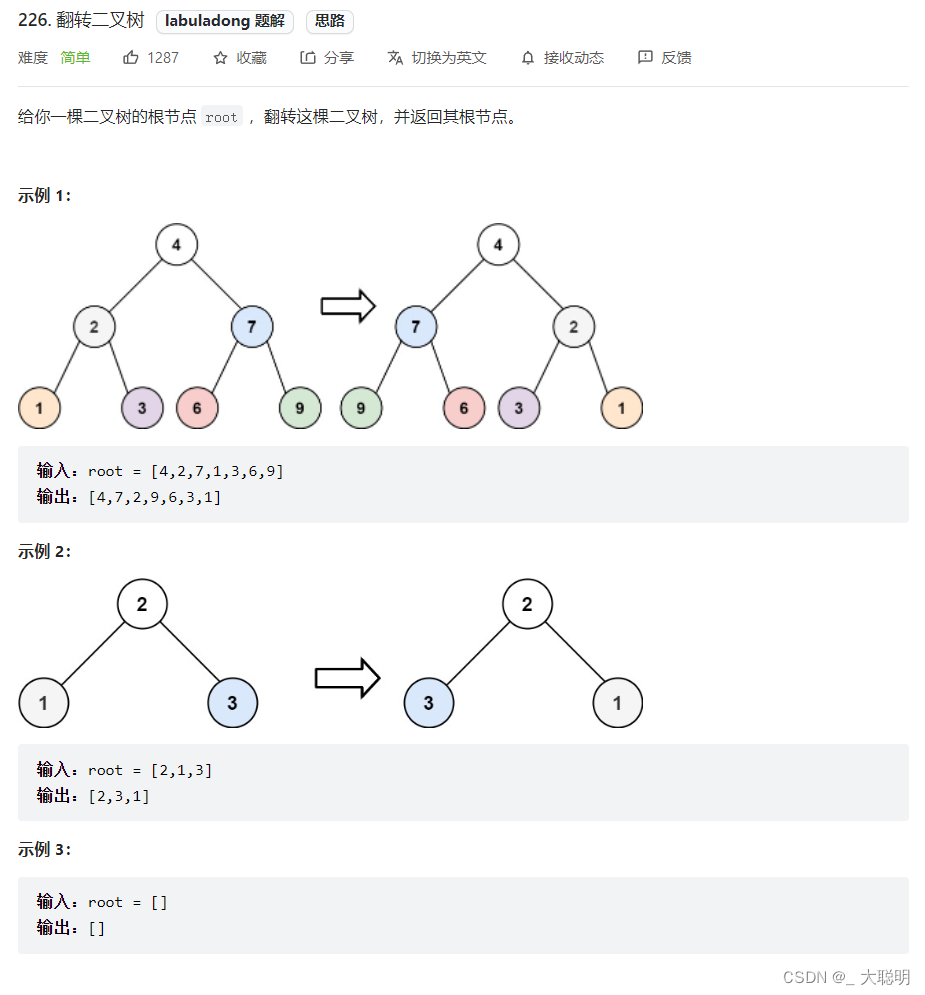
题解：

思路一

根据题目的输入和输出，输出的左右子树的位置跟输入正好是相反的，于是我们可以递归的交换左右子树来完成这道题。

代码如下：

/*** Definition for a binary tree node.* public class TreeNode {*     int val;*     TreeNode left;*     TreeNode right;*     TreeNode() {}*     TreeNode(int val) { this.val = val; }*     TreeNode(int val, TreeNode left, TreeNode right) {*         this.val = val;*         this.left = left;*         this.right = right;*     }* }*/
class Solution {public TreeNode invertTree(TreeNode root) {//递归函数的终止条件，节点为空时返回if(root==null) {return null;}//下面三句是将当前节点的左右子树交换TreeNode tmp = root.right;root.right = root.left;root.left = tmp;//递归交换当前节点的 左子树invertTree(root.left);//递归交换当前节点的 右子树invertTree(root.right);//函数返回时就表示当前这个节点，以及它的左右子树//都已经交换完了return root;}
}

思路二

我们还可以使用非递归的方法。使用层次遍历的方式继续调换每一个节点的左右子树。

class Solution {public TreeNode invertTree(TreeNode root) {if(root == null) {return root;}//使用辅助队列来实现层次遍历Queue<TreeNode> que = new LinkedList();que.offer(root);while(!que.isEmpty()) {int size = que.size();while(size > 0){TreeNode tempNode = que.poll();//下面三句是将当前节点的左右子树交换TreeNode temp = tempNode.right;tempNode.right = tempNode.left;tempNode.left = temp;if (tempNode.left != null) que.offer(tempNode.left);if (tempNode.right != null) que.offer(tempNode.right);size--;}}return root;}
}

结语

恭喜你修炼到这里，你已经基本有了收服神兽树的能力。神兽树是我们到进攻算法界最重要的能力之一。后面在算法界修炼的时候很多算法都是根据树来学习的，所以大家对于树不可懈怠。

感兴趣的修炼者可以关注下面公众号，会提前更新并且推送！

持续更新中…