带式输送机的主动速度控制（5）

 带式输送机完成主动速度控制，首先要确定带式输送机调节后的期望速度（前面已经介绍过），其次是选择合适的加速度、调节时间使得带式输送机的速度达到期望速度。这里介绍一种ECO（estimation-computation-optimization）方法，顾名思义就是先估计，再计算，最后优化。这种ECO方法经常被用来确定速度调节的时间，它是首先估计参数的值，然后根据一些已知理论计算调节时间值，最后根据仿真/实际情况再试图找到参数的最佳数值。

输送带的张力最大值往往出现在驱动滚筒的前端，带式输送机为避免输送带出现张紧风险所提供的最大驱动力 由下面公式(1)确定：

输送带与驱动滚筒之间不打滑的最大驱动力 由下面公式（2）确定：

电动机工作过热的最大驱动力 由下面公式（3）确定：

充分考虑这三者情况后，带式输送机的最大瞬态运行的驱动力应该是这三种驱动力的最小值：

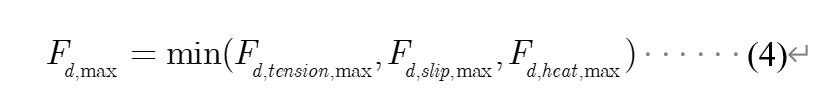
带式输送机的运动阻力由主阻力、二次阻力、倾斜阻力和特殊阻力组成，水平带式输送机的主阻力和二次阻力占总阻力的95%以上。因此，可以忽略水平带式输送机的倾斜阻力和特殊阻力，然后将主要阻力和二次阻力之和近似为：

根据牛顿第二运动定律，带式输送机自身所能达到最大加速为：

驱动电机无法进行回馈制动操作时，带式输送机在减速期间的最大加速度由下式可得：

估算-计算部分已经完成，接下来就需要搭建带式输送机的仿真模型，重复以上步骤进行验证计算的结果是否要求，若不满足要求，则进一步优化结果。