risk-jianmo整体流程梳理

本文主要是介绍risk-jianmo整体流程梳理，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

1. 加载数据与探索

1. 数据探索

from sklearn.metrics import roc_auc_score, roc_curve, auc  
from sklearn.model_selection import train_test_split  
from sklearn.linear_model import LogisticRegression   
import numpy as np
import xgboost as xgb  
import toad, math df = pd.read_csv("scorecard.txt")  
# 探索性数据分析
toad.detector.detect(df) 

2. 样本切分

ex_lis = ['uid', 'samp_type', 'label']  # 指定不参与训练列名  
ft_lis = list(df.columns)  # 参与训练列名  
for i in ex_lis:      ft_lis.remove(i) 
# 开发样本、验证样本与时间外样本(验证样本)  
dev = df[(df['samp_type']=='dev')]
val = df[(df['samp_type']=='val')]  
off = df[(df['samp_type']=='off')] 

2. 特征筛选

      可以使用缺失率、IV、相关系数进行特征筛选。但是考虑到后续建模过程要对变量进行分箱处理，该操作会使变量的IV变小，变量间的相关性变大，因此此处可以对IV和相关系数的阈值限制适当放松，或不做限制。

dev_slct1, drop_lst= toad.selection.select(dev, dev['label'], empty=0.7, iv=0.03, corr=0.7, return_drop=True, exclude=ex_lis) 
print("keep:", dev_slct1.shape[1],  "drop empty:", len(drop_lst['empty']), "drop iv:", len(drop_lst['iv']),  "drop corr:", len(drop_lst['corr']))
# keep: 12; drop empty: 0; drop iv: 1; drop corr: 0

3. 卡方分箱

combiner = toad.transform.Combiner()  # 得到切分节点  
combiner.fit(dev_slct1, dev_slct1['label'], method='chi', min_samples=0.05, exclude=ex_lis)   
bins = combiner.export()  # 导出分箱的节点 
print(bins)
{'td_score': [0.7989831262724624],'jxl_score': [0.4197048501965005],'mj_score': [0.3615303943747963],'zzc_score': [0.4469861520889339],'zcx_score': [0.7007847486465795],'person_info': [-0.2610139784946237, -0.1286774193548387, -0.05371756272401434, 0.013863440860215051, 0.06266021505376344, 0.07885304659498207],'finance_info': [0.047619047619047616],'credit_info': [0.02, 0.04, 0.11],'act_info': [0.1153846153846154, 0.14102564102564102, 0.16666666666666666, 0.20512820512820512, 0.2692307692307692, 0.35897435897435903, 0.3974358974358974, 0.5256410256410257]
}

4. Bivar图&分箱调整

      画图观察每个变量(以单变量act_info为例)在开发样本和时间外样本上的Bivar图。

dev_slct2 = combiner.transform(dev_slct1)  # 根据节点实施分箱
val2 = combiner.transform(val[dev_slct1.columns])
off2 = combiner.transform(off[dev_slct1.columns])
# 分箱后通过画图观察  
from toad.plot import bin_plot, badrate_plot  
bin_plot(dev_slct2, x='act_info', target='label')  
bin_plot(val2, x='act_info', target='label')  
bin_plot(off2, x='act_info', target='label') 

      由于前3箱的变化趋势与整体不符(整体为递减趋势)，因此需将其合并(第4～6箱合并，最后3箱进行合并)，从而得到严格递减的变化趋势。

print(bins['act_info'])
# [0.115,0.141,...,0.525]
adj_bin = {'act_info': [0.166,0.3589,]}  
combiner.set_rules(adj_bin)
dev_slct3 = combiner.transform(dev_slct1)
val3 = combiner.transform(val[dev_slct1.columns])
off3 = combiner.transform(off[dev_slct1.columns])
# 画出Bivar图
bin_plot(dev_slct3, x='act_info', target='label')  
bin_plot(val3, x='act_info', target='label')  
bin_plot(off3, x='act_info', target='label') 

5. 绘制负样本占比关联图

data = pd.concat([dev_slct3,val3,off3], join='inner')   
badrate_plot(data, x='samp_type', target='label', by='act_info')  

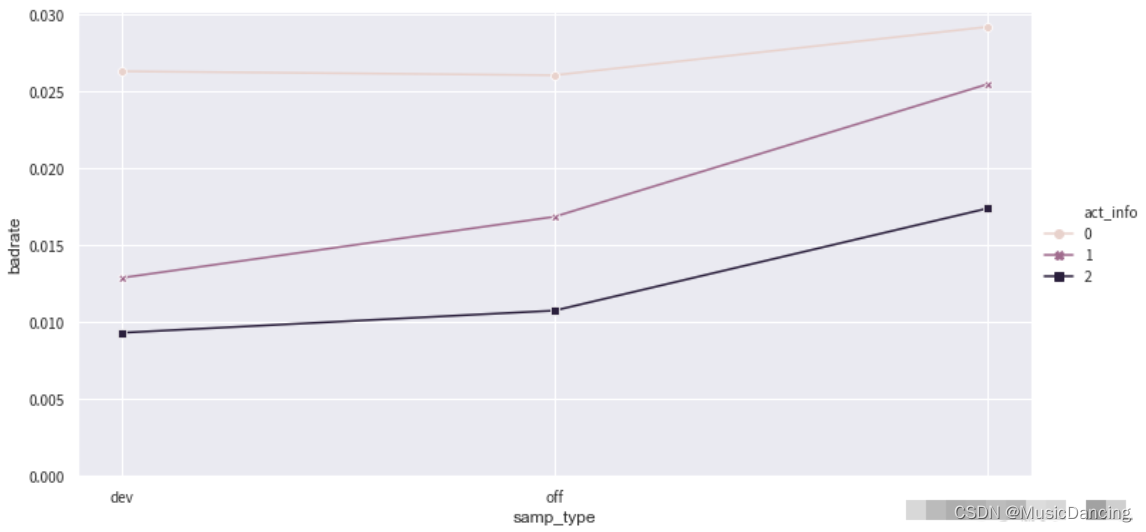
      图中的线没有交叉，不需要对该特征的分组进行合并，即使有少量交叉也不会对结果造成明显的影响，只有当错位比较严重的情况下才进行调整。

6. WOE编码,并验证IV

计算训练样本与测试样本的PSI

t = toad.transform.WOETransformer()  
dev_slct3_woe = t.fit_transform(dev_slct3, dev_slct3['label'], exclude=ex_lis) 
val_woe = t.transform(val3[dev_slct3.columns])  
off_woe = t.transform(off3[dev_slct3.columns])  
data = pd.concat([dev_slct3_woe, val_woe, off_woe])psi_df = toad.metrics.PSI(dev_slct3_woe, val_woe).sort_values(0)  
psi_df = psi_df.reset_index()  
psi_df = psi_df.rename(columns = {'index': 'feature', 0: 'psi'}) 
print(psi_df)

      删除PSI大于0.1的特征(通常单个特征的PSI值建议在0.1以下)，根据具体情况可以适当调整。

psi_013 = list(psi_df[psi_df.psi<0.1].feature) 
psi_013.extend(ex_lis)  # 避免不参与计算的几个特征被删掉，把uid,samp_type,label添加回来并去重
psi_013 = list(set(psi_013)) 
data = data[psi_013]    
dev_woe_psi, val_woe_psi, off_woe_psi = dev_slct3_woe[psi_013], val_woe[psi_013], off_woe[psi_013] 
print(data.shape)
# (95806, 11)

      卡方分箱后部分变量的IV降低，且整体相关程度增大，需要再次筛选特征。

dev_woe_psi2, drop_lst = toad.selection.select(dev_woe_psi,dev_woe_psi['label'], empty=0.6, iv=0.001, corr=0.5, return_drop=True, exclude=ex_lis)  
print("keep:", dev_woe_psi2.shape[1],  "drop empty:", len(drop_lst['empty']),  "drop iv:", len(drop_lst['iv']),  "drop corr:", len(drop_lst['corr'])) 

7. 特征筛选

       使用逐步回归进行特征筛选，使用线性回归模型，并选择KS作为评价指标

1. estimator: 用于拟合的模型，支持'ols', 'lr', 'lasso', 'ridge'；

2. direction: 逐步回归的方向，支持'forward', 'backward', 'both' (推荐)；

（1）Forward selection：

        将自变量逐个引入模型，引入一个自变量后查看该模型是否发生显著性变化，如果发生了显著性变化，那么则将该变量引入模型中，否则忽略该变量，直至遍历所有变量；即将变量按照贡献度从大到小排列，依次加入。

（2）Backward elimination：

        与Forward selection选择相反，将所有变量放入模型， 尝试将某一变量进行剔除，查看剔除后对整个模型是否有显著性变化，如没有显著性变化则剔除，有则保留，直到留下所有对模型有显著性变化的因素；也就是将自变量按贡献度从小到大，依次剔除。

（3）both：将前向选择与后向消除同时进行

        模型中每加入一个自变量，可能使某个已放入模型的变量显著性减小，显著性小于阈值时，可将该变量从模型中剔除；即每增加一个新的显著变量的同时，检验模型中所有变量的显著性，剔除不显著变量，从而得到最优变量组合。

3. criterion: 评判标准，支持'aic'、'bic'、'ks'、 'auc'；

4. max_iter: 最大循环次数；

5. return_drop: 是否返回被剔除的列名；

6. exclude: 不需要被训练的列名，比如ID列和时间列。

dev_woe_psi_stp = toad.selection.stepwise(dev_woe_psi2, dev_woe_psi2['label'], exclude=ex_lis, direction='both', criterion='ks', estimator='ols', intercept=False)  
val_woe_psi_stp = val_woe_psi[dev_woe_psi_stp.columns]  
off_woe_psi_stp = off_woe_psi[dev_woe_psi_stp.columns]  
data = pd.concat([dev_woe_psi_stp, val_woe_psi_stp, off_woe_psi_stp]) 
print(data.shape)
print(dev_woe_psi_stp.columns)  # 查看剩下的特征列

8. 模型训练

1. 模型训练及评估画图

def xgb_model(x, y, valx, valy, offx, offy, C):  # model = LogisticRegression(C=C, class_weight='balanced')  model = xgb.XGBClassifier(learning_rate=0.05, n_estimators=400,  max_depth=2, class_weight='balanced', min_child_weight=1,  subsample=1, nthread=-1, scale_pos_weight=1,  random_state=1, n_jobs=-1, reg_lambda=300)      model.fit(x,y)  y_pred = model.predict_proba(valx)[:,1]  fpr_val, tpr_val, _ = roc_curve(valy, y_pred)  val_ks = abs(fpr_val - tpr_val).max()  print('val_ks: ', val_ks)  from matplotlib import pyplot as plt  plt.plot(fpr_val, tpr_val, label='val')  plt.plot([0,1], [0,1], 'k--')  plt.xlabel('False positive rate')  plt.ylabel('True positive rate')  plt.title('ROC Curve')  plt.legend(loc='best')  plt.show() 

    2. 定义函数调用模型训练的方法

def bi_train(data, dep='label', exclude=None):  from sklearn.preprocessing import StandardScaler  std_scaler = StandardScaler()  lis = list(data.columns)  # 变量名  for i in exclude:  lis.remove(i)  data[lis] = std_scaler.fit_transform(data[lis])  devv = data[(data['samp_type']=='dev')] vall = data[(data['samp_type']=='val')] offf = data[(data['samp_type']=='off')]x, y = devv[lis], devv[dep]valx, valy = vall[lis], vall[dep]offx, offy = offf[lis], offf[dep]# XGBoost正向xgb_model(x, y, valx, valy, offx, offy) # XGBoost反向xgb_model(offx, offy, valx, valy, x, y)  

      正向调用通过对开发样本的学习得到模型，并在时间外样本上检验效果；逆向调用使用时间外样本作为训练集，检验当前模型的效果上限；如逆向模型训练集KS值明显小于正向模型训练集KS值，说明当前时间外样本分布与开发样本差异较大，需要重新划分样本集。(样本量较小时经常发生)

9. 模型评估

from toad.metrics import KS, F1, AUC 
prob_val = lr.predict_proba(valx)[:,1]  
print('跨时间')  
print('F1:', F1(prob_val,valy))  
print('KS:', KS(prob_val,valy))  
print('AUC:', AUC(prob_val,valy)) 
print('模型PSI: ', toad.metrics.PSI(prob_val, prob_val))  
print('特征PSI: ', toad.metrics.PSI(x, offx).sort_values(0))  

    生成模型时间外样本的KS报告 

toad.metrics.KS_bucket(prob_off, offy, bucket=15, method='quantile') 

    10. 生成评分卡

    将数据集合并后，利用ScoreCard函数重新训练并生成评分卡。

1. 参数 C 为'正则化强度'；

2. transer: 传入先前训练的 toad.WOETransformer 对象；

3. base_odds=20，base_score=750 实际意义为当比率为1/20，输出基准评分750，当比率为基准比率2倍时，基准分下降60分。

from toad.scorecard import ScoreCard  
card = ScoreCard(combiner=combiner, transer=t, C=0.1, class_weight='balanced',  base_score=600, base_odds=35, pdo=60, rate=2)  
card.fit(x,y)  
print(card.export(to_frame=True) )

 
 

         

这篇关于risk-jianmo整体流程梳理的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---