本文主要是介绍leetcode第 381 场周赛最后一题 差分,对称的处理,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
第 381 场周赛 - 力扣(LeetCode)最后一题3017. 按距离统计房屋对数目 II - 力扣(LeetCode)
dijkstra超时了,看了灵神的解题方法力扣(LeetCode)官网 - 全球极客挚爱的技术成长平台,其实是差分优化的暴力统计
灵神说的“撤销操作”,就是先不加那条xy新路,统计出所有距离对数,然后再加上那条路做修改。做修改需要推一下变短的位置。
灵神封装写的特别好,这道题不封装一下,有问题改起来很麻烦。
目录
统计原始距离对数:
找规律:
灵神暴力左右:
差分:
做修改:
第一种:
第二种:
关于小于区间右端点(x+y)/2:(等于过不了)
当 x==y 及x == y+1时没有缩短任何距离。不需要操作
参考代码:
统计原始距离对数:
这里说两种方法,第一种是自己想的找规律(其实踩坑了,没弄好差分),第二种就是灵神暴力,时间复杂度是相同的O(n)
找规律:
分别对奇数和偶数找一下:
第一行1 2 3 4 5五个数是题目里的房屋,左边第一列是距离 t,表中的则是与这个房屋距离为t的房屋数。
我们暴力完成这个表。
比如第一行,对1来说距离为1的只有2一个,所以是1;对2来说距离为1的是1和3,即两个。
会发现每一行会比前一行少2,而第一行也是“1 2 2 .. 2 2 1”可以列式算出来,所以可以距离为1到n的房屋对数数组(我们要返回的数组)给初始化。
// 1 2 3 4 5//1: 1 2 2 2 1 //2就算最多啦//2: 1 1 2 1 1 //-2//3: 1 1 0 1 1 //-2//4: 1 0 0 0 1 //-2//5: 0 0 0 0 0 //-2 这个要减成0// 1 2 3 4 5 6//1: 1 2 2 2 2 1//2: 1 1 2 2 1 1 //-2//3: 1 1 1 1 1 1 //-2//4: 1 1 0 0 1 1 //-2//5: 1 0 0 0 0 1 //-2//6: 0 0 0 0 0 0 //-2注意:
房屋数为n的情况下,不存在距离为n的房屋对(最大也是1和n之间差n-1),所以返回数组最后一位必定是0.
灵神暴力左右:
对于房屋 i ,距离为1的就是 i-1 和 i+1 ,距离为2的就是 i-2 和 i+2 ,......
一直到两边,可得左侧距离最大为i-1,右侧为n-i,
所以距离为 1 ~ i -1 的都要加一对,距离为 1 ~ n - i 的也都要加一对
差分:
而我们正好用的是差分数组。差分就是第一位为初始值,后面的都表示和前一位相差的值。对这种连续的情况,用差分是秒算的。
做修改:
首先看情况,其实就四种会变短,而这四种是对称的,也就是说其实就两种情况。
我们 i 为始点,j为终点,(x,y)为新增的路,我们让x<y。
第一种:
i 在 x左边 i <= x
只有当 j 在y左右的时候才会缩短距离:
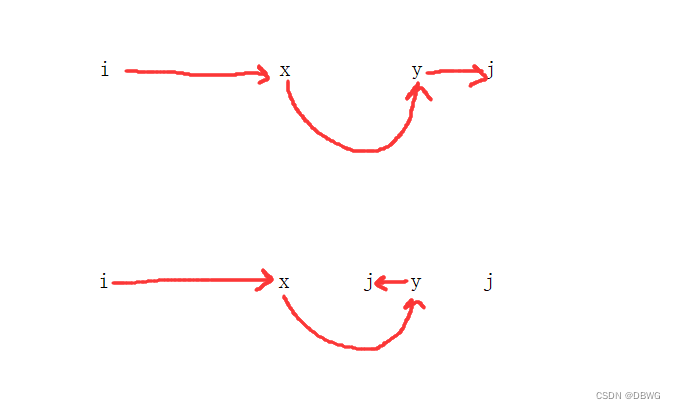
j在y左的位置的计算:就是算什么时候走新路更短

偶数的话会有一个点,这个点不走(大于号嘛,不取)
奇数的话本是两点之间,正好向下取整了,如下图的a,中间是正好,所以b可取
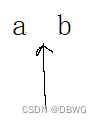
第二种:
x < i < (x+y)/2 剩下的区间就是对称的
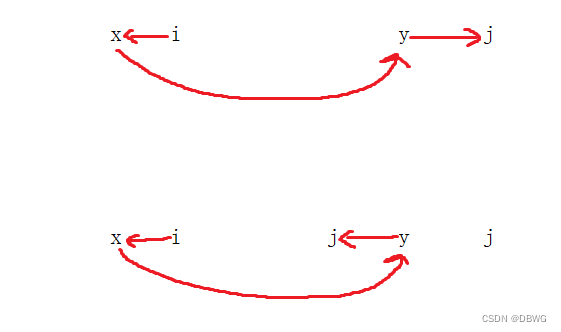
第二种的y左这个j的计算

关于小于区间右端点(x+y)/2:(等于过不了)
这个短点也没有缩短的:
奇数情况 x - - i - - y 很明显i到x和y一样远
偶数情况 x - i - - y i直接到y为3,i到x再到y为2+1 == 3
所以<(x+y)/2
——————
当 x==y 及x == y+1时没有缩短任何距离。不需要操作
参考代码:
灵神那个写的好,我没封装。不过对称的处理可以看看,处理是类似的。
他用函数会还原,我是用个if 还原的,然而if条件有关于对称用的值的,所以后面可能进不去,还原失败。
class Solution {
#define ll long longvector<ll>ans;void add(int l, int r, int v){if(l>r)return;ans[l] += v;ans[r + 1] -= v;}
public:vector<long long> countOfPairs(int n, int x, int y){if (x>y)swap(x, y);ans = vector<ll>(n + 2);// ans[1] = n + n - 2;// for (int i = 2; i <= n - 1; i++)// {// ans[i] = -2;// }//for (int k = 1; k <= n; k++){int i = k,orx = x,ory = y;add(1, i - 1, 1);add(1, n - i, 1);if (y - x < 2)continue;if (k > (orx + ory + 1) / 2){i = n + 1 - k;x = n + 1 - ory;y = n + 1 - orx;}if (i <= x){//1.j>=yadd(y - i, n - i,-1);//add(x-i+1,x-i+1+n-y, 1);没有想用“缩短的距离”int dec = y - x - 1;//比如 2 3 连完还是1,缩短了0,3-2-1add(y - i - dec, n - i - dec, 1);//2.x<j<y i x j y//只管能短的,即:j-i > x-i + 1 + y-j// 2j > x+y+1// j > (x+y+1)/2//j==(x+y+1)/2+1int j = (x + y + 1) / 2 + 1;//j到y-1add(j-i,y-i-1,-1);add(x - i + 2, x-i + 1 + y-j, 1);//3.j<=x不用管}else if (i < (x + y) / 2)// x - i - y 与 x - i - - y 都是不起作用,不需等于{ //等于的话//y右:add(y-i,n-i,-1);int dec = y - i - (i - x + 1);add(y - i-dec, n - i-dec, 1);//y左://j-i>i-x+1+y-j//2j>2i-x+1+y//j>(2i-x+1+y)/2int j = i + (- x + 1+ y) / 2 + 1;add(j-i,y-1-i,-1);add(i - x +2, i - x + y - j + 1,1);}if (k > (orx + ory + 1) / 2){x = orx;y = ory;}}vector<ll>ret(n);ll sum_d = 0;for (int i = 0; i < n; i++){sum_d += ans[i+1];ret[i] = sum_d;}return ret;}
};这篇关于leetcode第 381 场周赛最后一题 差分,对称的处理的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!






