【操作系统】银行家算法的实现

1 创作的小心思

该作旨在完成老师布置的实验任务，也借此机会系统的将银行家算法再学一遍。也可以蹭一波大家的热度，嘻嘻🤭，欢迎来访🎉🎉🎉

2 追根溯源

银行家算法（Banker’s Algorithm） 是一个避免死锁（Deadlock） 的著名算法，是由艾兹格·迪杰斯特拉在1965年为T.H.E系统设计的一种避免死锁产生的算法。它以银行借贷系统的分配策略为基础，判断并保证系统的安全运行。(来源：百度百科)

3 算法设计

3.1 银行家算法

3.1.1 所需维护的数据结构

1、可利用资源向量$Available$。这是一个含有$m$个元素的一维数组，其中的每一个元素代表一类可利用的资源数目，其初始值是系统中所配置的该类全部可用资源的数目，其数值随该类资源的分配和回收而动态的改变。若
$Available[j]=K$,则表示系统中现有 $R_j$ 类资源$K$ 个。

2、最大需求矩阵$Max$。这是一个 $n\times m$ 的矩阵，它定义了系统中$n$ 个进程中的每个进程对 $m$ 类资源的最大需求。若 $Max[i][j]=K$ ,则表示进程 $i$ 需要$R_j$ 类资源的最大数目为$K$ 。

3、分配矩阵$Allocation$。这是一个$n\times m$ 的矩阵，它定义了系统中每一类资源当前已分配给每一进程的资源数。若$Allocation[i][j]=K$ ,则表示进程 $i$ 当前已分得 $R_j$ 类资源的数目为 $K$ 。

4、需求矩阵$Need$。这是一个$n\times m$ 的矩阵，用以表示每一个进程尚需的各类资源数。若$Need[i][j]=K$ ,则表示进程$i$ 还需要$R_j$ 类资源$K$个方能完成其任务。

3.1.2 算法执行步骤

设$Request[i]$ 是进程$P_i$ 的请求向量， 如果$Request[i][j]=K$, 表示进程$P_i$ 需要$K$ 个$R_j$类型的资源。
当$P_i$ 发出资源请求后，系统按下述步骤进行检查：
(1)、如果$Request[i][j]\le Need[i][j]$,便转向步骤(2); 否则认为出错，因为它所需要的资源数已经超过它所宣布的最大值。
(2)、如果$Request[i][j]\le Available[j]$ ,便转向步骤(3); 否则，表示尚无足够资源，$P_i$ 须等待。
(3)、系统试探着把资源分配给进程$P_i$ ，并修改下面数据结构中的值：
$$\begin{gathered} Available[j]=Available[j]-Request[i][j] \\ Allocation[i][j]=Allocation[i][j]+Request[i][j] \\ Need[i][j]=Need[i][j]-Request[i][j] \end{gathered}$$
(4)、系统执行安全性算法，检查此次资源分配后系统是否处于安全状态。若安全，才正式将资源分配给进程$P_i$ ，以完成本次分配；否则，将本次试探分配作废，恢复原来资源分配状态，让进程$P_i$ 等待。

3.1.3 流程图

3.2 安全性算法

3.2.1 所需维护的数据结构

1、工作向量$Work$, 这是一个含有$m$ 个元素的一维数组，它表示系统可提供给进程继续运行所需的各类资源的数目，在执行安全算法开始时，$Work=Available$。（其实和$Available$ 所维护的内容一样）
2、进程状态向量$Finish$，这是一个含有$n$ 个元素的一维数组,它表示每一个进程是否运行完成，用布尔值来表示进程的状态，$Finish[i]=True$ 表示进程$P_i$ 已经运行完成，否则运行未完成。

3.2.2 算法执行步骤

(1) 从进程集合中找到一个能满足下述条件的进程：
①$Finish[i]=False$;
②$Need[i][j]\le Work[j]$;（注意：此处需要所有$m$ 类资源都满足该条件）
若找到，执行步骤(2)，否则，执行步骤(3)。
(2) 当进程$P_i$获得资源后，可顺利执行，直至完成，并释放出分配给它的资源：
$$\begin{gathered} Work[j]=Work[j]+Allocation[i][j]; \\ Finish[j]=True; \\ gotostep1; \end{gathered}$$
(4) 如果所有进程的Finish[i]=True都满足，则表示处于安全状态；否则，系统处于不安全状态。

3.2.3 流程图

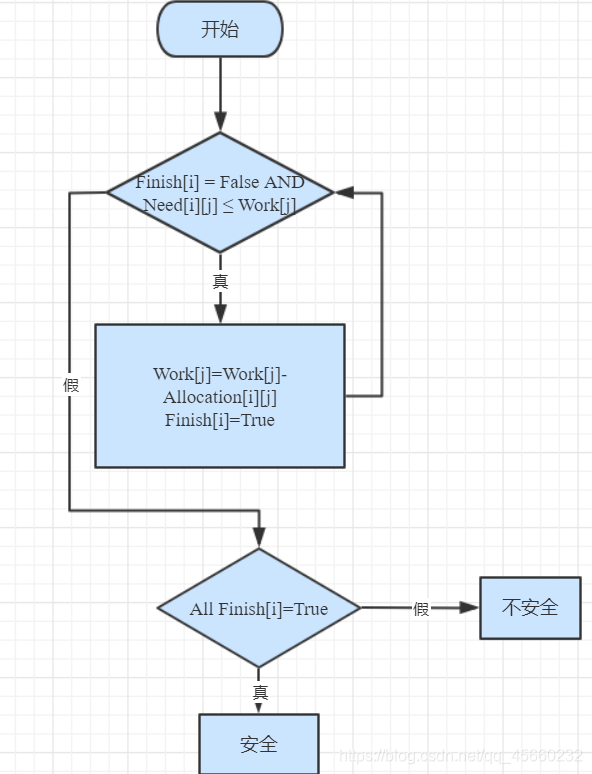
4 算法示例

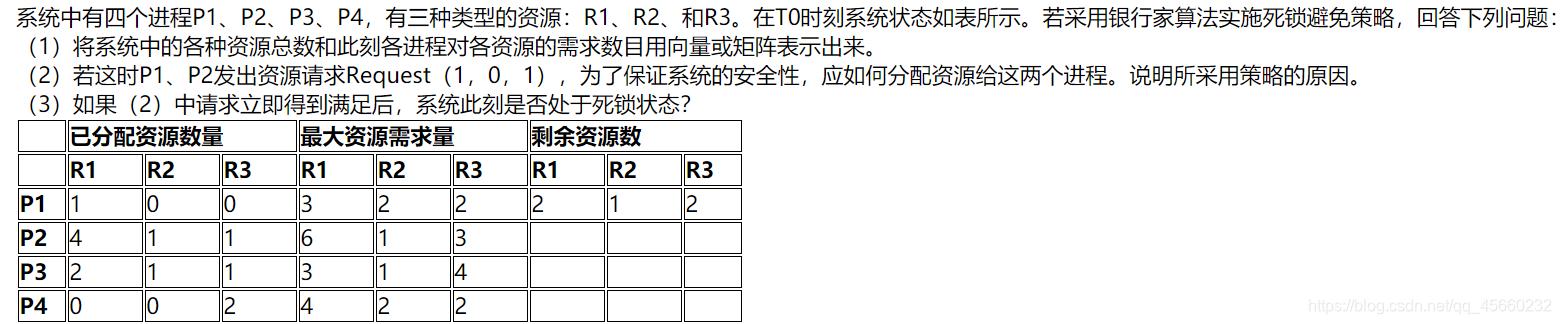
4.1 示例题目

4.2 例题求解

5 C++代码实现

5.1 C++源代码（全）

1.0版本，后续有时间了可能会再回来加强一波。请求资源方面，目前只能一次性分配一个，不能同时得到请求，需要改进，其他的基本功能算是实现了。执行过程的状态，比交好实现，加个输出就OK，比较简单，代码中就没实现。

#include<cstdio>
#include<queue>
#include<vector>
#include<stdlib.h>
#include<iostream>
#include<algorithm>
using namespace std;
const int N = 1010, M = 1010;
int n, m;
int Max[N][M], Allocation[N][M], Need[N][M];
int Available[M], Finish[N];
int Work[M], Request[M];
int Sum[M];//系统中m类资源的总量
void Init()
{cout << "请输入合法的矩阵" << endl;cout << "初始化Max矩阵" << endl;cout << "请输入一个" << n << "行" << m << "列的矩阵:" << endl;for (int i = 1;i <= n;i++)for (int j = 1;j <= m;j++)cin >> Max[i][j];cout << "初始化Allocation矩阵" << endl;cout << "请输入一个" << n << "行" << m << "列的矩阵:" << endl;for (int i = 1;i <= n;i++)for (int j = 1;j <= m;j++)cin >> Allocation[i][j];cout << "初始化Available向量" << endl;cout << "请输入一行" << m << "个元素表示当前可用资源的数量:" << endl;for (int i = 1;i <= m;i++) cin >> Available[i];/*初始化Need矩阵*/for (int i = 1;i <= n;i++){for (int j = 1;j <= m;j++){Need[i][j] = Max[i][j] - Allocation[i][j];}}/*初始化Sum矩阵*/for (int j = 1;j <= m;j++){for (int i = 1;i <= n;i++){Sum[j] += Allocation[i][j];}Sum[j] += Available[j];}cout << "初始化成功>^V^<" << endl;
}
/*判断初始化矩阵的合法性*/
bool Judge()
{for (int i = 1;i <= n;i++){for (int j = 1;j <= m;j++){if (Allocation[i][j] > Max[i][j]) return false;}}return true;
}
/*判断当前work向量是否大于Need[i]向量*/
bool Judge(int k)
{for (int j = 1;j <= m;j++){if (Need[k][j] > Work[j]) return false;}return true;
}
/*安全性检查的时候虚拟处理*/
void VirtureDeal(int k)
{for (int j = 1;j <= m;j++){Work[j] += Allocation[k][j];}Finish[k] = true;
}
/*安全性检查*/
bool SecurityCheck(queue<int>& q)
{memcpy(Work, Available, sizeof Available);memset(Finish, false, sizeof Finish);for(int k = 1;k <= n;k++) //n次迭代{bool flag = false;for (int i = 1;i <= n;i++){if (!Finish[i] && Judge(i)){flag = true;q.push(i);VirtureDeal(i);break;}}if (!flag) return false;}return true;
}
/*试探性分配资源*/
void Alloc(int k)
{for (int j = 1;j <= m;j++){Allocation[k][j] += Request[j];Need[k][j] -= Request[j];Available[j] -= Request[j];}
}
/*恢复原状*/
void Recover(int k)
{for (int j = 1;j <= m;j++){Allocation[k][j] -= Request[j];Need[k][j] += Request[j];Available[j] += Request[j];}
}
/*请求资源*/
void Query()
{int ID;cout << "请输入进程ID(1 -- " << n << "):" << endl; cin >> ID;cout << "请输入请求向量(输入" << m << "个有效整数):" << endl;for (int j = 1;j <= m;j++) cin >> Request[j];for (int j = 1;j <= m;j++){if (Request[j] > Need[ID][j]){cout << "出错，请求的资源大于需求资源" << endl;return;}else if (Request[j] > Available[j]){cout << "进程无法得到资源，继续处于等待状态！" << endl;return;}}Alloc(ID);//试探性分配queue<int> q;if (SecurityCheck(q)){cout << "分配资源成功！" << endl;cout << "其中的一个安全序列是：";bool mark = false;while (q.size()){if (mark) cout << "->";cout << q.front();q.pop();mark = true;}cout << endl;}else {cout << "无法执行分配任务！" << endl;Recover(ID);//无法执行分配，恢复原状}
}
int main()
{cout << "请输入进程个数: "; cin >> n;cout << "请输入资源的种类数: "; cin >> m;Init();system("pause");while (1){system("cls");cout << "1、请求资源" << endl;cout << "2、检查当前状态的安全性" << endl;cout << "0、退出主程序" << endl;while (1){int op; cin >> op;if (op < 0 || op > 2) {cout << "操做错误，请重新输入！！！" << endl;system("pause");}else {if (op == 0) exit(0);else if (op == 1) {Query();system("pause");}else if (op == 2){queue<int> q;if (SecurityCheck(q)){cout << "当前状态安全" << endl;cout << "其中的一个安全序列是：";bool mark = false;while (q.size()){if (mark) cout << "->";cout << q.front();q.pop();mark = true;}cout << endl;}else {cout << "当前状态不安全，极有可能进入死锁状态" << endl;}system("pause");}}break;}}return 0;
}
/*
Max
3 2 2
6 1 3
3 1 4
4 2 2
Allocation
1 0 0
4 1 1
2 1 1
0 0 2
Available
2 1 2
*/

5.2 测试截图

5.2.1 初始化

5.2.2 进程1发出资源请求（1，0，1）

5.2.3 进程2发出资源请求（1，0，1）

5.2.4 检查当前状态安全性

欢迎大家在评论区提出自己的疑问，我会在评论区进行回复。
也欢迎批评我写的不足之处，能力范围之内我会进行加强，我们一起共勉👊。