算法 - 插入排序（Insertion Sort）

本文主要是介绍算法 - 插入排序（Insertion Sort），希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

插入排序非常类似于扑克牌的排序
执行流程

在执行过程中，插入排序会将序列分为2部分（头部是已经排好序的，尾部是待排序的）
从头开始扫描每一个元素（每当扫描到一个元素，就将它插入到头部适合的位置，使得头部数据依然保持有序）

void sort() {for (int begin = 1; begin < array.length; begin++) {int cur = begin;while (cur > 0 && cmp(cur, cur - 1) < 0) {swap(cur, cur - 1);cur--;}}
}

逆序对（Inversion）

什么是逆序对？
数组<2, 3, 8, 6, 1>的逆序对为：<2, 1> < 3, 1> <8, 1> <8, 6> <6, 1>，共5个逆序对
插入排序的时间复杂度与逆序对的数量成正比关系
逆序对的数量越多，插入排序的时间复杂度越高
最坏、平均时间复杂度：O(n²)
最好的时间复杂度：O(n)
空间复杂度：O(1)
属于稳定排序
当逆序对的数量极少时，插入排序的效率特别高
甚至速度比O(nlogn)级别的快速排序还要快
数量不是特别大的时候，插入排序的效率也是非常好的

插入排序优化1

思路是将「交换」转为「挪动」

先将待插入的元素备份
头部有序数据中比待插入元素大的，都朝尾部方向挪动1个位置
将待插入元素放到最终的合适位置

for (int begin = 1; begin < array.length; begin++) {int cur = begin;T v = array[cur];while (cur > 0 && cmp(v, array[cur - 1]) < 0) {array[cur] = array[cur - 1];cur--;}array[cur] = v;
}

二分搜索（Binary Search）

如何确定一个元素在数组中的位置？（假设数组里面全都是整数）

如果是无序数组，从第0个位置开始遍历搜索，平均时间复杂度：O(n)
在这里插入图片描述
如果是有序数组，可以使用二分搜索，最坏时间复杂度：O(logn)

二分搜索 - 思路

假设在[begin, end)范围内搜索某个元素v，mid == (begin + end) / 2
如果 v < m，去[begin, mid) 范围内二分搜索
如果 v > m，去[mid + 1, end)范围内二分搜索
如果 v == m，直接返回mid

二分搜索 - 实例

在这里插入图片描述

查找v在有序数组array中的位置

public static int search(int[] array, int v) {if (array == null || array.length == 0) return -1;int begin = 0;int end = array.length;while (begin < end) {int mid = (begin + end) >> 1;if (v < array[mid]) {end = mid;} else if (v > array[mid]) {begin = mid + 1;} else {return mid;}}return -1;
}

思考

如果存在多个重复的值，返回的是哪一个？
不确定

二分搜索优化

在元素v的插入过程中，可以先二分搜索出合适的插入位置，然后再将元素v插入
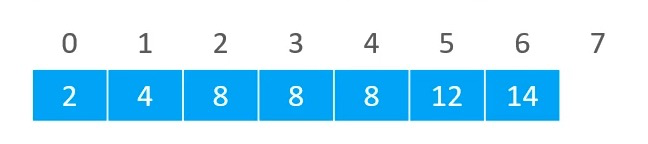
要求二分搜索返回的插入位置：第1个大于v的元素位置

如果v是5，返回2
如果v是1，返回0
如果v是15，返回7
如果v是8，返回5

查找v在有序数组array中的插入位置

public static int search(int[] array, int v) {int begin = 0;int end = index;while (begin < end) {int mid = (begin + end) >> 1;if (cmp(array[index], array[mid]) < 0) {end = mid;} else {begin = mid + 1;}}return begin;
}

插入排序最终版本：

public int[] sort(int[] array) {for (int begin = 1; begin < array.length; begin++) {insert(array, begin, search(array, begin));}
}
/*** 将source位置的元素插入到dest位置* @param source* @param dest*/
private void insert(int[] array, int source, int dest) {int v = array[source];for (int i = source; i > dest; i--) {array[i] = array[i - 1];}array[dest] = v;
}/*** 利用二分搜索找到 index 位置元素的待插入位置* 已经排好序数组的区间范围是 [0, index)* @param index* @return*/
private int search(int[] array, int index) {int begin = 0;int end = index;while (begin < end) {int mid = (begin + end) >> 1;if (cmp(array[index], array[mid]) < 0) {end = mid;} else {begin = mid + 1;}}return begin;
}