CNN——NormLayer（BN、FRN）的学习笔记~

本文主要是介绍CNN——NormLayer（BN、FRN）的学习笔记~，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

1 致谢

感谢网友wzy_zju提供的资料，链接如下：
https://blog.csdn.net/wzy_zju/article/details/81262453

2 前言

今天在学习CNN~
我之前一直对BN的作用还不是很明白，所以今天再来复习一下~
首先我们来看看关于 norm layer 的经典示意图

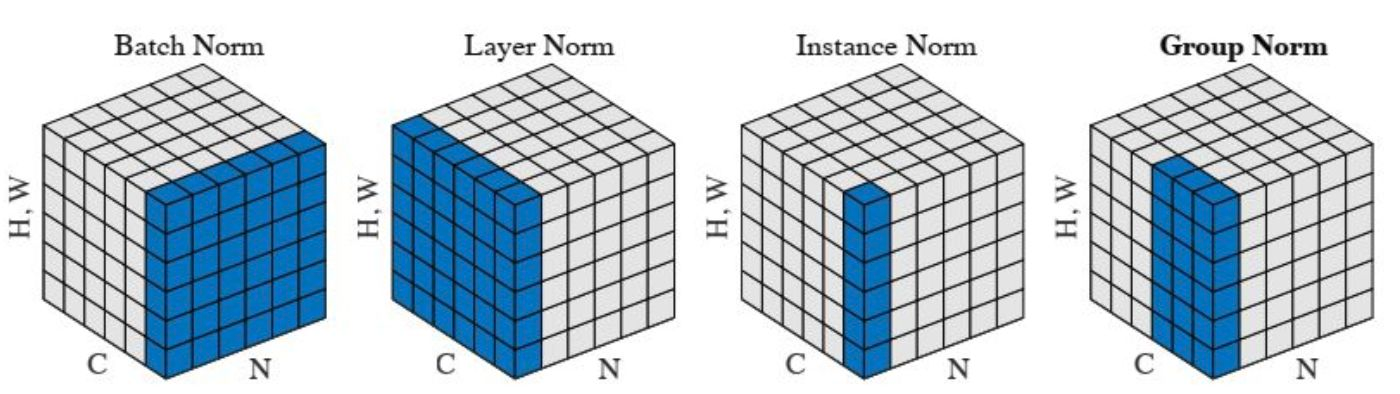
3 BN：Batch Normalization

3.1 BN所解决的问题

其实BN的效果跟图像归一化的效果是类似的，都是为了解决特征数值归一化的问题；

3.2 Batch Normalization的算法思路

这里我们可以参考一下原始论文的算法图：

$\gamma \gamma$：可学习参数，缩放因子；
$\beta \beta$：可学习参数，平移因子；
（这里“可学习参数”的意思是，这里的$\gamma$和$\beta$会跟其它权值一样参加BP的计算，也就是一个“普通的权值”）

3.3 BN的非线性

BN是一个非线性算子；
算子：算子是一个函数空间到函数空间上的映射$O:X\to Y$。
下面我们对BN层的非线性进行说明，这里采用一个简单的方法进行论证，BN层其实包含了两个算子操作：归一化算子和线性算子$\gamma x+\beta$，
易知，线性算子$\gamma x+\beta$必然是线性的；
这里我们将第一层运算${\hat{x}}_i\leftarrow \frac{x_i-{\mu }_{\mathcal{B}}}{\sqrt{{\sigma }_{\mathcal{B}}^2+ϵ}}$看作是归一化操作，$ϵ$为数值稳定项，在理论推导时看作$0$；
下面我们对归一化算子的非线性进行证明：
首先，看看线性算子的定义，线性算子需满足以下性质，设$X$和$Y$是两个线性空间，$T$是$X$到$Y$的映射，
$$T(\alpha x_1+\beta x_2)=\alpha T\left(x_1\right)+\beta T\left(x_2\right)$$
等价于同时满足以下两个性质

• 可加性：$T(x_1+x_2)=T\left(x_1\right)+T\left(x_2\right)$
• 齐次性：$T(k{x}_1)=kT\left(x_1\right)$

现在证明归一化算子$N$不满足齐次性，
归一化算子的公式如下
$$N(x)=\frac{x-D(x)}{\sigma \left(x\right)}$$
则有
$$\begin{array}{rl}N(ax)& =\frac{ax-D(ax)}{\sigma \left(ax\right)}\\ & =\frac{ax-a\cdot D(x)}{a\cdot \sigma \left(x\right)}\\ & =\frac{x-\cdot D(x)}{\sigma \left(x\right)}\\ & =N\left(x\right)\end{array}$$
不满足第二个性质，
$\therefore$归一化算子是非线性算子。

nn.BatchNorm2d()

BatchNorm2d包含以下五个内部参数：

• weight：可学习权值参数，对应$\gamma$；
• bias：可学习偏置参数，对应$\beta$；
• running_mean：持久参数，记录分布的均值，对应$\text{E}[x]$
• running_var：持久参数，记录分布的方差，对应$\text{Var}[x]$
• num_batches_tracked

4 MABN——“BN variant”

MABN论文：Towards Stabilizing Batch Statistics in Backward Propagation of Batch Normalization
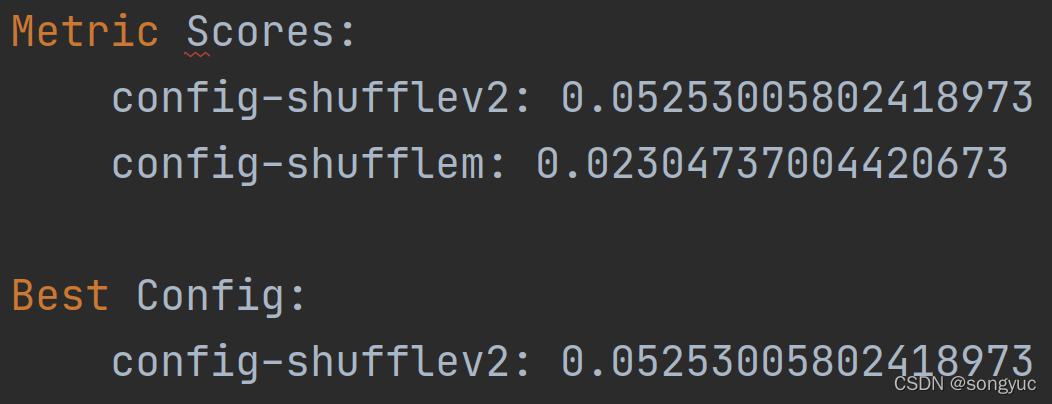
备注：在ShuffleNetv2中试了一下MABN，实验没有效果，

5 FRN (Filter Response Normalization)

FRN是我在知乎上面看到的norm-layer，感觉还是有点帅的；
这里记录一下FRN的torch实现：

• 《超越BatchNorm你不可不知的两种方案：FRN与MABN》——给出的FRN的代码实现
• 《深度学习5种标准化层BN、GN、LN、IN、SN + 谷歌提出新的标准化层：FRN》——从图像归一化和标准化的角度来理解BN的作用

6 NormLayer的归一化代码理解

关于NormLayer的分布归一化的实现理解，请参考《PyTorch45——五种归一化的原理与代码逐行实现(BatchNorm/LayerNorm/InsNorm/GroupNorm/WeightNorm)》；
这个教程使用PyTorch的计算函数验证了各种NormLayer的分布归一化的操作；

7 NormLayer类的继承关系

.: `Module` 
|--> `_NormBase`: norm-layer的基类
|  |--> `_BatchNorm`: BatchNorm层的基类  
| |-- components：组件代码，包括：HomePage  
| |-- file 
|-- examples.desktop  
|-- file  

这篇关于CNN——NormLayer（BN、FRN）的学习笔记~的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---