本文主要是介绍漫漫数学之旅008,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
文章目录
- 经典格言
- 数学习题
- 古今评注
- 名人小传
- (一)莫扎特
- (二)赫拉克利特

经典格言
如果我们不期望着意外,那么我们永远找不到意外。——赫拉克利特(Heraclitus)
赫拉克利特的这句名言“如果我们不期望着意外,那么我们永远找不到意外”,揭示了一种深刻的人生哲理和宇宙观。这句话可以从两个层面来理解:
首先,从认知和生活态度的角度看,赫拉克利特鼓励人们保持开放、好奇与接纳的心态。如果我们在生活中总是按部就班,只做自己认为熟悉和预期的事情,不愿意接受未知和不确定性,那么我们就可能错过许多意想不到的机会和体验。意外往往蕴藏着新的知识、见解和成长,它能打破常规,带来创新和突破。只有勇于面对并期待未知,才能真正拥抱生活中的各种意外,并从中获益。
其次,从哲学和自然规律层面讲,赫拉克利特强调了变化是世界的本质。在他看来,万物都在永恒地流动和变化之中,不变的就是变化本身(“Panta Rhei”)。这里的“意外”可以被理解为自然世界中无时无刻不在发生的变数和不可预见性。若我们固守已知和旧有的观念,无法适应和理解这种普遍存在的变化,那就无法洞察到世界的真实面貌,更无法在不断涌现的“意外”中找到推动社会进步和个人发展的力量。
因此,赫拉克利特提醒我们要以积极而开放的态度去期待和接纳生活中的“意外”,并在不断变化的世界中发现和创造价值。
数学习题
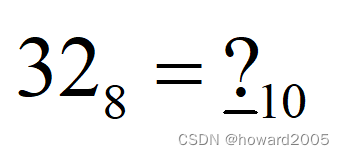
古今评注
你是否曾幻想过,只需听一首曲子,就能瞬间化身数学小天才,解决那些复杂的几何难题?这听起来就像魔法,但在科研的世界里,它似乎真的存在——至少对于莫扎特的D大调双钢琴奏鸣曲(K.448)来说,确实有那么点儿神奇的效果。
加州大学欧文分校的一群研究者们进行了一项饶有趣味的研究。他们找来一群学生,不是让他们苦哈哈地刷题库,而是请他们在轻松愉快的氛围下聆听十分钟莫扎特的这首经典之作。结果呢?这些原本可能还在和数学公式斗智斗勇的学生们,在时空推理测试中的智商得分竟然噌噌噌地上升了!这让不少人大跌眼镜:原来音乐也能成为数学思维的“脑力助推器”!
这究竟是怎么一回事呢?科学家们给出的一种解释是,莫扎特的音乐如同一位优雅的神经导体,通过其精妙复杂的结构与和谐旋律,能够激活大脑中与数学思考相关的神经网络,让这些区域之间的连接变得更加紧密且活跃。换言之,或许在欣赏莫扎特奏鸣曲的过程中,你的大脑正在悄无声息地进行一场提升逻辑思维、增强空间感知的“瑜伽锻炼”。
不仅如此,这位奥地利音乐大师的作品还被发现具有超乎艺术范畴的治疗效果。据说,K.448奏鸣曲对癫痫患者的病情缓解以及阿尔兹海默病人的时空推理能力改善也有着积极的影响。试想一下,如果有一天医生给你开的处方上赫然写着:“每日聆听莫扎特D大调双钢琴奏鸣曲10分钟”,那画面是不是既奇特又充满幽默感?
总而言之,虽然我们不能指望仅凭一曲莫扎特就变成数学大神,但音乐的力量的确能潜移默化地影响我们的认知功能。所以,下次当你在面对数学难题感到头疼时,不妨试试先放点莫扎特的音乐,没准儿它会帮你打开一个全新的思考维度,让你在优美的旋律中找到解开谜题的灵感钥匙。而这一切,都要归功于那个古典音乐界的小顽童——莫扎特和他的神奇奏鸣曲。
名人小传
(一)莫扎特
莫扎特,这位音乐界的“小鬼才”,要是生活在今天,估计会是各大社交媒体的流量担当,不仅因为他天赋异禀,更因为他身上那股子幽默劲儿和顽皮气质。想象一下他活跃在Instagram上,一边晒出自己刚出炉的新作,一边调侃:“嘿,朋友们,我刚刚又创作了一部交响曲,速度之快,比你们刷抖音还快!”
莫扎特从小就展现了惊人的音乐才华,大概三岁就能谱曲,五岁就开始欧洲巡演,这要搁现在,绝对是儿童版的“我是歌手”。每次演出结束,观众们无不惊叹:“哎呀妈呀,这是哪来的神仙小孩儿?!”而我们的小莫扎特则眨巴着大眼睛,一脸天真无邪地说:“我只是把听到的所有声音都串成了歌儿。”
他的作品风格多样,从深沉厚重到轻盈欢快,无所不能。据说有一次,他为了证明自己的创作速度,边打牌边写了一首交响曲,就像我们如今边追剧边发朋友圈一样轻松。如果当时有直播平台,标题一定是:“看我如何在打完一副牌的时间里完成一部交响曲!”
莫扎特生活中的幽默也不乏趣事,比如他喜欢给朋友起昵称,其中最著名的可能是对海顿的称呼——“爸爸海顿”,既体现了他对前辈的尊重,也透着一股子亲切和俏皮。若是在现代,他可能就是那个热衷于给人取绰号、活跃气氛的团队开心果。
此外,莫扎特对于音乐的热爱与执着让他即使生活困顿,依然坚持创作。如果他在微博上感慨,大概会这样写道:“穷得只能吃泡面,但灵感却如满汉全席般丰盛。毕竟,人生如歌,总得有个让人惊艳的副歌部分,不是吗?”
总之,莫扎特用他的音乐才华和乐观态度,为后世留下了一段充满笑声和乐符的人生故事。他是古典音乐界的一股清流,也是我们心中那个永远年轻、永远快乐、永远才华横溢的“音乐顽童”。
(二)赫拉克利特
赫拉克利特,这位古希腊哲学界的“段子手”,如果生活在现代,大概率会是个微博上的热门博主,因为他的人生和观点都充满了幽默与哲理的火花。想象一下,他头戴哲学家的光环,却用着脱口秀主持人的腔调跟你聊宇宙、火与万物变化。
首先,我们得说说他的身世。要是放在今天,赫拉克利特可能是出身名门的贵公子,但他可没打算继承王位,毕竟他是以弗所国王赫拉克勒德斯的儿子。你可能会想,“嘿,那家伙放着国王不当,跑去研究哲学?”是的,他就这么任性,仿佛在说:“当国王?那多无趣!我更乐意做生命的探索者,寻找那个永恒不变的真理——变。”这小子估计是在思考:世界是流动不息的一场大火,而你们却在争抢一把暂时的权杖?
据说,赫拉克利特拒绝了王冠,选择了去山上过起了隐士生活。他大概心里琢磨:“皇宫里哪有山洞安静?在那里,我可以一边烤火(象征万物皆火),一边领悟万物皆流的道理。”想象一下他在社交媒体上更新状态:“今日感悟:水能载舟亦能煮粥,人能为王亦能为智者,关键在于选择自己的河流。”
他还留下了一句传世经典:“人不能两次踏入同一条河流。”这句话要是放到当今社会,就是:“别以为你在朋友圈发同样角度的自拍就算创新,河水它都不允许你重复昨天的自己!”真是让人忍俊不禁又深思不已。
赫拉克利特不仅喜欢大自然里的篝火晚会,还特别善于冷嘲热讽那些他认为浅薄无知的人们。他说:“多数人甚至连听都没听说过智慧,少数人刚听说就忘掉了,只有极少数人才能理解和实践。”翻译成现代网络语言,大概就是:“大部分网友刷到知识贴瞬间就滑走,少部分收藏后从未回顾,唯有寥寥数人真的学以致用。”
所以,如果你有幸穿越回古希腊,碰到这位既幽默又深刻的赫拉克利特,估计会被他犀利又富含哲理的俏皮话给逗乐的同时,也被深深地启发和教育一番。他的人生就像他自己所说的那样:“一切都在变化,不变的是变化本身。”也许在他看来,无论是哲学还是幽默,都是生命之火燃烧出的不同颜色的火焰吧。
这篇关于漫漫数学之旅008的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!







