漫漫数学之旅007

本文主要是介绍漫漫数学之旅007，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

经典格言

如果我们能想象一个足够伟大的意识，知道宇宙当前时刻一切物体的准确位置和速度，还有所受的一切外力，那么，宇宙对这个意识就毫无秘密可言。这个意识，能够根据因果律推算出过去或将来的一切事情。——皮埃尔·西蒙·拉普拉斯（Pierre-Simon de Laplace）

数学习题

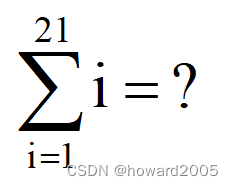
古今评注

让我们穿越时空，聚焦在印度璀璨的数学与天文学历史中，一本名为《增订婆罗门历数全书》（Brahma Sphuta Siddhanta）的伟大著作映入眼帘。该书由杰出的古印度天文学家和数学家婆罗门笈多（Bhramagupta，公元598-665年）倾力编撰，它不仅涵盖了深邃丰富的天文学理论，更包含了一系列奠定现代数学基石的重要思想。

在这部堪称百科全书式的天文历算学巨著中，婆罗门笈多对零和负数的概念进行了开创性的探讨，并首次系统地阐述了零、正数以及负数之间的算术运算法则。他明确提出了零作为一个独立数字存在的意义，这一概念在当时是革命性的突破，对于数学乃至整个科学领域的发展都产生了深远的影响。

尤为值得一提的是，婆罗门笈多在书中关于二次方程的研究令人叹为观止。他揭示了二次方程可以拥有两个实根的事实，这一发现早于欧洲数学界近一千年。在他的解析下，二次方程不再是一个无法解开的秘密，而是成为了一种可计算、可预测的数学工具，极大地推动了代数学的发展进程。

综上所述，《增订婆罗门历数全书》不仅是一本详尽的天文学指南，更是人类数学智慧的瑰宝，婆罗门笈多凭借其卓越的洞察力和创新精神，在这部作品中播下了影响后世数学及天文学发展的种子，展现了一个古代科学家无与伦比的才智与远见。

数学家小传

（一）婆罗门笈多

在遥远的古代印度，繁星璀璨的夜空下，诞生了一位闪耀着智慧光芒的天文学家与数学家——婆罗门笈多（Bhramagupta）。公元598年，他呱呱坠地于数学与哲学思想交汇激荡的土地上，仿佛预示着他将为人类知识宝库增添一份独特而宝贵的财富。

婆罗门笈多自幼便展现出对数字和天文现象的异乎寻常的兴趣，他的世界就如同一个巨大的算盘和无垠的宇宙，等待着被探索、被计算。这位“天空的诗人”，用几何和代数的语言描绘星辰轨迹，用严谨的逻辑揭开宇宙的秘密。

时光流转至公元628年，婆罗门笈多完成了他的巨著《增订婆罗门历数全书》。这本书宛如一颗横空出世的智慧流星，照亮了当时乃至后世数学和天文学的道路。在这部作品中，他不仅详述了复杂的天文观测方法和计算规则，还首次系统地阐述了零和负数的概念以及它们之间的运算规律，如同在数学的荒原上栽种了一片茂密的森林。

更令人惊叹的是，婆罗门笈多还揭示了二次方程可能有两个解这一革命性发现，这个秘密直到千年之后才被欧洲数学家所普遍认知。这就好比他在时间的长河中埋藏了一个宝藏，耐心等待着后来者的发掘与传承。

婆罗门笈多的一生，就像一段传奇的故事，充满了对知识的热忱追求与卓越贡献。他的名字镌刻在历史的星空之上，提醒着世人：无论是遥不可及的星辰大海，还是看似平淡无奇的阿拉伯数字，都隐藏着无穷的魅力与深邃的智慧，等待着我们去探索、去创造。

（二）皮埃尔·西蒙·拉普拉斯

皮埃尔·西蒙·拉普拉斯，这位科学界的法式传奇，就像一部精密的天文钟，以其精准无误的计算和对宇宙奥秘的不懈探索，敲响了18世纪末至19世纪初物理学与天文学的高潮乐章。他出生于1749年法国一个名叫博蒙昂诺日的小村庄，仿佛一颗未被发掘的星辰，从一开始就注定要在浩渺星海中熠熠生辉。

拉普拉斯的智慧犹如满载星辰的夜空，深邃且迷人。他的“恶魔”理论堪称科幻与哲学交织的经典——设想存在一个智能生物能够掌握宇宙中所有粒子的位置和速度，那么这个“恶魔”就能预测整个宇宙的未来走向，这一观点被誉为"拉普拉斯妖"，在后世引发了关于决定论与自由意志的深刻讨论。

他在数学物理领域的贡献更是璀璨夺目，提出的拉普拉斯变换至今仍是解决许多工程、物理问题的重要工具。而他的《天体力学》一书，则像是为牛顿引力定律谱写的交响诗，构建了一个宏大而严谨的天体运动体系，使他被誉为“天体力学之父”。

生活中，拉普拉斯以低调内敛著称，他的世界似乎没有不可解的谜团，只有等待揭示的规律。他曾是拿破仑的御用科学家，但面对权力的诱惑，他更醉心于科研的广阔天地。他的存在就是一种证明：科学的魅力在于其揭示宇宙秩序的力量，而杰出的科学家，正是那些能驾驭这种力量、点亮人类认知边界的人。

总之，皮埃尔·西蒙·拉普拉斯，这位活跃于启蒙时代的巨人，以他对数学、天文学的独特洞察力和无尽的好奇心，编织了一幅跨越时空、直指宇宙深处的宏伟画卷，成为科学史上永恒闪耀的一颗巨星。

这篇关于漫漫数学之旅007的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---