本文主要是介绍校招必考:根据二叉树遍历序列确定二叉树,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
根据二叉树的前序遍历和中序遍历求其后序遍历或者根据二叉树的后序遍历和中序遍历求其前序遍历是腾讯等校招的必考题,下面我们就来分析一下解题思路。
这道题本质上是要我们根据二叉树遍历序列确定二叉树,只要二叉树确定了,求它的任何遍历序列都是易如反掌的。
理论基础:
由二叉树的先序遍历序列(PreorderTraverse)和中序遍历序列(InorderTraverse)或由其后序遍历序列(PostorderTraverse)和中序遍历序列均能唯一地确定一棵二叉树。
求解过程:
1. 先序序列第一个结点一定是二叉树的根节点 。
2. 根节点在中序序列中必然将中序序列分割为两个子序列,前一个序列为根节点的左子树的中序序列,后一个序列为根节点的右子树的中序序列。
3. 递归使用以上两条法则,直到序列只剩下一个结点。
如果是后序序列和中序序列,那么步骤1改为后序序列的最后一个结点一定是二叉树的根结点。
例:已知结点的先序序列和中序序列分别为:
先序序列:18 14 7 3 11 22 35 27
中序序列:3 7 11 14 18 22 27 35
则可按上述分解求得整棵二叉树。
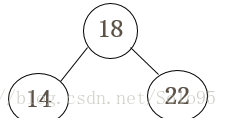
- 18为根结点 中序序列分割为 3 7 11 14 18 22 27 35 左右两部分 18的左子树是14 右子树是22。
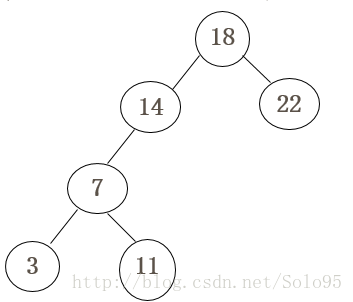
- 左边3 7 11 14中,14是根,3 7 11都在其左边,因此都是14的左子树,14没有右子树。
- 再由先序序列18 14 7 3 11得, 7是14的左子树。
- 左边3 7 11, 7 是根,3在7左边即为其左子树,11在7右边即为其右子树,左边推导完毕。
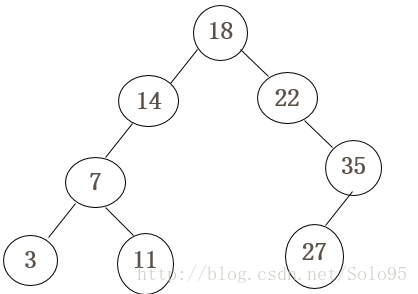
- 右边22 24 35,则24、35都是22的右子树。
- 再看前序序列22 35 27, 35是22的左子树与上面矛盾,则22没有左子树,35是22的右子树
右边 24 35,24在35左边则为其左子树,右边推导完毕。二叉树已经能够确定。
- 现在你能求出这棵二叉树的后序遍历吗?
作者注:
推导过程中序遍历是依据,先找根,找到根以后,根左边都是其右左子树,右边都是其右子树。中序和前序遍历出现矛盾以中序为准,说明这个根下面可能只有右子树。
每个结点都是一个根,所以推导任何一个结点的方法都相同(递归就是反复调用同一个方法)。
二叉树遍历是递归进行的,所以我们才能通过递归的方法反向推导整棵树。
这篇关于校招必考:根据二叉树遍历序列确定二叉树的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!