牛客周赛 Round 12 解题报告 | 珂学家 | 异或拆位技巧+加权前缀和

贪心，即第一天就施肥，

然后3天形成一个循环节, y + 3 * x

然后需要处理下尾巴

import java.io.BufferedInputStream;
import java.util.Scanner;public class Main {public static void main(String[] args) {Scanner sc = new Scanner(new BufferedInputStream(System.in));long x = sc.nextLong(), y = sc.nextInt(), z = sc.nextInt();long round = y + 3 * x;if (z % round == 0) {System.out.println(z / round * 3);} else {long r = z / round * 3;long left = z % round;if (left > 0) {r += 1; // 第一天(x+y)r += (Math.max(left - y - x, 0) + x - 1) / x;}System.out.println(r);}}}

双指针寻求匹配即可

import java.io.BufferedInputStream;
import java.util.Scanner;public class Main {public static void main(String[] args) {Scanner sc = new Scanner(new BufferedInputStream(System.in));int h = sc.nextInt(), w = sc.nextInt();char[][] grid = new char[h][];for (int i = 0; i < h; i++) {grid[i] = sc.next().toCharArray();}char[] p = "meituan".toCharArray();int k = 0;for (int i = 0; i < h; i++) {for (int j = 0; j < w; j++) {if (k < p.length && grid[i][j] == p[k]) {// 在一行中找到了匹配字符k++;break;}}}System.out.println(k >= p.length ? "YES" : "NO");}}

贪心，要使得最后的元素和最大，那一定要使得单个元素最大

挑选最大的最多k个数（都大于1），然后累加剩下的数

import java.io.*;
import java.util.*;public class Main {public static void main(String[] args) {Scanner sc = new Scanner(new BufferedInputStream(System.in));int n = sc.nextInt(), k = sc.nextInt();int[] arr = new int[n];for (int i = 0; i < n; i++) {arr[i] = sc.nextInt();}Arrays.sort(arr);long mod = 10_0000_0007l;long res = 1l;// 挑选最大的k个数int t = Math.min(k + 1, n - 1);for (int i = 0; i < t; i++) {res = res * arr[n - 1 - i] % mod;}// 合并后产生的1res = ((res + (t - 1)) % mod + mod) % mod;// n-k个剩余的数for (int i = t; i < n; i++) {res = (res + arr[n - 1 - i]) % mod;}System.out.println(res);}}

先来解决下一个简单的前置问题

求一个集合S中所有任意两元素的异或和

关于这个问题，相对比较简单，就是拆位，按30个二进制位进行统计，分别统计0和1的个数，根据异或性质

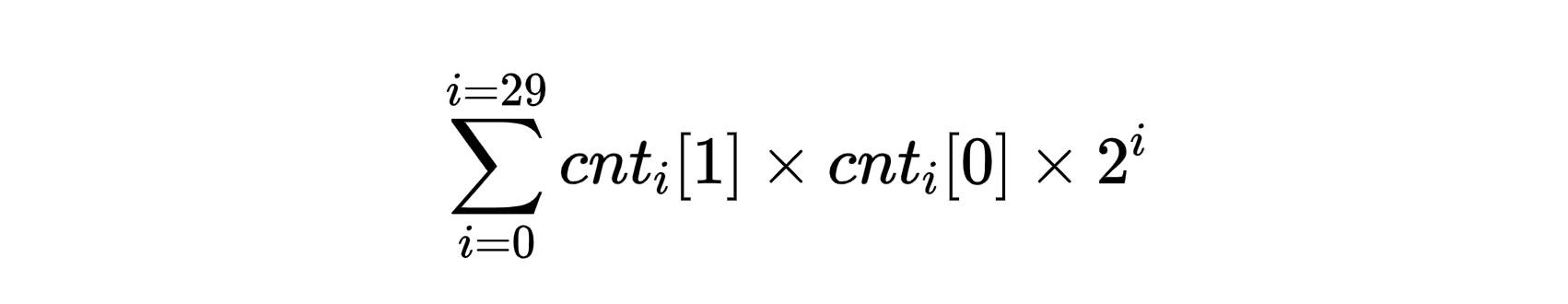
在回到本题，这题需要求解

所有连续子数组的 异或和

如果枚举所有的子数组，就算前缀和优化，时间复杂度依然达到 $O(n^2),n=10^5$

所以需要看看，如何降维

令$S_i$为以第i元素为右端点的所有区间(集合)的异或和

现在问题，就是如何优化下括号这块

异或和不满足分配律，且很难维护，但是拆位后就很容易了

• 拆位+加权前缀和

$a_i(j)$表示第i个元素第j位的值，$[a_t(j)=x]$相等为1,不等为0

定义p(i, j, x)表示前i个元素，在二进制的j位，等于x的加权前缀和

简单来说，就是 加权$i$ (下标位置) 按位维护0,1的前缀加权和。

到这，基本这题就结束了。

import java.io.*;
import java.util.*;public class Main {public static void main(String[] args) {Scanner sc = new Scanner(new BufferedInputStream(System.in));int n = sc.nextInt();int[] arr = new int[n];for (int i = 0; i < n; i++) {arr[i] = sc.nextInt();}// 拆位// 0, 1的个数long mod = 10_0000_0007l;long[][] pre = new long[30][2];long[] s = new long[n + 1];for (int i = 0; i < n; i++) {long delta = 0;for (int j = 0; j < 30; j++) {if (((1 << j) & arr[i]) != 0) {delta = (delta + pre[j][0] * (1l << j) % mod) % mod;} else {delta = (delta + pre[j][1] * (1l << j) % mod) % mod;}}// s(i+1)=s(i)+增量s[i + 1] = (s[i] + delta) % mod;for (int j = 0; j < 30; j++) {if (((1 << j) & arr[i]) != 0) {// 加权体现在(i+1)上pre[j][1] = (pre[j][1] + (i + 1)) % mod;} else {pre[j][0] = (pre[j][0] + (i + 1)) % mod;}}}// 累加和long res = 0;for (int i = 1; i <= n; i++) {res = (res + s[i]) % mod;}System.out.println(res);}}