本文主要是介绍TN Tutorial(0-1):建立量子态,演化门实例等,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
本节是注解搭建ADQC必要的基础模块:

* 初始化量子态:Library.QuantumState.TensorPureState ( ) 要传参建立实例,MF只能建立参数
(1)Psi = TensorPureState( psi_ ):psi_作为一个 2**num_qbits 交由MF建立的参数张量
psi_ = qs.state_all_up( n_qubits = 3,d = 2) 返回一个|000>态
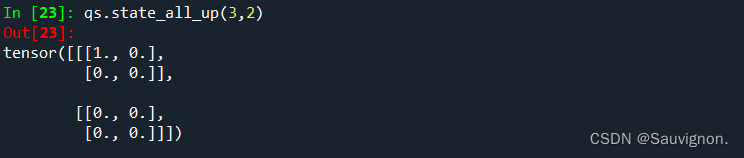
psi_ = qs.state_ghz( n_qubit = 3) 返回一个 态
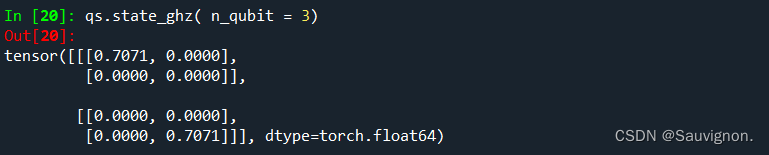
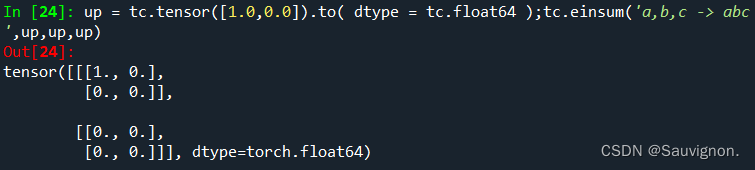
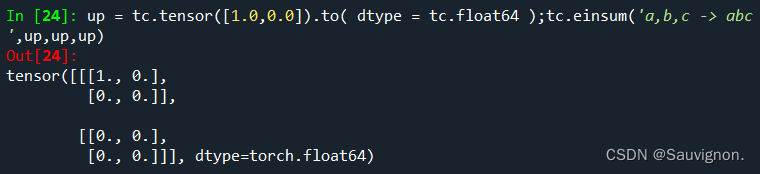
up = tc.tensor([1.0,0.0]).to( dtype = tc.float64 ) + psi_ = tc.einsum('a,b,c -> abc ',up,up,up)
(2)Psi = TensorPureState( nq = 4 )随机建立态,以及如果有机会你会看到后面ADQC会在 建立一个随机目标态psi_target(只作为计算保真度的部分并不参与线路演化) 我们对比一下:
Psi: 梦开始的地方|000》
Psi:nq=4 的 TensorPureState( )
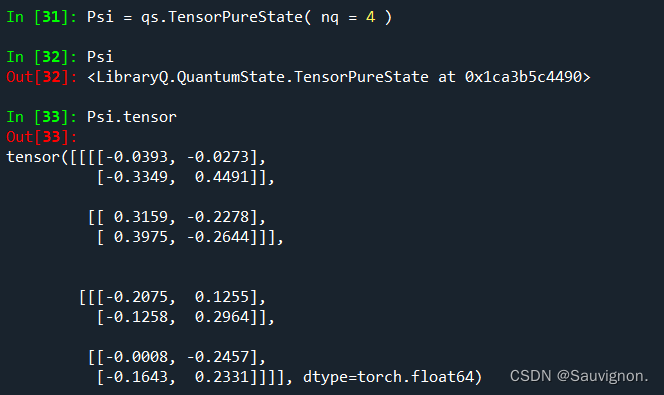
返回一个一长串高阶张量,conj( ).flatten( ),获得可以拿去点积的平展形式

这简直就是psi_target:
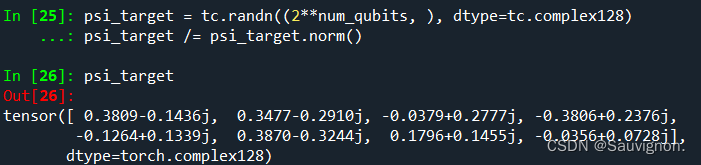
* 定义门:建立了Psi 实例后,MathFun可以提供演化门的细节
(1)mf.pauli_operators( ), mf.swap( ), mf.hadamard( ), mf.phase_shift( ):QFT_3的手写例子
print('初态为|000>')
up = tc.tensor([1.0, 0.0]).to(dtype=tc.float64)
psi = TensorPureState(tc.einsum('a,b,c->abc', up, up, up))psi.act_single_gate(mf.hadamard(), [0])
psi.act_single_gate(mf.phase_shift(pi/2), [0], [1])
psi.act_single_gate(mf.phase_shift(pi/4), [0], [2])
psi.act_single_gate(mf.hadamard(), [1])
psi.act_single_gate(mf.phase_shift(pi/2), [1], [2])
psi.act_single_gate(mf.hadamard(), [2])(2)Psi.act_single_gate( ) StaeOP.py传4*4矩阵,内置函数细节可以转换为2*2*2*2的张量:
psi0_ = ghz.clone()
psi0 = qs.TensorPureState(psi0_)cnot = tc.tensor([[1, 0, 0, 0], [0, 1, 0, 0],[0, 0, 0, 1], [0, 0, 1, 0]]).to(dtype=tc.float64)print('在量子位1(控制)与2(目标)上作用矩阵上传的CNOT后得:')
psi1.act_single_gate(cnot, [1, 2])
print(psi1.tensor.flatten())print('在量子位1(控制)与2(目标)上作用2*2*2*2张量上传的CNOT后得:')
psi0.act_single_gate(cnot.reshape(2,2,2,2), [1, 2])
print(psi1.tensor.flatten())psi0 ~ psi1原理在于:act_single_gate类函数l56-l68里有reshape,转成合乎多体演化的多阶张量
for pp in pos_control:perm.remove(pp)perm = pos + perm + pos_controlstate1 = self.tensor.permute(perm).reshape(2 ** m_p, -1, 2 ** m_c)state1_ = state1[:, :, :-1]state2_ = gate.reshape(-1, 2 ** m_p).mm(state1[:, :, -1])state1 = tc.cat([state1_, state2_.reshape(state2_.shape + (1,))], dim=-1)(3)ADGate 那章有模块化编程之后细讲:

有了模块化编程就豁然开朗,如果说前面都是教学工具的话,开发到这一步到这一步才像 vqnet,qiskit_learning等专业框架一样,真上道了。。。。orz.
* 量子态演化:act_single_gate(gate,cqbit1,cqbit2) 方法(1,2 制备均匀叠加态)
(1)Psi.act_single_gate( ), 插入门演化量子态的直接方法
U.append(mf.hadamard())psi_ = qs.state_all_up(4, 2).to(dtype=tc.float64)
Psi = qs.TensorPureState(psi_)
Psi.act_single_gate(U[0],[0])
Psi.act_single_gate(U[0],[1])
Psi.act_single_gate(U[0],[2])
Psi.act_single_gate(U[0],[3])
(2)Psi.observation( gate,[qbit_nth] ), 直接获取该位置的期望值

(3)Psi.reduced_density_matrix( ), 获取该位置约化密度矩阵进行svdvals后获得纠缠谱
* 这是一个对 nq=4 的 4-qubits 随机态的采样,详见rmd_sample.py
![]()
原理上要获得(2,3)间的纠缠谱:permute(1,2,0,3)再reshape(4,4),并且与自己点积
print('求[1,2]位置对应的约化密度矩阵')
psi = TensorPureState(nq=4) # 4-qubit随机量子态
rmd1 = psi.reduced_density_matrix([1, 2])tmp = psi.tensor.permute(1, 2, 0, 3).reshape(4, 4)
rmd2 = tmp.mm(tmp.t())
print('两种方法结果的差 = ', (rmd1 - rmd2).norm().item())值得一提的约化密度矩阵的原理与张量的向量化: 
之后的张量网络收缩里我们也有这个矩阵化,规则人话说就是把指标分成两组各自将指标向量化(abc...)x(ABCD...)把各元素的访问索引返回成一个矩阵:所谓向量化,是指返回一个向量, 依原tensor指标先后次序, 将元素索引一 一访问后获得的线性排布。
(4)Psi.sampling( 2048 , [3] ), 跟随qbits[3],随机采样2048次,获得结果分布
![]()
(5)Psi.bipartite_ent([0,1])纠缠谱,与其它几个谱方法的比较:
* Psi返回的奇异谱:
s0 = svdvals(psi.tensor.reshape(4, 4))
print('SVD获得的奇异值:\n', s0)* Psi约化矩阵返回的本征谱:
rho = psi.reduced_density_matrix([2, 3])
s1 = eigvalsh(rho)
print('约化矩阵rho[2,3]的本征值(开方):\n',sqrt(s1.sort(descending=True)[0]))* Psi约化矩阵成员函数的二分纠缠谱:
print('调用成员函数获得的本征谱:\n',psi.bipartite_ent([0, 1]))
纠缠谱,纠缠熵:纠缠熵作为纠缠谱的平方的概率分布,算纠缠熵,刻画了两个子体系之间的纠缠大小;此外,不同的二分方式确定了不同的奇异谱或纠缠谱的计算方式,体现在对量子态系数 的矩阵化。纠缠谱平方本质上也是对应约化密度矩阵的本征谱。

* 量子态演化:act_N_qubit_QFT(psi)方法
(1)原理:
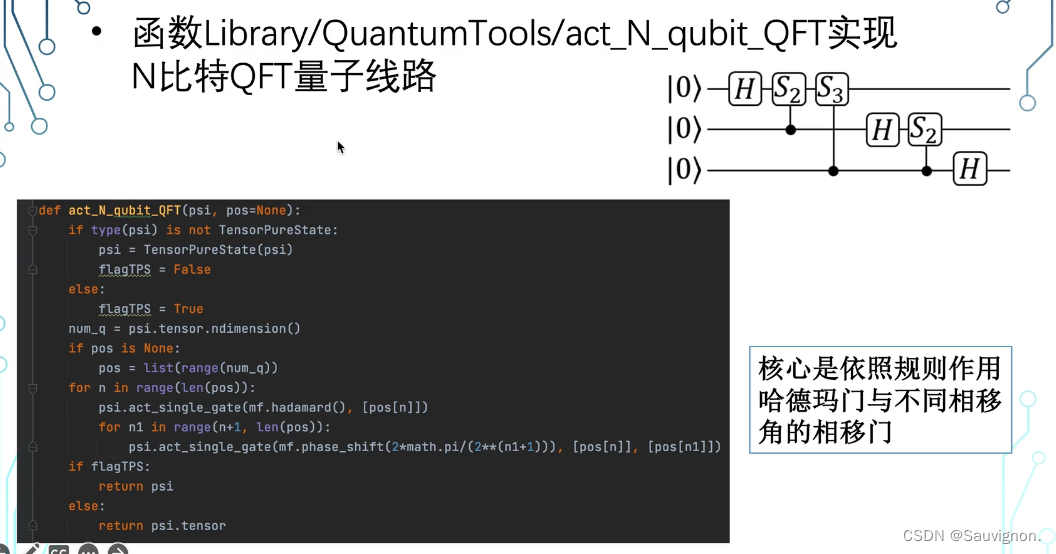
(2)规则与运行:
* 毕竟是一组门实例的封装的,可以指定qbit_nth对psi进行局部qft
* 在pos送入一个list装载待qft的qbits
#对|0000> 0,1,2号位进行QFT:
psi_test = TensorPureState(tc.einsum('a,b,c,d->abcd',up,up,up,up))
psi_test = act_N_qubit_QFT(psi_test,pos = [0,1,2])
#对|0000> 0,1,3号位进行QFT:
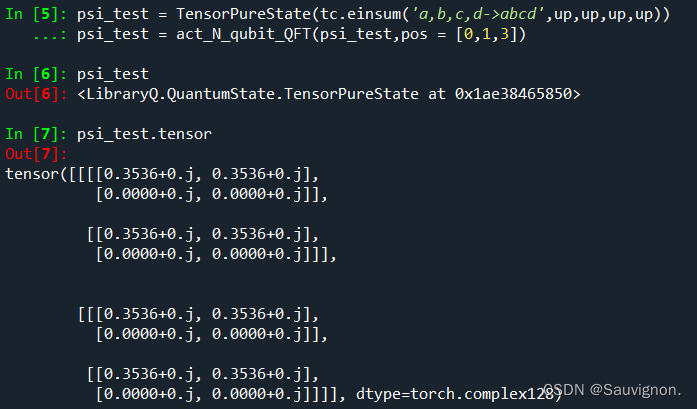
psi_test = TensorPureState(tc.einsum('a,b,c,d->abcd',up,up,up,up))
psi_test = act_N_qubit_QFT(psi_test,pos = [0,1,3])* 表示一下对psi[0,1,2],psi[0,1,3],进行的QFT编码
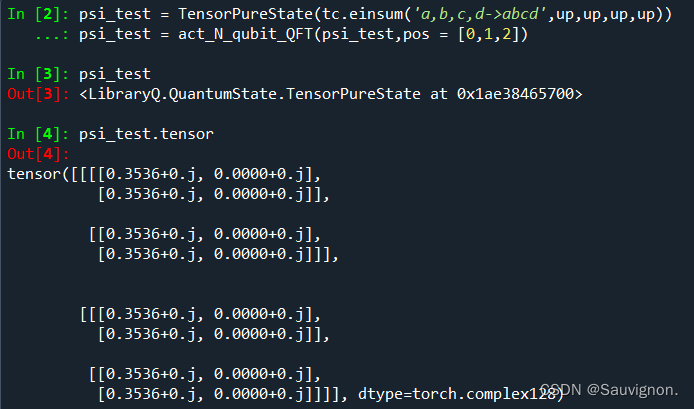
* 建立并运行一个完整的量子线路实例,我们就是把它分成以上三个部分来完成的:(1)建立量子态实例psi;(2)演化量子线路,psi.act_single_gate或者是psi.act_N_qubits_QFT ;(3)psi的测量与运行结果的处理。
这篇关于TN Tutorial(0-1):建立量子态,演化门实例等的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!





