第45届ICPC昆明刷题

比赛传送门

传送门

A-AC

题面

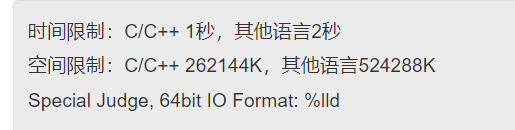
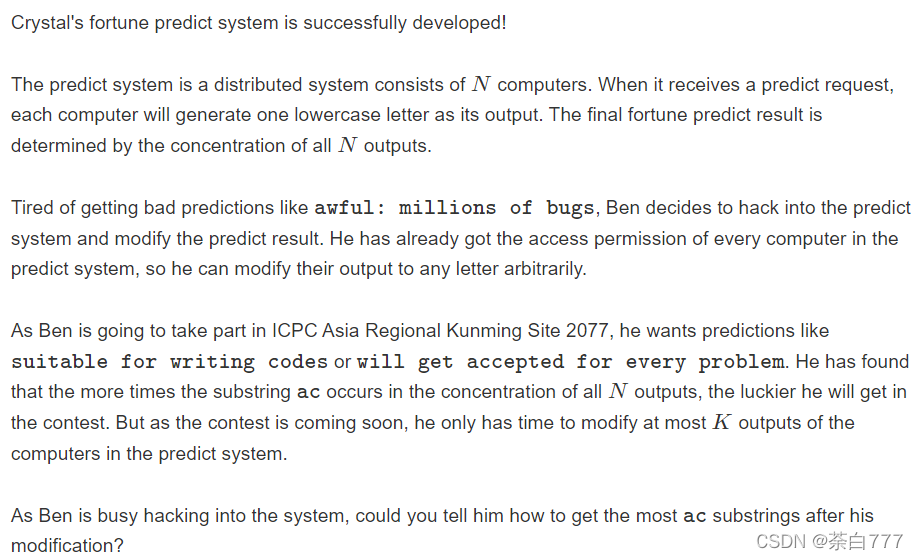
思路

首先我们不考虑输出解决方案，只考虑输出有几个ac；

令str(i) = 'a'，str(i+1) = 'c'，所需要的代价是a[i]；

那么不难想到，如果我们选择了a[i]，那么a[i-1]与a[i+1]是不能选的；

也就是说问题变成了在花费不超过k的情况下，最多可以选择多少个互不相邻的位置i；

---

那么假设我们已经选择了a[i]，现在我们想要反悔选择a[i-1]与a[i+1]；

那么我们可以按照下面这种方式来反悔；

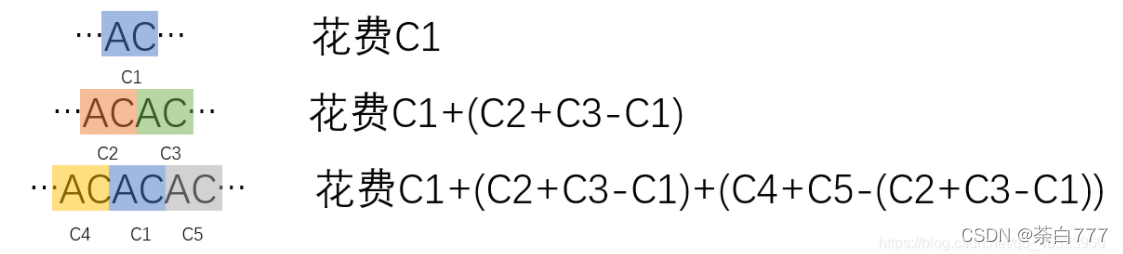
那么这个过程我们使用小根堆来完成；

然后具体解决方案的输出，我们再多维护两个数组l[i]与r[i]，表示$(l,r]$已经被ac覆盖了；

Code

#include <iostream>
#include <cstring>
#include <cstdio>
#include <algorithm>
#include <utility>
#include <numeric>
#include <vector>
#include <queue>using namespace std;typedef long long ll;const int N = 5e5 + 10;char str[N];
int n,k,pre[N],nxt[N];
int l[N],r[N],a[N];
typedef pair<int,int> pii;
priority_queue<pii,vector<pii>,greater<pii>> pq;
bool del[N];
void solve(){cin >> n >> k;cin >> (str+1);for(int i=1;i<=n;++i){nxt[i] = i + 1;pre[i] = i - 1;l[i] = r[i] = i;}for(int i=1;i<n;++i){a[i] = (str[i] != 'a') + (str[i+1] != 'c');pq.push({a[i],i});}a[0] = a[n] = 1e9;//非法状态int ans = 0;while(!pq.empty()){auto u = pq.top();int id = u.second,val = u.first;pq.pop();if(val > k) break;if(del[id]) continue;//选择当前这个点k -= val,++ans;//反悔a[id] = a[pre[id]] + a[nxt[id]] - val;//扩展当前点l[id] = l[pre[id]],r[id] = r[nxt[id]];del[pre[id]] = del[nxt[id]] = 1;//类似链表的操作pre[id] = pre[pre[id]],nxt[id] = nxt[nxt[id]];pre[nxt[id]] = id,nxt[pre[id]] = id;pq.push({a[id],id});}cout << ans << '\n';for(int i=1;i<=n-1;++i){if(del[i]) continue;for(int j=l[i]+1;j<=r[i];++j){str[j] = 'a',str[++j] = 'c';}}cout << (str+1);
}signed main(){std::ios::sync_with_stdio(false),cin.tie(0),cout.tie(0);solve();return 0;
}

G-Gift

题面

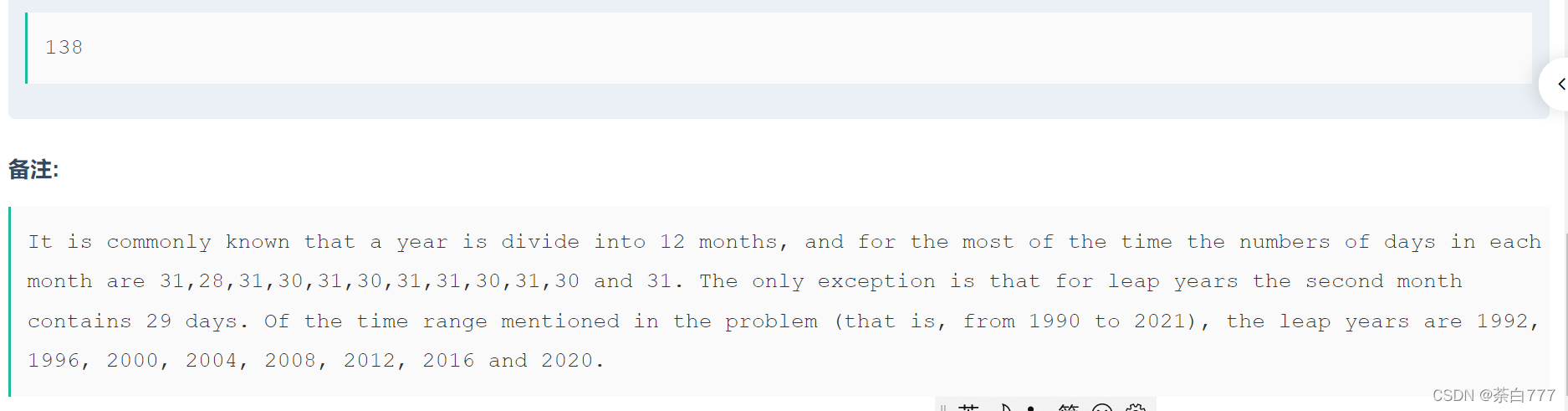
思路

首先有一个坑，2021年的2月是没有29号滴；

---

归纳一下题意，我们对于每个朋友可以有三种选择；

• 不搭理他
• 给他做蛋糕
• 送他礼物

不难发现，礼物与做蛋糕是可以独立开来的；

我们首先考虑礼物；

因为礼物数量很少(至多15)，我们可以考虑暴力枚举(选或不选)来完成，花费时间为$O(2^M)$，当然也可以用DP来解决；

接着假设只有做蛋糕，没有送礼物这一说；

$f(i,j)表示前i个人，做cake不超过j天得到的最大价值$

这不就是一个经典的0-1背包吗？

接着我们引入礼物；

$f(i,j,k)表示前i个人，做cake不超过j天，给k个人送gift所得到的最大价值$

状态方程也不难想到，就按照上面说的，忽略/送蛋糕/送礼物来转移即可；

$f[i][j][k]=f[i-1][j][k]，忽略$
$f[i][j][k]=f[i-1][j-w][k]+v，送蛋糕$
$f[i][j][k]=f[i-1][j][k-1])，送礼物$

最后加一个常见的滚动数组优化一维度即可；

(不搞也行)

Code

#include <iostream>
#include <cstring>
#include <string>
#include <vector>
#include <cstdio>
#include <algorithm>using namespace std;typedef long long ll;const int N = 1e5 + 10;
int months[] = {0,31,28,31,30,31,30,31,31,30,31,30,31};
int gmx[20];
struct Friend{int dist_day,w,v;bool operator<(const Friend& o) const{return dist_day < o.dist_day;}
};
int change(string date){//yyyy-dd-mm//5,6,8,9int month = ((date[5] - '0') * 10) + (date[6] - '0');int day = ((date[8] - '0') * 10) + (date[9] - '0');int ret = day;for(int i=1;i<month;++i) ret += months[i];return ret;
}
int n,m,money,w[20],v[20];
void init_gifts(){memset(gmx,0,sizeof gmx);for(int i=1;i<=m;++i){cin >> w[i] >> v[i];}for(int s = 1;s < (1 << m);++s){//依次看看买了哪几个int spend = 0,val = 0,cnt = 0;for(int j=1;j<=m;++j){if(s & (1 << (j-1))){spend += w[j];val += v[j];++cnt;}	}if(spend <= money){gmx[cnt] = max(gmx[cnt],val);}}//买的多不一定好，取一个max前缀for(int i=1;i<=m;++i)gmx[i] = max(gmx[i],gmx[i-1]);
}
//f(i,j,k)表示前i个人，做cake不超过j天
//给k个人送gift所得到的最大价值
int f[2][370][20];
vector<Friend> friends;
int dp(){memset(f,-0x3f,sizeof f);for(int j=0;j<=365;++j)f[0 & 1][j][0] = 0;int ret = 0;for(int i=1;i<=n;++i){auto &ff = friends[i-1];int birth = ff.dist_day,w = ff.w,v = ff.v;for(int j=0;j<=365;++j){for(int k=0;k<=m;++k){//忽略f[i & 1][j][k] = f[(i-1) & 1][j][k];//做cakeif(j >= w && birth >= j)f[i & 1][j][k] = max(f[i & 1][j][k],f[(i-1) & 1][j-w][k]+v);//送giftif(k > 0)f[i & 1][j][k] = max(f[i & 1][j][k],f[(i-1) & 1][j][k-1]);ret = max(ret,f[i & 1][j][k] + gmx[k]);}}}return ret;
}
void solve(){friends.clear();cin >> n >> m >> money;int t = 0;for(int i=1;i<=n;++i){string date;int w,v;//花费，价值cin >> date >> w >> v;if(date[5] == '0' && date[6] == '2' && date[8] == '2' && date[9] == '9'){++t;continue;}friends.push_back({change(date),w,v});}n -= t;sort(friends.begin(),friends.end());init_gifts();cout << dp() << '\n';	
}signed main(){std::ios::sync_with_stdio(false),cin.tie(0),cout.tie(0);int t;cin >> t;while(t--)solve();return 0;
}

M - Stone Games

题面

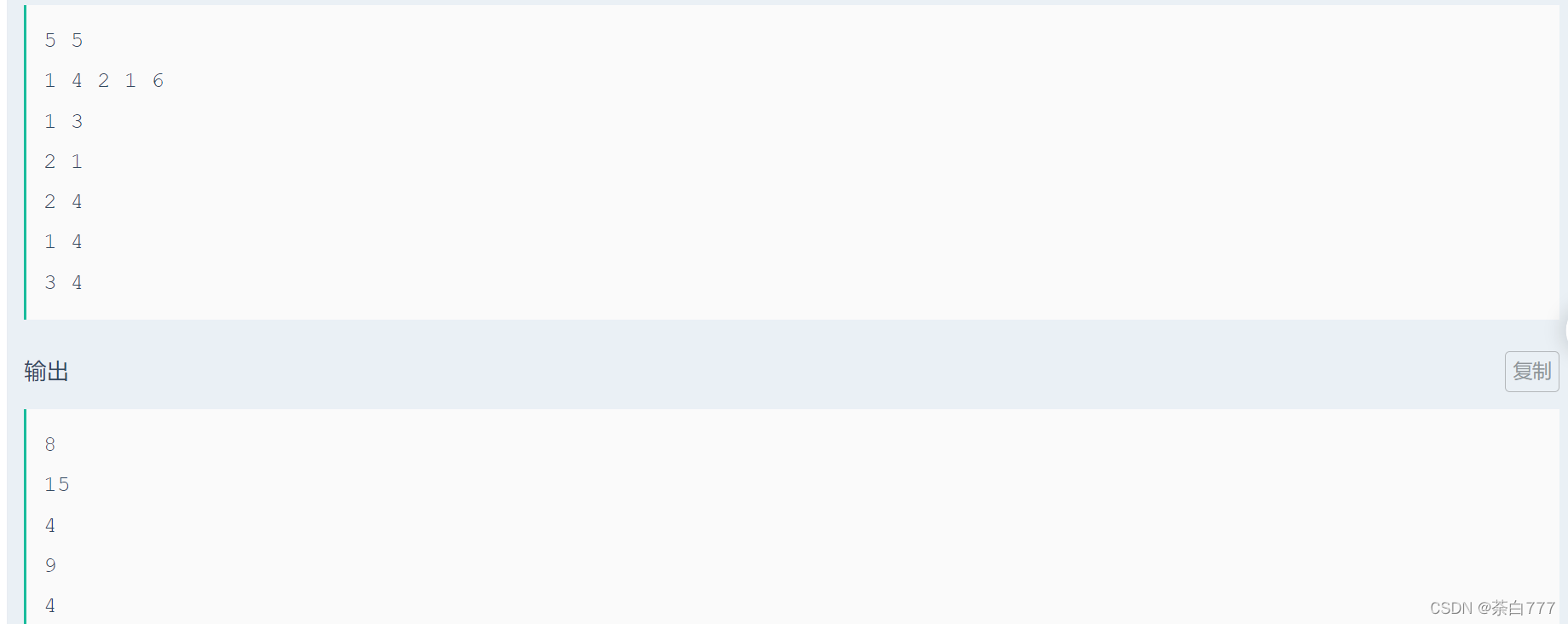
题意

每次询问一个区间$[L,R]$，问这个区间里的数最小不能拼凑的数是多少(最小是1)；

思路

先特判区间中的数包不包含$1$，不包含直接输出$1$；

假设包含$1$了，当前能够拼凑出的范围为$[1,sum]$；

如果我们想要不能取到的数变大，那么我们只能取$[1,sum+1]$中的数来拼凑；

比如说我们取$sum+2$来扩大，我们会发现$sum+1$这个点漏掉了，也就是根本没扩大；

至于更大的数就同理了；

举个例子，比如当前范围是$[1,5]$，我们如果得到了$2$；

那么范围就可以变成$[1,7]$，比如$6$可以通过全取加二然后去掉一，其他数同理；

---

现在的问题就要求我们支持一种操作；

• $[L,R]$中是否包含$[1,sum+1]$中的任何一个数

我们拿主席树转化一下

其实就是询问区间$[1,sum+1]$中的总和是多少；

如果$\sum [1,sum]\ne \sum [1,sum+1]$，那么就是存在上述的这样一个数了；

Code

#include <iostream>
#include <cstring>
#include <cstdio>
#include <algorithm>
#include <vector>using namespace std;typedef long long ll;const int N = 1e6 + 10;#define int llstruct Node{int lc,rc,sum;
}tr[N << 5];
int cnt,root[N];
int build(int l,int r){int q = ++cnt;tr[q].sum = 0;if(l == r){return q;}int mid = (l + r) >> 1;tr[q].lc = build(l,mid);tr[q].rc = build(mid+1,r);return q;
}int n,q,a[N];
vector<int> ve;
int get(int x){return lower_bound(ve.begin(),ve.end(),x)- ve.begin() + 1;
}
void push_up(int p){tr[p].sum = tr[tr[p].lc].sum+ tr[tr[p].rc].sum;
}
int update(int p,int l,int r,int x){int q = ++cnt;tr[q] = tr[p];if(l == r){tr[q].sum += ve[r-1];return q;}int mid = (l+r) >> 1;if(x <= mid) tr[q].lc = update(tr[p].lc,l,mid,x);else tr[q].rc = update(tr[p].rc,mid+1,r,x);push_up(q);return q;
}
ll query(int p,int q,int l,int r,ll tar){if(l == r) return tr[q].sum - tr[p].sum;int mid = (l + r) >> 1;if(tar <= mid) return query(tr[p].lc,tr[q].lc,l,mid,tar);else return tr[tr[q].lc].sum - tr[tr[p].lc].sum+ query(tr[p].rc,tr[q].rc,mid+1,r,tar);
}
int num[N];
void solve(){cin >> n >> q;for(int i=1;i<=n;++i){cin >> a[i];num[i] = num[i-1] + (a[i] == 1);ve.push_back(a[i]);}sort(ve.begin(),ve.end());ve.erase(unique(ve.begin(),ve.end()),ve.end());root[0] = build(1,n);for(int i=1;i<=n;++i){root[i] = update(root[i-1],1,n,get(a[i]));}ll ans = 0;int l,r,L,R;while(q--){cin >> l >> r;L = min((l+ans)%n+1,(r+ans)%n+1);R = max((l+ans)%n+1,(r+ans)%n+1);if(num[R] - num[L-1] == 0){ans = 1;cout << ans << '\n';continue;}ans = 1;while(1){int tar = upper_bound(ve.begin(),ve.end(),ans+1) - ve.begin();//映射到ans+1这个位置ll ret = query(root[L-1],root[R],1,n,tar);if(ret == ans){++ans;cout << ans << '\n';break;}else ans = ret;}}
}signed main(){std::ios::sync_with_stdio(false),cin.tie(0),cout.tie(0);solve();return 0;
}

L-Simone and graph coloring

题面

思路

假设序列为$[4,3,2,1]$；

那么肯定是个完全图，如下；

此时颜色必然为4种；

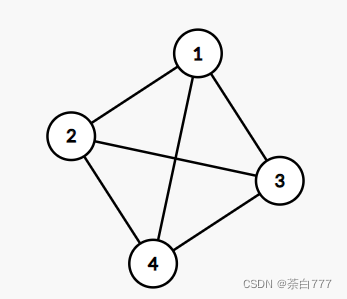
我们现在swap(1,2)，序列为$[4,3,1,2]$；

这样$<1,2>$之间是没有边的，如下；

不难想到，此时颜色为3种，我们可以让$1$和$2$上同一种颜色；

那么$1$既然不影响颜色种类数，我们自然可以把它抹掉；

考虑$[4,3,2]$，我们重复之前的步骤，swap(2,3)；

相信你已经发现，现在只需要2种颜色了；

---

那么无论多长的序列，最终都可以慢慢抹去；

那么我们就构造出了一种上色方案；

我们只需要求一个最长下降子序列即可，长度就是颜色种数；

上色就更简单了，$O(nlogn)$的LIS中，能够添加到末尾的，必然需要新的一种颜色；

而去替换别人的，那么相当于它们两是等价的，且满足被替换的数小于当前的数，即它们没有边；

那么我们直接取被替换的数的颜色即可；

Code

#include <iostream>
#include <cstring>
#include <cstdio>
#include <algorithm>using namespace std;typedef long long ll;const int N = 1e6 + 10;
int a[N],f[N],cnt;
int color[N];
void solve(){cnt = 0;int n;cin >> n;for(int i=1;i<=n;++i)cin >> a[i];for(int i=1;i<=n;++i){if(!cnt || f[cnt] > a[i]){f[++cnt] = a[i];color[i] = cnt;}else{//在[1,cnt]中找到第一个小于a[i]的替换int l = 1,r = cnt;while(l < r){int mid = (l+r) >> 1;if(f[mid] > a[i]) l = mid + 1;else r = mid;}f[r] = a[i];color[i] = r;}}cout << cnt << '\n';for(int i=1;i<=n;++i){cout << color[i] << ' ';}cout << '\n';
}signed main(){std::ios::sync_with_stdio(false),cin.tie(0),cout.tie(0);int t;cin >> t;while(t--)solve();return 0;
}

J-Parallel Sort

题面

思路

答案只有0，1，2三种情况；

考虑形成环的情况；

先考虑奇数环；

我们交换1-4，2-3；

发现此时就两两配对了；

再考虑偶数环；

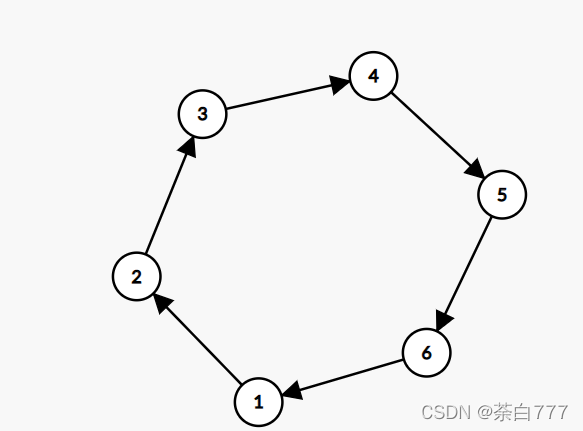
交换2-6，3-5后，两两配对了；

也就是说奇数环需要首先交换cnt/2次；
而偶数环需要首先交换cnt/2 - 1次，cnt为环上点的个数；

Code

#include <iostream>
#include <cstring>
#include <cstdio>
#include <algorithm>
#include <vector>
#include <utility>using namespace std;typedef long long ll;typedef pair<int,int> pii;const int N = 1e5 + 10;
int a[N],n,tot;
bool ck(){bool g = 1;for(int i=1;i<=n;++i){if(a[i] != i) g = 0;}return g;
}
vector<pii> swaps;
vector<int> loop[N];
bool vis[N];
void print_ve(){if(swaps.size() > 0){cout << swaps.size() << ' ';for(auto x : swaps){cout << x.first << ' ' << x.second << ' ';}cout << '\n';}
}
void solve_loop(int cnt,int arr[]){int sz = cnt / 2;if(cnt % 2 == 0) --sz;if(cnt & 1){for(int i=1;i<=sz;++i){int j = cnt - i + 1;int x = arr[i],y = arr[j];swap(a[x],a[y]);swaps.push_back({x,y});}}else{for(int i=1,u = 2,v = cnt;i<=sz;++i,++u,--v){int x = arr[u],y = arr[v];swap(a[x],a[y]);swaps.push_back({x,y});}}
}
void solve(){cin >> n;for(int i=1;i<=n;++i)cin >> a[i];	//0if(ck()){cout << 0 << '\n';return;}for(int i=1;i<=n;++i){if(a[i] == i) continue;int j = a[i];if(a[j] == i){swaps.push_back({i,j});swap(a[i],a[j]);}}//1if(ck()){cout << 1 << '\n';cout << swaps.size() << ' ';for(auto x : swaps)cout << x.first << ' ' << x.second << ' ';cout << '\n';return;}//2cout << 2 << '\n';//先处理出环for(int i=1;i<=n;++i){if(a[i] == i || vis[i]) continue;++tot;for(int j=i;!vis[j];j = a[j]){vis[j] = 1;loop[tot].push_back(j);}}int arr[N];for(int i=1;i<=tot;++i){int cnt = 0;for(auto x : loop[i]){arr[++cnt] = x;}solve_loop(cnt,arr);}print_ve();swaps.clear();for(int i=1;i<=n;++i){if(a[i] == i) continue;int j = a[i];if(a[j] == i){swaps.push_back({i,j});swap(a[i],a[j]);}}print_ve();}signed main(){std::ios::sync_with_stdio(false),cin.tie(0),cout.tie(0);solve();return 0;
}

C-Cities

题面

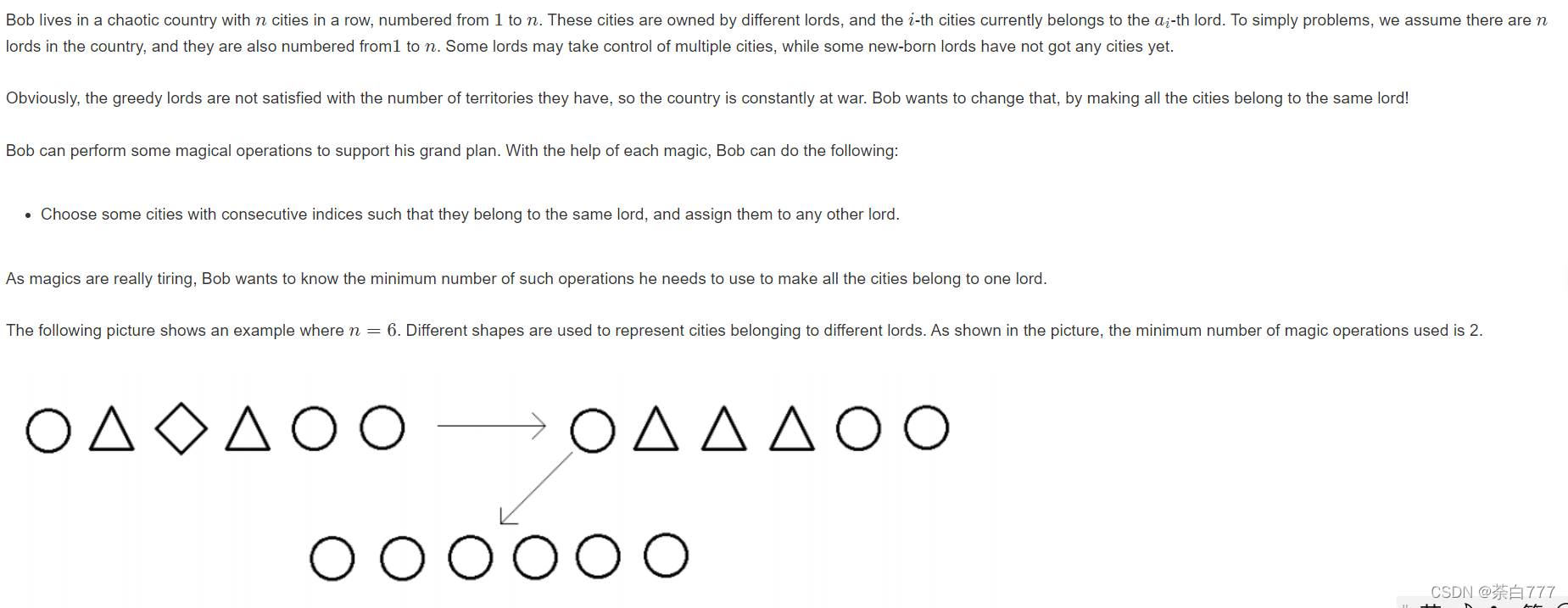
思路

$f(l,r)$表示将区间$(l,r)$染成$a(r)$的最小操作次；

不难想到，如果$l<k<r且a(k)=a(r)$，

那么$f(l,r)=f(l,k)+f(k+1,r)$

首先考虑暴力枚举，肯定会TLE的；

for(int len=2;len<=n;++len){for(int l=1;l+len-1<=n;++l){int r = l + len - 1;f[l][r] = min(f[l][r],f[l][r-1]+1);for(int k=l;k<r;++k){if(a[k] == a[r])f[l][r] = min(f[l][r],f[l][k]+f[k+1][r]);}}

因为题目说每个lord至多15个地盘；

因此考虑用类似链表的操作，我们将每个颜色构造成一条链；

然后按上面枚举即可；

Code

#include <iostream>
#include <cstring>
#include <cstdio>
#include <cstdlib>
#include <algorithm>using namespace std;typedef long long ll;const int N = 5e3 + 10;int f[N][N],a[N],n;
void debug(){for(int L=1;L<=n;++L){for(int R=L;R<=n;++R){printf("f[%d][%d]=%d\n",L,R,f[L][R]);}}
}
int front[N],last[N];//front(i)链式存储颜色相同的
void solve(){cin >> n;memset(f,0x3f,sizeof f);for(int i=1;i<=n;++i){cin >> a[i],f[i][i] = 0;front[i] = last[i] = 0;}for(int i=1;i<=n;++i){front[i] = last[a[i]];last[a[i]] = i;}int L = 1;for(int i=2;i<=n;++i){if(a[i] != a[i-1]){f[L][i-1] = 0;L = i;}}f[L][n] = 0;for(int len=2;len<=n;++len){for(int l=1;l+len-1<=n;++l){int r = l + len - 1;f[l][r] = min(f[l][r],f[l][r-1]+1);for(int k=front[r];k>=l;k=front[k]){f[l][r] = min(f[l][r],f[l][k] + f[k+1][r]);}}}cout << f[1][n] << '\n';//debug();
}signed main(){std::ios::sync_with_stdio(false),cin.tie(0),cout.tie(0);int t;cin >> t;while(t--)solve();return 0;
}