算法热门：回文链表(LeetCode 234)

Part I、回文结构

1、 生活中的回文

处处飞花飞处处；潺潺碧水碧潺潺。
处处红花红处处；重重绿树绿重重。

这两句对联儿您或许不熟悉，但是看起来、读起来都格外地有意思。为什么呢？因为无论是正着读，抑或是倒着读，都是一样的效果。不信？您在回去读读看。经典的回文还有一个近乎人人皆知的：上海自来水来自海上。
是不是很神奇？其实，回文不仅存在于文学，数学里也可以见到回文的影子，比如12321就是个回文数字。
生活中的回文还多的是，不过这并不是我们今天谈论的重点，且往下看。

2、解读“回文”

看了这么多例子，不难发现，回文结构最特殊的点在于它的前后对称性。这种前后对称性具体体现在：第一个对应倒数第一个，第二个对应倒数第二个，依次类推。

在编程中，我们接触的最早的应该就是回文字符串的判断——
给定一个字符串，让你判断它是否是回文结构。很简单，我们只需要头尾两个指针，然后判断它们指向的字符相不相等就可以了。

int left = 0, right = strlen(str);
while(left < right)
{if(str[left] != str[right])break;left++;right--;
}

是不是很easy？
而这一切的简单都来源于字符数组的随机存储性。我们可以很轻易地访问数组的任意一个成员，但是这放在链表中就行不通了，因为链表不支持随机读取，怎么办呢？

Part II、 回文链表

我们先来看看回文链表长啥样：

回文是指链表的数据具有前后对称性。但是可惜的是，对于这种单向链表，我们没办法从最后一个结点开始往前遍历。

第一想法

既然链表不能随机读取，那我就让它变得能随机读取不就好了？怎么做呢？把它的每一个数据单独拿出来存放在一个数组中，前后同时遍历，这样不就可以了吗？

bool isPalindrome(struct ListNode* head)
{struct ListNode* cur = head;//用来遍历链表int len = 0;//记录链表长度while(cur){len++;cur = cur->next;}//遍历链表，确定链表长度，便于开辟数组int* p = (int*)malloc(len*sizeof(int));int i = 0;cur = head;while(cur){p[i++] = cur->val;cur = cur->next;}int left = 0, right = len - 1;while(left < right){if(p[left] != p[right]){free(p);return false;}left++;right--;}free(p);return true;
}

我们放到LeetCode上跑一下代码后发现，速度还是很棒的，但是内存消耗上还是不尽人意。原因也很简单：为了存放链表的数据，我们需要额外开辟一个数组，这就带来了O(n)的空间复杂度。
有没有更好的方法呢？

思考+进阶

链表不能随机读取确实是个问题，有没有什么方法可以避开这个缺陷呢？
我们设想一个场景：如果我们有一张左右图案对称的纸，那么把它进行一个对折，它们是不是就能完美重合了？

我们把回文结构看成一张左右图案对称的纸，对它进行对折操作。而所谓的对折，其实就是以中间作为分界点，让回文结构的右边翻转一下，跟左边进行一 一 比较,那么显然，它们是完全相同的两个子结构。

如果放在链表中呢？我们就是以链表的中间节点为分界点，然后将链表的后半部分进行翻转，得到两个子链表——原链表的前一半和原链表后一半的翻转。然后将这两个子链表进行比较。
如果看过本系列前面的文章或者有刷题经验，这其中有两个关键字想必大家可能注意到了：1、中间结点
2、链表的翻转
由于篇幅关系，有关找中间节点的函数和翻转的函数我就不再赘述了，详细内容可以看一下下面两篇：链表的中间节点问题&反转单链表

详解

对于链表的中间节点，我们采取快慢指针的方法，如果有两个中间节点(偶数个结点的情况)，那么我们选择返回第二个中间节点。于是我们可以得到下面这幅图：

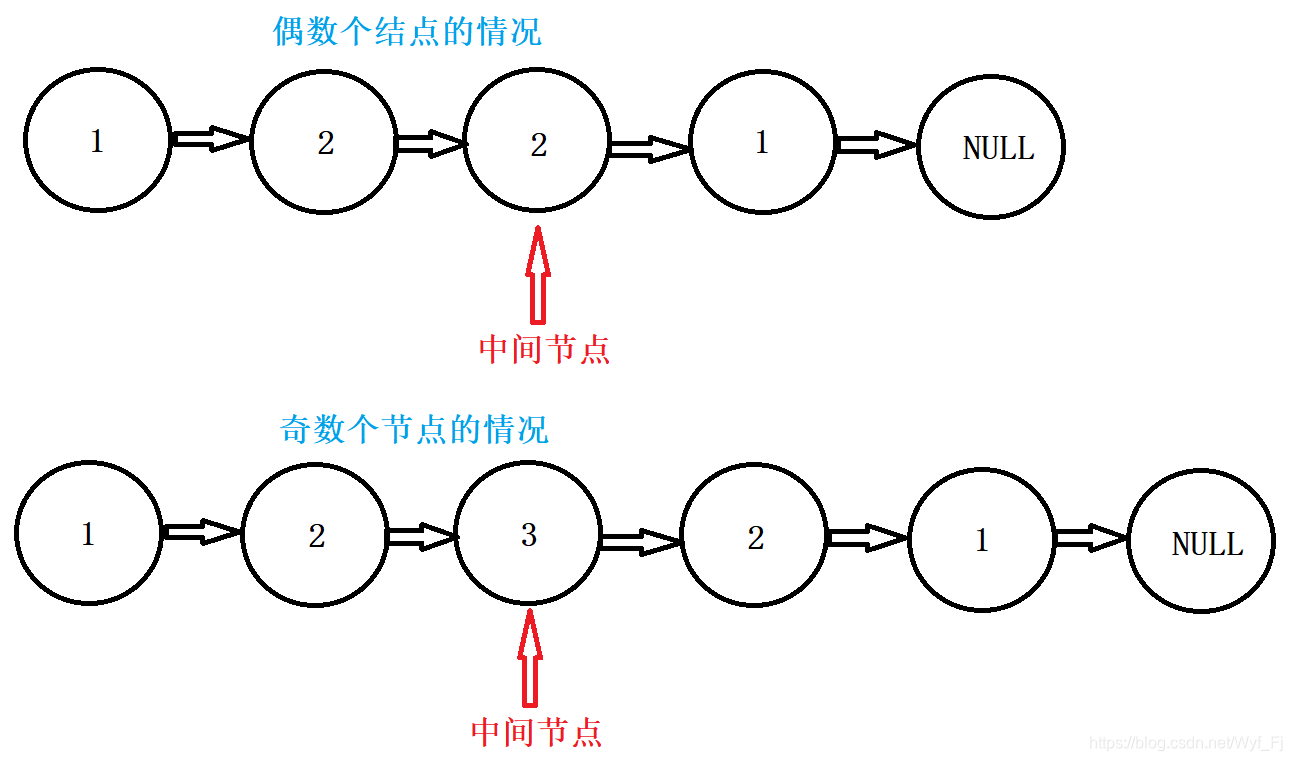
而找中间节点的操作也相对easy:

struct ListNode* fast = head, * slow = head;
while (fast && fast->next)
{slow = slow->next;fast = fast->next->next;
}//找到中间节点使链表分割

我愿将其称为：一步两步解法(一步两步似爪牙~)
中间节点的详解在这里！！！不明白的可以看看哦
然后，我们将从中间节点开始往后的这部分链表进行整体翻转，就会得到——


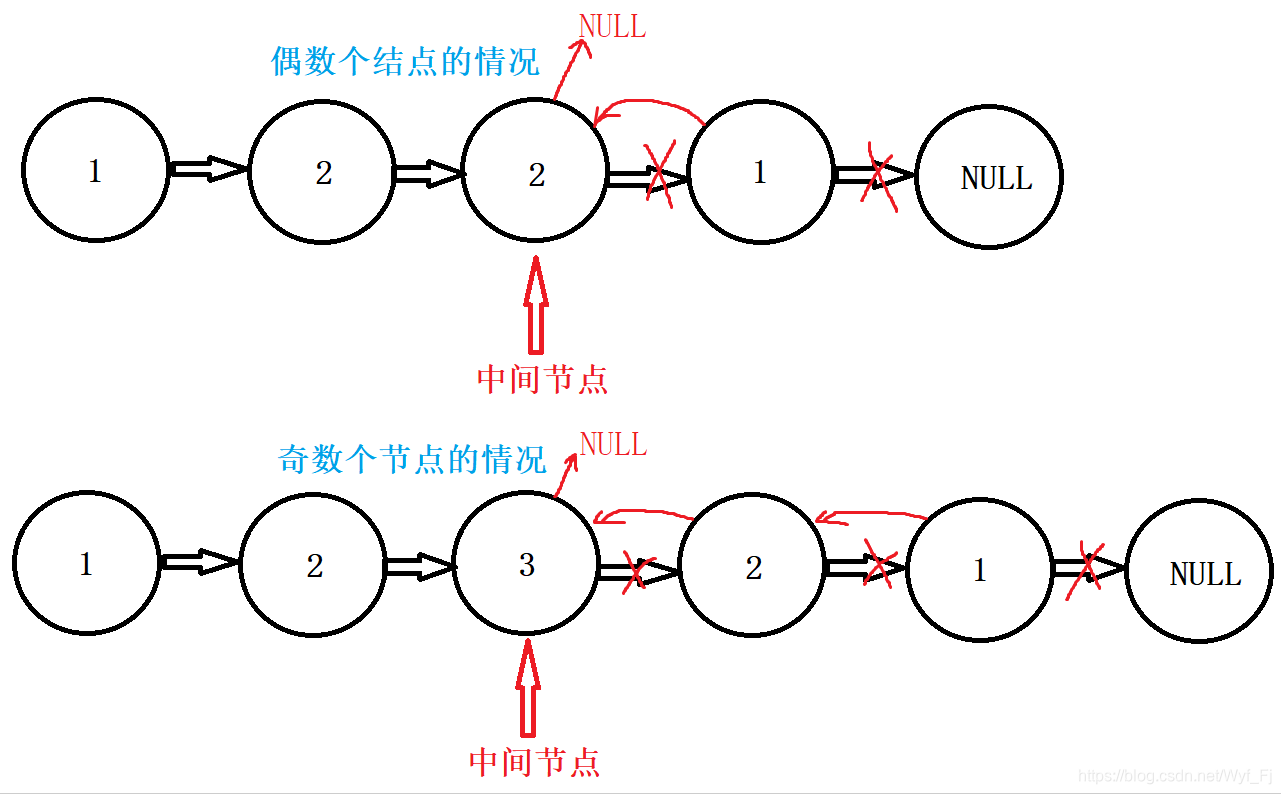
由于我们是将中间节点作为后半个子链表的头，进行翻转，于是原来的头变成了现在的尾。
翻转链表的代码：

struct ListNode* reverseList(struct ListNode* head)
{struct ListNode* cur = head, * newhead = NULL;while (cur){//头插到新链表struct ListNode* next = cur->next;cur->next = newhead;newhead = cur;cur = next;}return newhead;
}

翻转链表的详解在这里！！！戳一戳

然后我们要做的就是进行两个子链表的遍历和比较。

bool isPalindrome(struct ListNode* head)
{struct ListNode* fast = head, * slow = head;struct ListNode* p1 = head, * p2 = NULL;while (fast && fast->next){slow = slow->next;fast = fast->next->next;}//找到中间节点使链表分割p2 = reverseList(slow);//翻转后半个链表while(p2){if(p1->val != p2->val){return false;}p1 = p1->next;p2 = p2->next;}return true;
}

注意，这里遍历的控制条件要仔细分析一下：
对于偶数个结点的情况，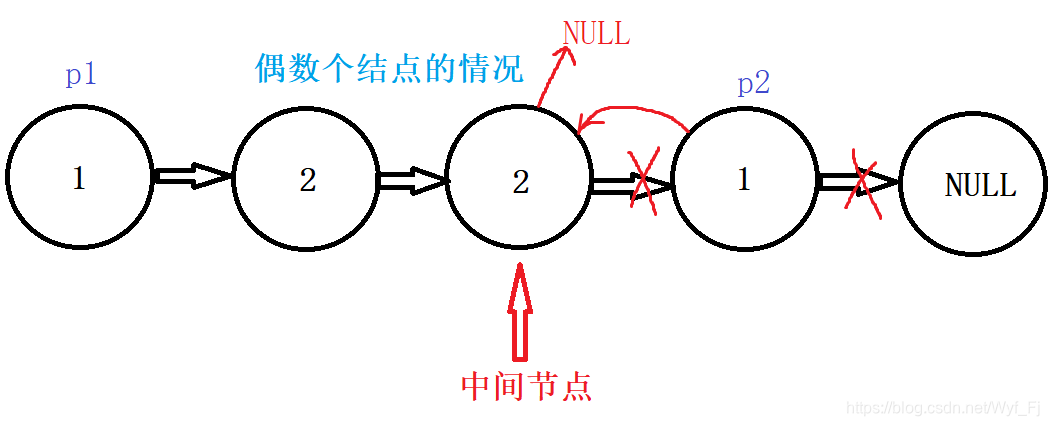
可以看到，前半个子链表是1->2->2->NULL，后半个翻转后的子链表是：1->2>NULL，很明显，这两个链表是不一样的，但我们我们可以选择再设置一个prev指针记录中间节点的前一个节点，然后让它的next指向NULL,此时p1链表就变成了1->2->NULL，不过也没必要。因为当我们的p2走到NULL时，p1也就走到了本应停下的位置：

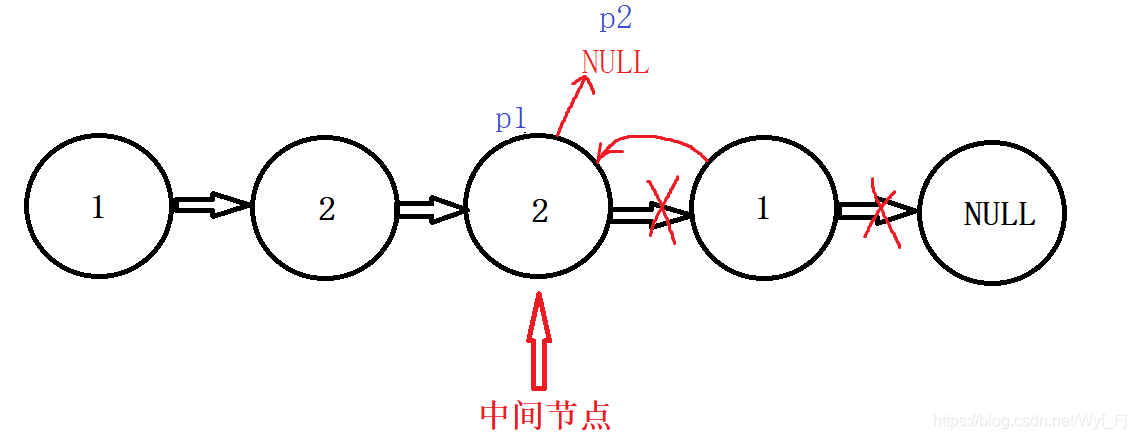
换句话说，p1、p2两个链表的节点数都应该是原链表的一半，但这个时候p1比p2多了一个结点。没关系，p2走到尾的时候p1也停下来就好咯。因此我们把p2!=NULL作为while的条件。
接下来看奇数个结点的情况：

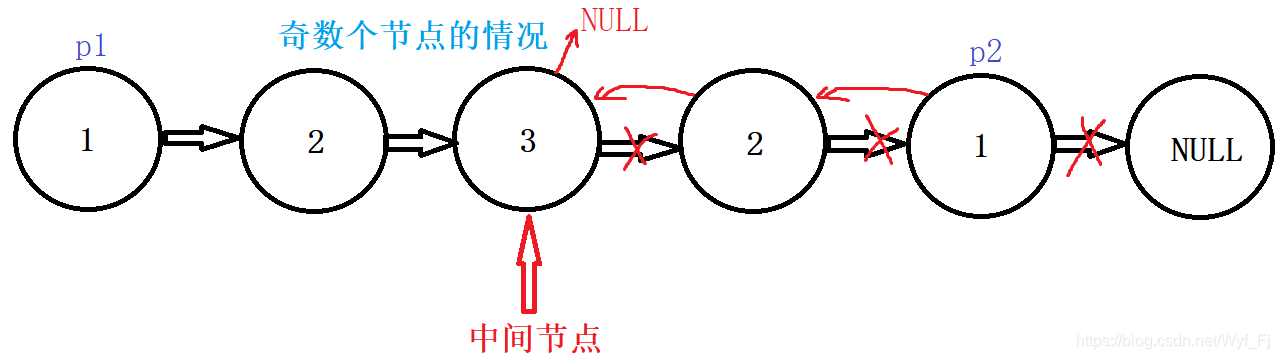
p1和p2都是1->2->3>NULL，那么遍历的条件可以是p1!=NULL，也可以是p2!=NULL。
所以，两种情况合并一下，就把p2!=NULL作为判断条件了！

Part III、总结也很重要

对于回文链表，我们用最朴实的想法实现了第一种解法，而受益于折纸思想，我们又完成了第二种找中间+翻转查重合的方法。
可能一开始我们想不到这些，但是随着时间的积累，很多优质的解法都会刻入你的DNA！

最后，我们先把代码汇总一下：

struct ListNode* reverseList(struct ListNode* head)
{struct ListNode* cur = head, * newhead = NULL;while (cur){//头插到新链表struct ListNode* next = cur->next;cur->next = newhead;newhead = cur;cur = next;}return newhead;
}
bool isPalindrome(struct ListNode* head)
{struct ListNode* fast = head, * slow = head;struct ListNode* p1 = head, * p2 = NULL;while (fast && fast->next){slow = slow->next;fast = fast->next->next;}//找到中间节点使链表分割p2 = reverseList(slow);while(p2){if(p1->val != p2->val){return false;}p1 = p1->next;p2 = p2->next;}return true;
}

欢迎关注博主，定期分享各种题解！让我们共同进步！