学习在外部Python脚本中运行Houdini的Python接口（hou模块）

0. 目标

学习在外部Python脚本（而非Houdini编辑器内部）使用 hou 。

主要参考Houdini官方文档 Command-Line Scripting 中的【Accessing hou from a Regular Python Shell】部分。我将要点记录在下：

1. 将Houdini的dll加入搜索路径

为了能使用 hou模块，Houdini的dll必须能链接到。
为此，可以将 “Houdini安装路径的bin文件夹” 加入环境变量Path中：

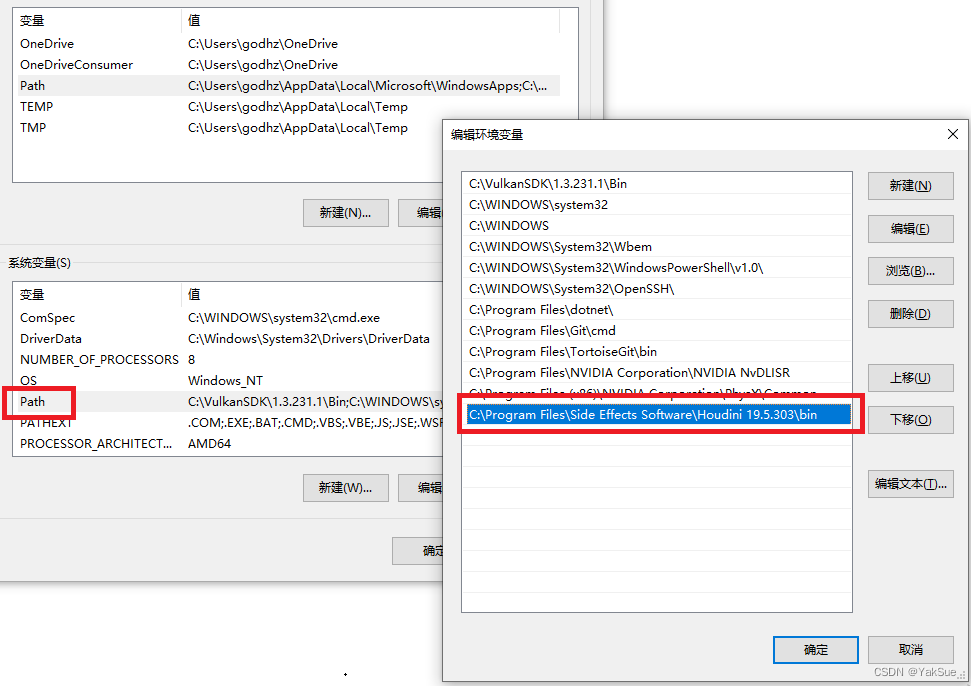
官方文档也有使用os.add_dll_directory在脚本中加入路径的方式。可惜我所使用的python版本还未支持（可通过 hasattr(os, “add_dll_directory”) 返回值来判断）。

2. 加入hou模块python文件的路径

根据所安装的Houdini版本和所用的Python版本，此路径在 $HFS/houdini/pythonX.Ylibs
比如，我这里就是：C:/Program Files/Side Effects Software/Houdini 19.5.303/houdini/python3.7libs

因此，在 import hou之前，需要使用sys.path.append将此路径加入。

在import hou时，Python会找到Houdini的库，并创建一个空白的Session。

3. 测试

测试脚本如下：

import sys
sys.path.append("C:/Program Files/Side Effects Software/Houdini 19.5.303/houdini/python3.7libs")
import hou#测试使用hou模块：
obj = hou.node("/obj")
obj.createNode("geo", "foo")
hou.hipFile.save("D:/Temp/MyTest0708.hip")

然后在命令行中运行，比如

C:/python-3.7.9-embed-amd64/python.exe D:/Temp/Test0708.py

这将保存一个 D:/Temp/MyTest0708.hip 文件。

总结

• Houdini的dll需要加入搜索路径，可以通过加入环境变量Path解决。
• import hou之前，需要确保模块的路径能被找到，否则使用sys.path.append加入。
• 在import hou时，Python会找到Houdini的库，并创建一个空白的Session。

其他问题记录

官方文档的测试脚本中，还有getdlopenflags相关的逻辑。
具体是，开始时：

    # Importing hou will load Houdini's libraries and initialize Houdini.# This will cause Houdini to load any HDK extensions written in C++.# These extensions need to link against Houdini's libraries,# so the symbols from Houdini's libraries must be visible to other# libraries that Houdini loads.  To make the symbols visible, we add the# RTLD_GLOBAL dlopen flag.if hasattr(sys, "setdlopenflags"):old_dlopen_flags = sys.getdlopenflags()sys.setdlopenflags(old_dlopen_flags | os.RTLD_GLOBAL)

结束时：

    # Reset dlopen flags back to their original value.if hasattr(sys, "setdlopenflags"):sys.setdlopenflags(old_dlopen_flags)

我这里没有做这个操作，不知道后续会不会有影响。