基于模糊 PID 的双容水箱液位控制系统设计

本文主要是介绍基于模糊 PID 的双容水箱液位控制系统设计，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

摘要

双容水箱液位控制系统是一个非线性的、延迟大的、易受扰动的系统，本文研究时，利用泰勒展开，将系统线性化，但是该系统受到扰动时，系统的数学模型发生略微改变。传统PID调节需要精确的数学模型，而模糊控制下的PID对数学模型的精确性不高，故而对于非线性的系统利用模糊控制下的PID往往会优于传统PID。本文将以双容水箱液位控制系统为背景，将数学模型参数多次变动，探讨模糊控制下的PID调节，分析其响应曲线。

本次实验基于simulink为仿真平台，搭建Fuzzy-PID实验环境，对模糊PID进行研究学习。

1.模型的建立

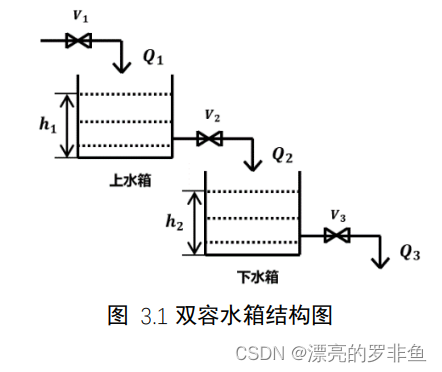
双容水箱系统结构图如图所示，上水箱进水阀𝑉1的开度控制上水箱流入量𝑄1，出水阀𝑉2流出量为𝑄2，上水箱的液位ℎ1由𝑄1和𝑄2来确定;下水箱进水阀𝑉2流入量为𝑄2，出水阀𝑉3 流出量为𝑄3，下水箱的液位ℎ2由进水量𝑄2和出水量𝑄3共同确定。在控制过程中 𝑉2、𝑉3保持不变，系统主要控制任务是通过调节𝑉1的开度来控制下水箱的液位ℎ2，使其测量值与设定值相等。下面介绍双容水箱建模过程。根据动态物料平衡关系列出下列方程：

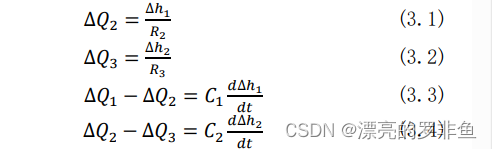
(3.1)式~(3.4)式中𝐶1和𝐶2分别为上水箱和下水箱的溶液系数，𝑅2和𝑅3分别为阀门𝑉2和𝑉3的液阻，将式(3.1)、(3.2)代入式(3.4)，可得

由此可得

对(3.6)求微分，得

将式(3.1)、(3.2)、(3.5)、(3.7)代入(3.3)并整理有

令𝑇1 = 𝐶1𝑅2为上容水箱的时间常数，𝑇2 = 𝐶2𝑅3为下容水箱的时间常数，𝐾 = 𝑅3对为系统对象的放大倍数，对上式进行拉氏变换可得传递函数：

若考虑延时环节，则

带入实验参数：

2.模糊PID控制系统介绍

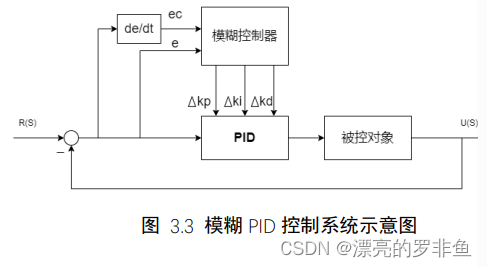
模糊控制理论是由美国著名的学者加利福尼亚大学教授𝑍𝑎𝑑𝑒ℎ · 𝐿 · 𝐴于1965年首先提出,它以模糊数学为基础,用语言规则表示方法和先进的计算机技术,由模糊推理进行决策的一种高级控制策略。模糊控制系统的核心组成是模糊控制器，一种数字控制系统，是反馈的闭环结构，它包括模糊数学知识，模糊逻辑推理和模糊规则，如图3.3。模糊𝑃𝐼𝐷控制根据误差𝑒和误差变化率𝑒𝑐,利用已经设定好的模糊控制规则调整𝑃𝐼𝐷参数，以达到提高控制系统动态性能的目的。

2.1模糊化

利用量化因子𝑘𝑒、𝑘𝑒𝑐将连续域内的误差𝑒和误差变化率𝑒𝑐离散化为模糊控制器的输入量 𝐸、𝐸𝑐，再根据隶属度函数（此处选择三角形隶属函数）求出其对应的模糊集合以便于进行模糊推理。

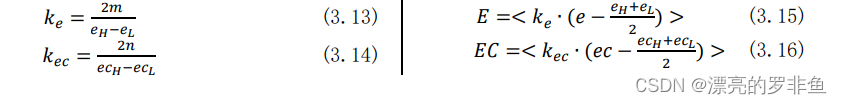
(3.13)和(3.14)式中𝑒𝐻、𝑒𝐿分别为实际中误差连续取值的最大值和最小值。𝑒𝑐𝐻、𝑒𝑐𝐿分别为实际中误差变化率连续取值的最大值和最小值。𝑚、𝑛为模糊控制器的输入量𝐸、𝐸𝑐的论域范围。本次实验𝑚 = 𝑛 = 3。

转化公式如(3.15)、(3.16)。转化后的𝐸、𝐸𝑐可作为隶属度函数的输入量，以求取𝑒、𝑒𝑐 对应的模糊集合。本次实验选择三角形隶属函数，如图3.2。

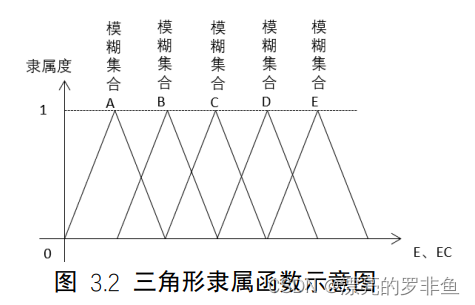
2.2模糊推理

根据已知的模糊关系和新的输入，确定推理输出𝐾𝑃、𝐾𝐼、𝐾𝐷的过程，本次设计利用的是前向推理。模糊𝑃𝐼𝐷推理规则如表 3.1。误差和误差变化率经过模糊化后可以获得𝐸、𝐸𝑐，再通过隶属度函数得到对应𝐸、𝐸𝑐的模糊集合。如表中给出规则，针对𝐸而言有NB\NM\NS\Z\PS\PM\PB7个模糊集合，而𝐸𝑐也有7个模糊集合。如果在某一时刻，𝐸为NB，𝐸𝑐为NS，那么此时对应的模糊PID的参数KP、KI、KD分别为PM、NM、NB。

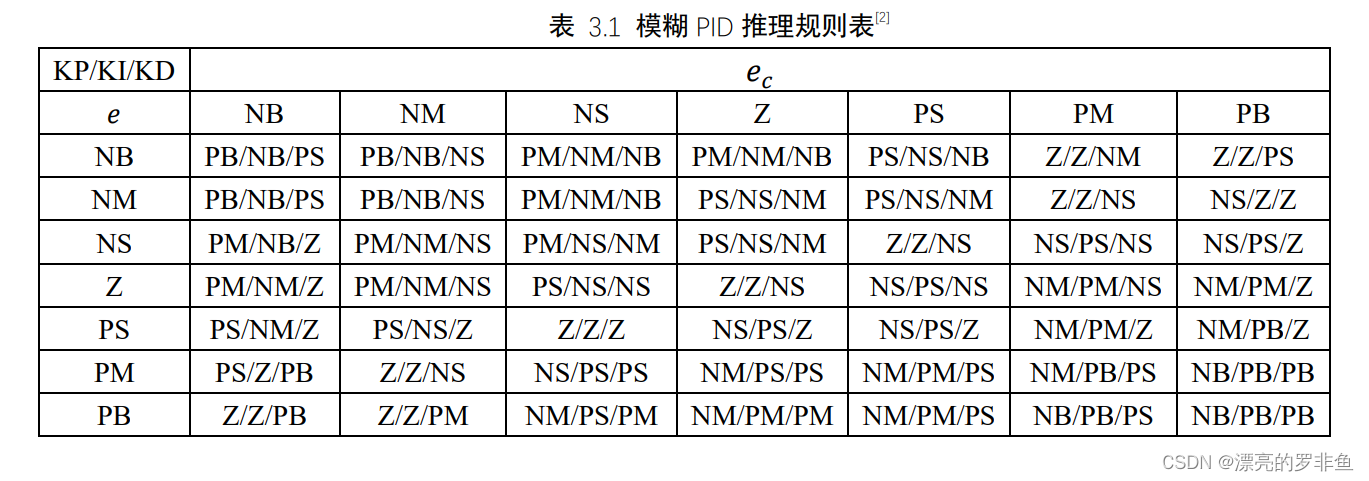
2.3去模糊化

将模糊推理的结论进一步转变为可用于驱动执行机构的定值定量信号即为去模糊化。利用比例因子𝑘𝑢(可用式(3.17)求得)和转化公式(3.18)求得实际作用于执行机构的输出𝑢。𝑈 是根据模糊推理机输出的模糊集合，通过最大隶属度法求得的最大隶属度的元素。

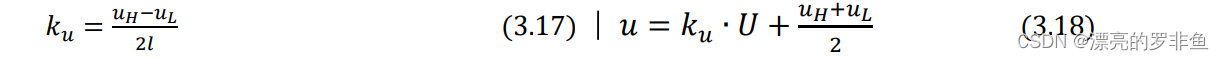
通过上述公式，可以得出KP、KI、KD对应的实际作用于执行机构的参数kp、ki、kd。

2.4 simulink仿真设置

打开matlab，创建一个.m文件，在命令行窗口输入”fuzzy“ ，弹出Fuzzy logic窗口，对模糊规则进行设置。

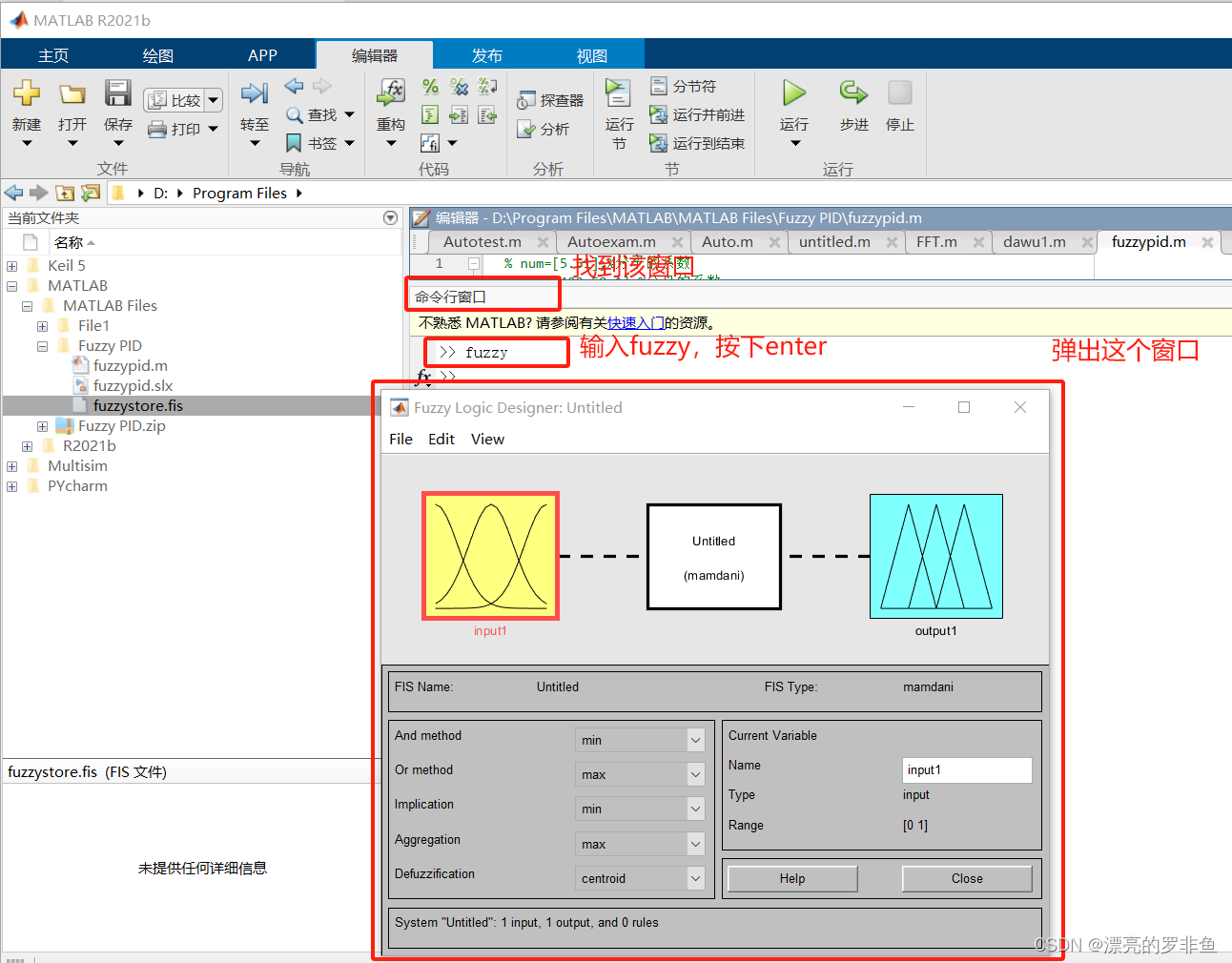
点击”Eidt“，更改输入输出变量的数量，改成2输入，3输出。

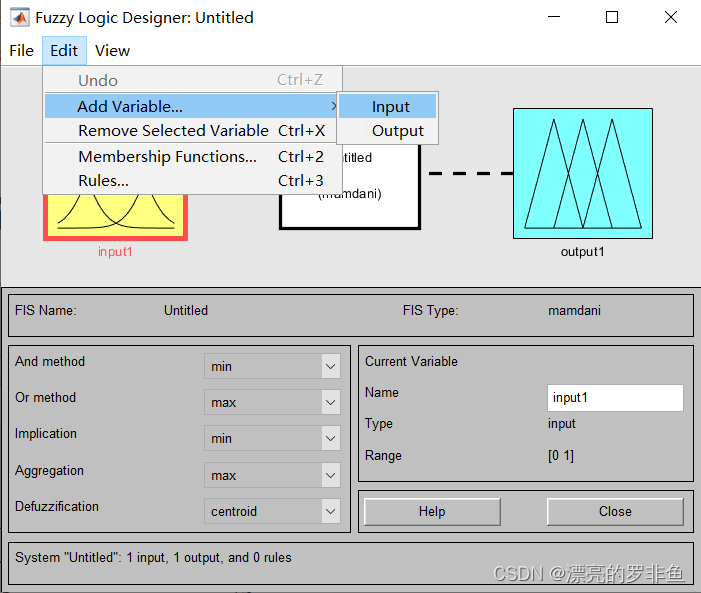
首先更改论域”Range“为[-6,6]，然后增加隶属度函数，选择"Edit"，然后选择”Add Custom MF...“，调整每个隶属度函数对应的论域范围，一共建立7个论域（模糊集合）。

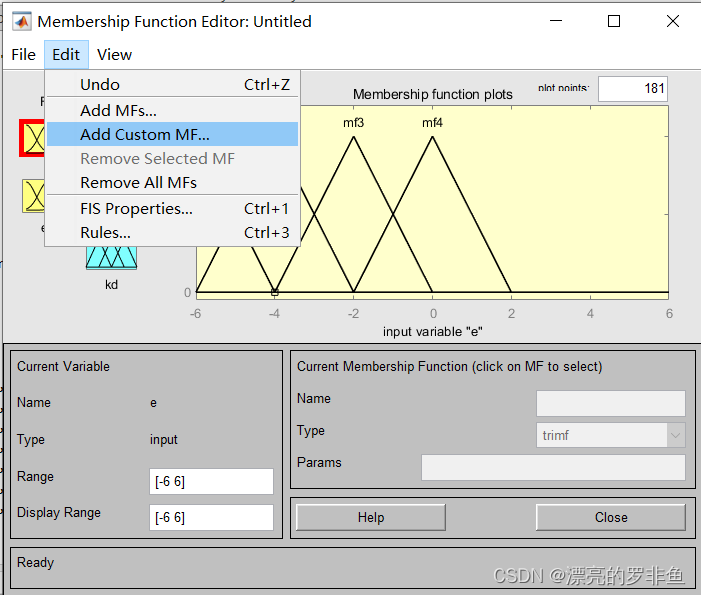
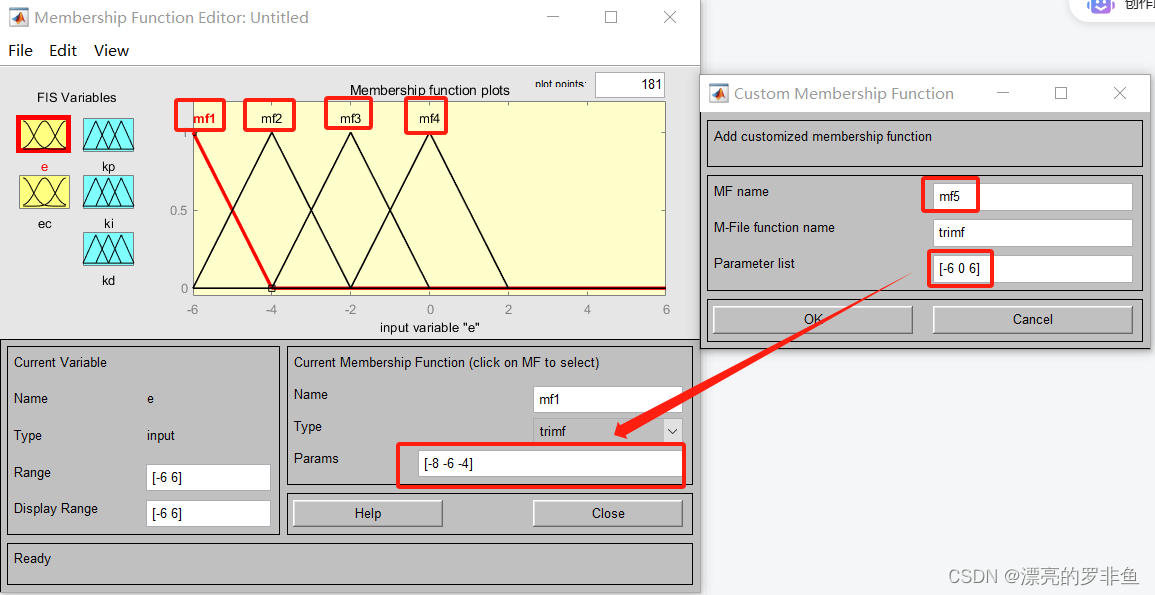
注意按照下面的数据对论域和隶属度函数进行设置，同理将两个输入和三个输出都按照如此格式设置，隶属度函数都选择三角函数"trimf"。可以对每个论域（模糊集合）进行改名，也就是将”mf1“按照模糊规则表的格式进行重命名。如下图的Input叫做“e”,每个隶属度函数分别叫做“NB”，“NM”，“NS”......

在模糊控制器的输入输出函数隶属度以及论域都设置好后，开始按照模糊规则表制定模糊rule。可以按照如下图进行设置。

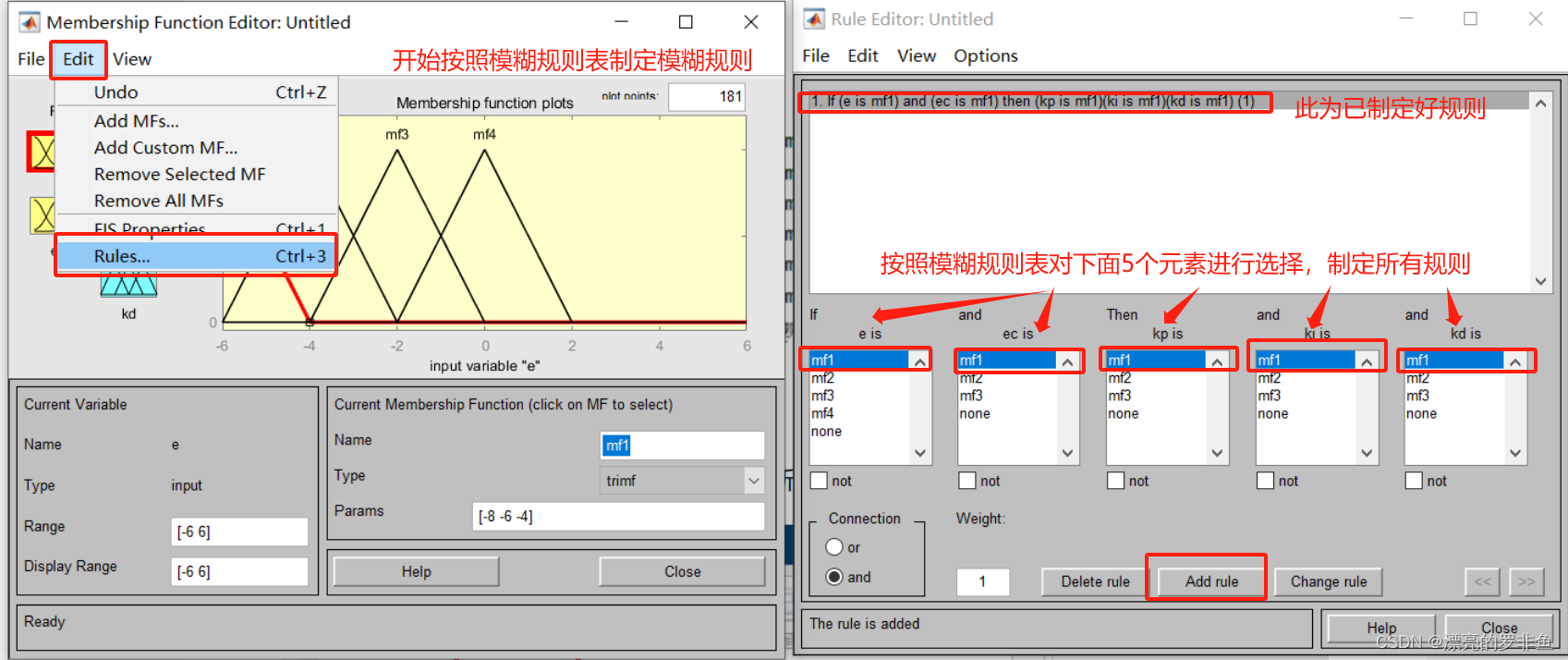
当所有规则都制定好后，则需保存该文件，该文件后缀为.fis。

打开simulink，新建工程后，按下图方式新建fuzzy模块。

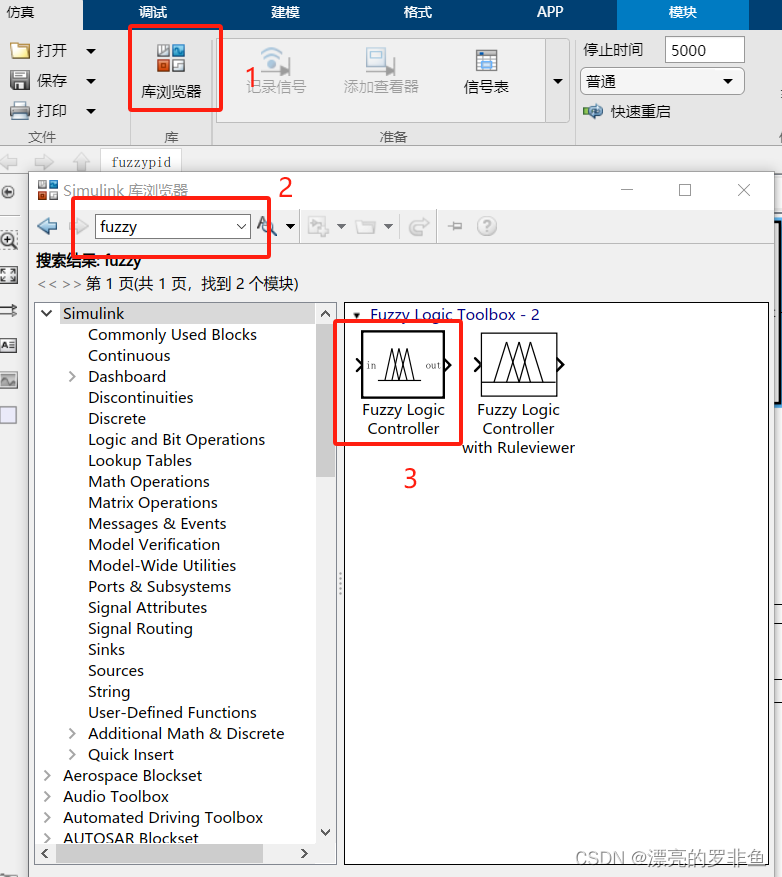
在该模块中导入之前建立好的.fis文件，双击该建立好的fuzzy模块即可。

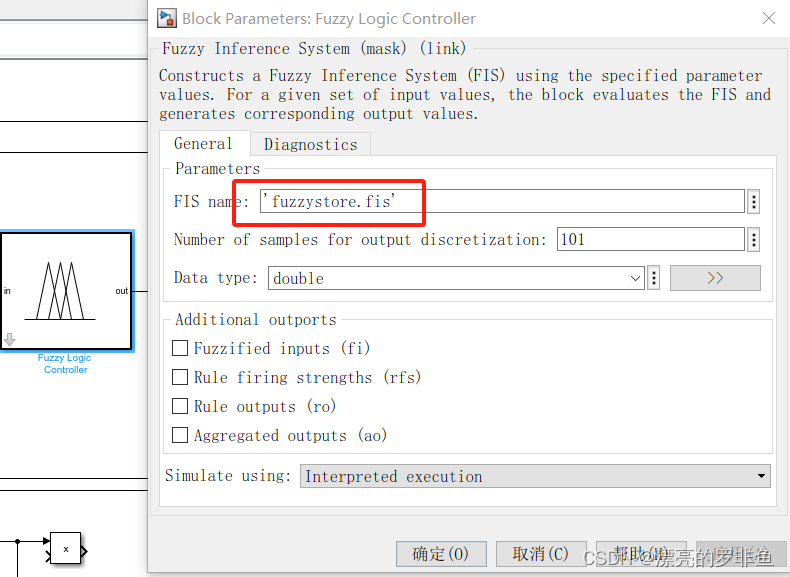
如此，仿真的模糊控制器即设计好了，然后按照图4.2在simulink中搭建电路图即可进行仿真调试。

3.临界比例法

此方法用于整定传统 PID 参数，以得到式(3.19)中，比较好的𝐾𝑃、𝑇𝐼、𝑇𝐷。

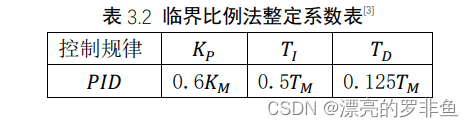
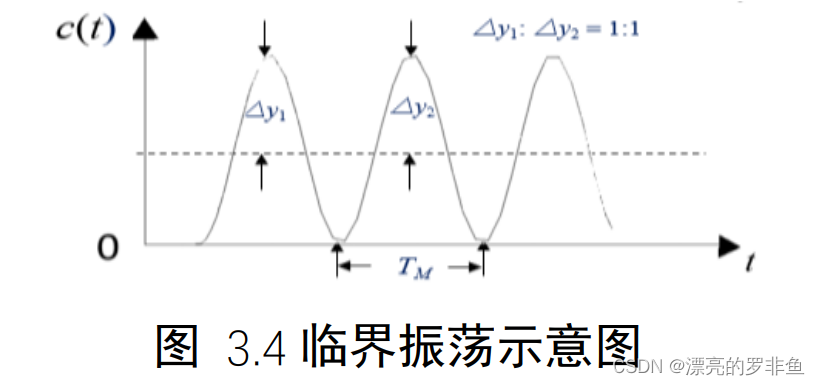
具体步骤为使𝑃𝐼𝐷处于纯比例作用(𝑇𝐼 = $\infty$ ,𝑇𝐷 = 0)，让系统处于闭环状态；然后从小到大改变𝐾𝑃，直到系统输出𝑐(𝑡)出现临界振荡，如图3.4；记下此时的临界振荡周期𝑇𝑀和比例系数𝐾𝑀；按如表 3.2 计算获得比例系数𝐾𝑃、积分系数𝑇𝐼和微分系数𝑇𝐷。

4.方案介绍

由图3.1可知，对象的被控制量为下水箱的液位ℎ2，控制量是流入上水箱中的流量𝑄1，手动阀𝑉2和𝑉3的开度都为定值，若以阶跃输入作为系统输入，则𝑉1的开度也是定值。用液位传感器测量下水箱的液位ℎ2，和设定的液位作差求出误差𝑒，并将误差求导得出误差变化率 𝑒𝑐。利用量化因子𝑘𝑒、𝑘𝑒𝑐进行模糊化，将误差𝑒、误差变化率𝑒𝑐离散化为模糊控制器的输入量𝐸、𝐸𝑐，再根据隶属度函数（此处选择三角形隶属函数）求出其对应的模糊集合，利用推理机，根据建立好的数据库和规则库(表3.1)进行模糊推理，得到模糊控制器的输出量𝐾𝑃、 𝐾𝐼、𝐾𝐷,再利用比例因子𝑘𝑢进行去模糊化，得到作用于𝑃𝐼𝐷三个矫正参数∆𝑘𝑝、∆𝑘𝑖、∆𝑘𝑑，将其与采用常规整定方法得到的 𝑘𝑝0、𝑘𝑖0、𝑘𝑑0预整定值进行相加处理，如式(3.20)~(3.22) 得到新的𝑃𝐼𝐷整定参数，用于系统的𝑃𝐼𝐷矫正。系统工作原理结构图如图3.5。

5.仿真结果讨论

本文的输入为单位阶跃输入，先搭建如图4.1的传统 PID 调节器，根据临界比例法得到式(3.12)所表示系统的𝐾𝑀 = 4.45、𝑇𝑀 = 703，所以推出𝐾𝑃 = 2.67、𝑇𝐼 = 351.5、𝑇𝐷 = 87.875，根据式(3.19)进而推出𝐾𝐼 = 0.0076、𝐾𝐷 = 234.63。经过微调后，得到𝐾𝑃 = 1.95、𝐾𝐼 = 0.001、 𝐾𝐷 = 255，此时的响应曲线的动态性能会有所改善。含有模糊控制器搭建的仿真电路图，如图4.2。对于模糊控制器的输入端，均接入饱和曲线限幅，且输入输出都配置了响应比例环节用于调节模糊参数。

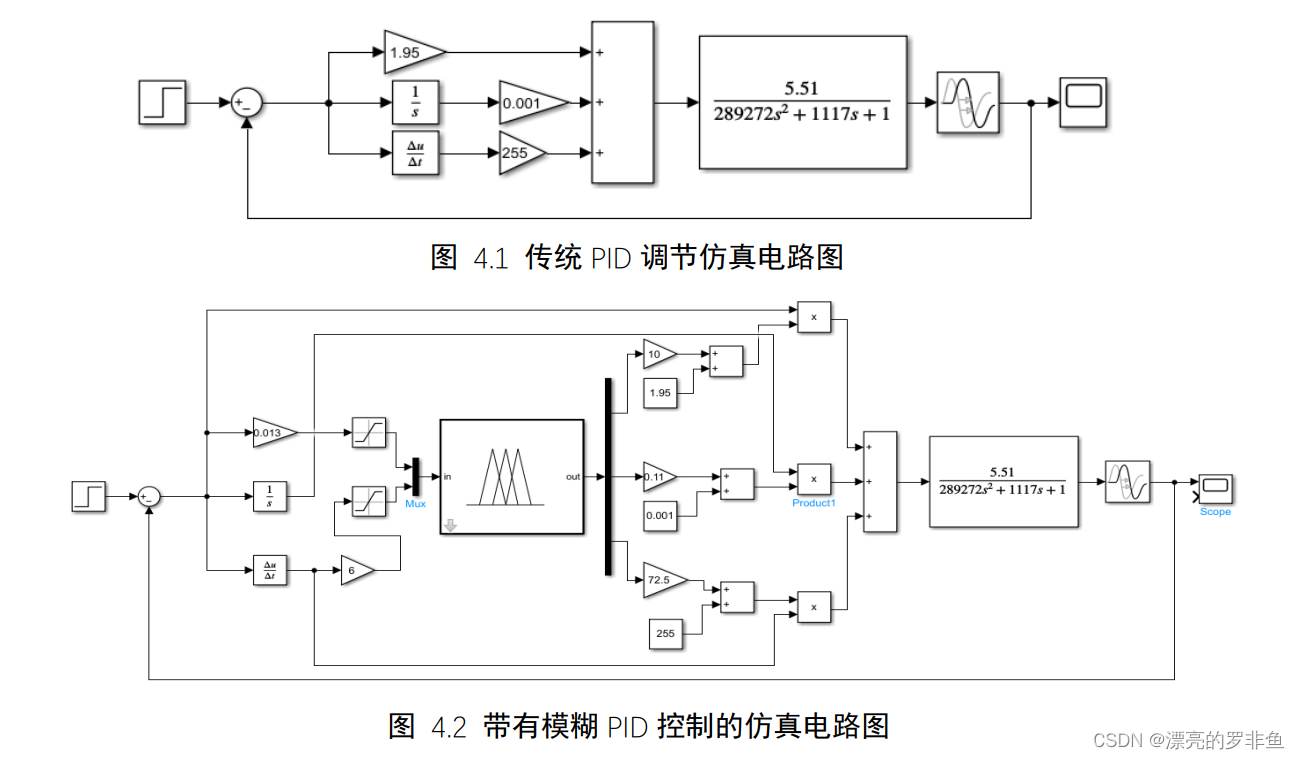
5.1传统 PID 控制与模糊 PID 控制的比较

仿真得到如图4.3输出曲线。

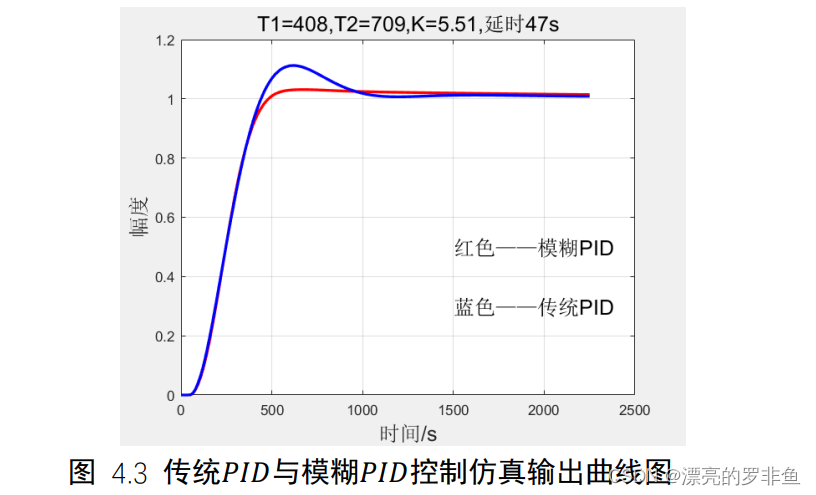
经过计算，传统𝑃𝐼𝐷的超调量为𝜎% = 11.3%，当误差带选取Δ = 0.05时，调节时间为𝑡𝑠 =865.637𝑠，稳态误差𝑒𝑠𝑠 = 0.002；对于模糊𝑃𝐼𝐷控制下的超调量为𝜎% = 3.2%，调节时间为 𝑡𝑠 = 425.427𝑠, 稳态误差𝑒𝑠𝑠 = 0.005。可以看到响应曲线的动态性能有明显提升,但是稳态性能稍有不足。但是当第一次超调后，传统𝑃𝐼𝐷的收敛速度明显大于模糊𝑃𝐼𝐷，出现这种现象的原因是模糊控制中信息的简单处理导致系统控制精度的降低，使得跟随能力有所下降。

5.2引入扰动后传统 PID 和模糊 PID 曲线变化

5.2.1引入阶跃扰动

在𝑡 = 1800𝑠时引入阶跃扰动，其幅值为0.2，观察响应曲线如图4.4。可以看到对于模糊 𝑃𝐼𝐷来说扰动对其影响要小于传统𝑃𝐼𝐷，但是其收敛速度依旧慢于传统𝑃𝐼𝐷。

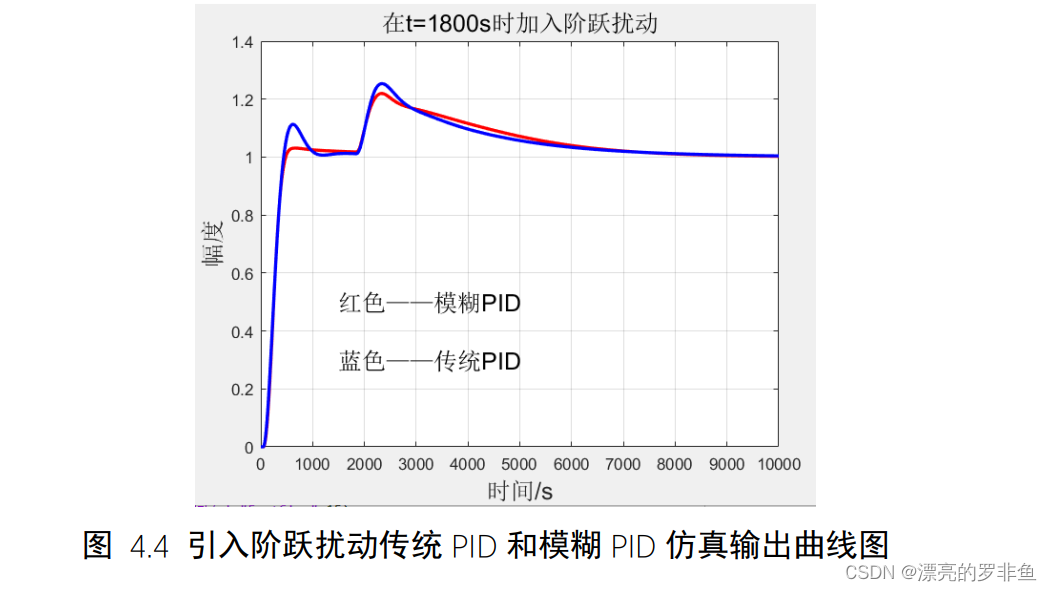
5.2.2扰动使模型改变

在这里考虑扰动使得𝑇1、𝑇2、𝐾和延迟时间发生变化导致的模型变化，具体响应曲线的动态性能指标如表4.1：可以看出当𝑇1、𝑇2、𝐾和延迟时间在一定范围内波动的时候，模糊𝑃𝐼𝐷的动态性能均优越于传统的𝑃𝐼𝐷。（𝑇1变化对应阀门𝑉2流阻𝑅2或者上水箱溶液系数𝐶1的变化; 𝑇2变化对应阀门𝑉3流阻𝑅3或者下水箱溶液系数𝐶2的变化；𝐾的变化对应阀门𝑉3流阻𝑅3的变化）。图4.5~图 4.7对应为模型变化但调节器不变的输出响应图，假定模型名称为模型𝐴、模型𝐵、模型𝐶。