本文主要是介绍运筹说 第81期 | 图与网络分析经典例题讲解,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!

通过前几期的学习,我们已经学会了图与网络分析的相关概念和基本方法的原理,并且掌握了图与网络分析相关模型的建立和具体的求解方法,本期小编带大家学习图与网络分析在经济管理中的应用。
在实际工作中,我们能发现图与网络分析在经济管理中有着许多应用,本期小编选择了其中一些典型例子,包括最小树问题、最短路问题、最大流问题和最小费用最大流问题,进行详细讲解。
01最小树问题
接下来我们先从经典的最小树问题开始讲起。
在现实生活中,最小生成树和最优二叉树有很高的实用价值。正确地理解掌握如何构造连通图的最小生成树问题以及最优二叉树问题,将会给我们带来巨大的经济效益和社会效益。随着最小生成树理论与算法的发展与完善,其在现实生活中的应用越来越广泛。本次小编选取了两道例题,包括经济学应用中具有代表性的最小投资问题以及数据通信问题,来为大家进行详细讲解。
例1、最小生成树问题
问题描述
发展轨道交通是解决城市内和城际间人员流动量大与交通设施运载力不足之间矛盾的主要途径,规划建设城际间快速轨道交通已经成为经济发展的迫切需要。某省份决定在包含9座城市的城市群内架设快速轨道交通干线,从最小投资角度出发,如何设计能连接城市群内所有城市的交通干线,并使得造价最低、总道路长度最短。
结合现实道路连通情况,对9座城市间交通道路图进行图论抽象,得到现实距离无向图如下图所示,不仅可以看到城市群所处的大致地理方位,亦可得知其间道路连通及其间距离的大致情况如下图所示。
问题解析
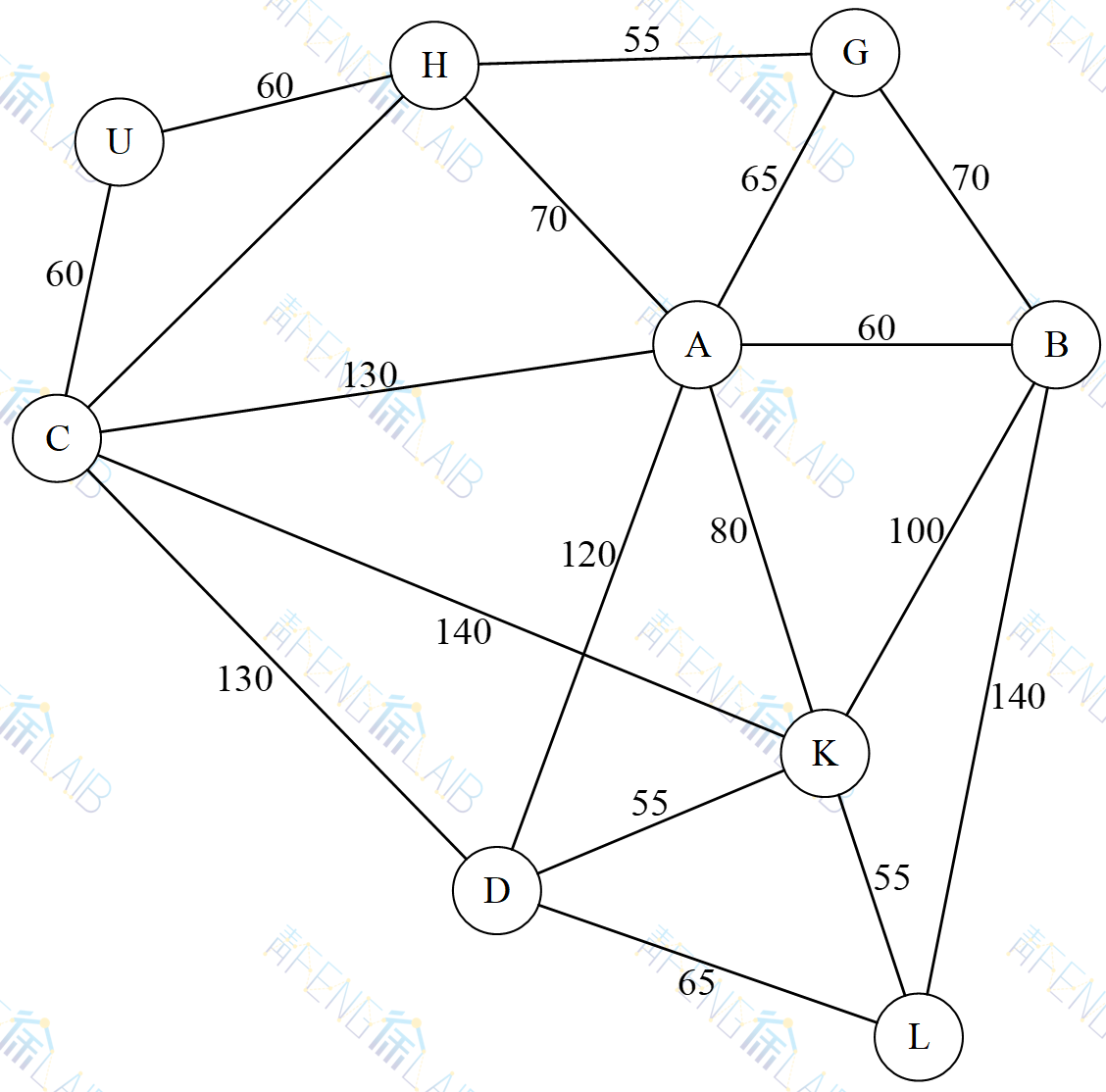
对于该城市群快速轨道交通干线问题,用小圆圈表示城市,用边表示城市之间联通道路,边上的权是用以表示两地间距离的公里数。网络的构成可采用点-点邻接关系来描述。边的权决定了路线选择的结果和最终轨道干线的投资。
利用第74期介绍的Kruskal算法对上图进行推算,最终可获得一条连通各城市、总路程最短(即投资最小)的交通干线,符合节约费用的原则。该算法的实质推论过程是:在无向图中,按照边的权值从小到大依次进行排序,从而获得边的权值递增序列,进而在图中依次递增序列选择边的集合。如果新选择的边与已经确认的边构成了回路(即首尾相连的环形边序列),则放弃该边,继续选择权递增的边序列中的下一条边,直到序列中的最后一条边。
问题求解
(1)首先选择权最小的边。从图中可知,DK,KL,GH的权均为55,从中任选一条均可。此处我们选择KL作为第一条边。

(2)接着再从除去边KL的其余边中选择权最小且不构成回路的第二条边。DK,GH权均为55,可从中任选一条。此处我们选择DK作为第二条边。

(3)选择HG作为第三条边。
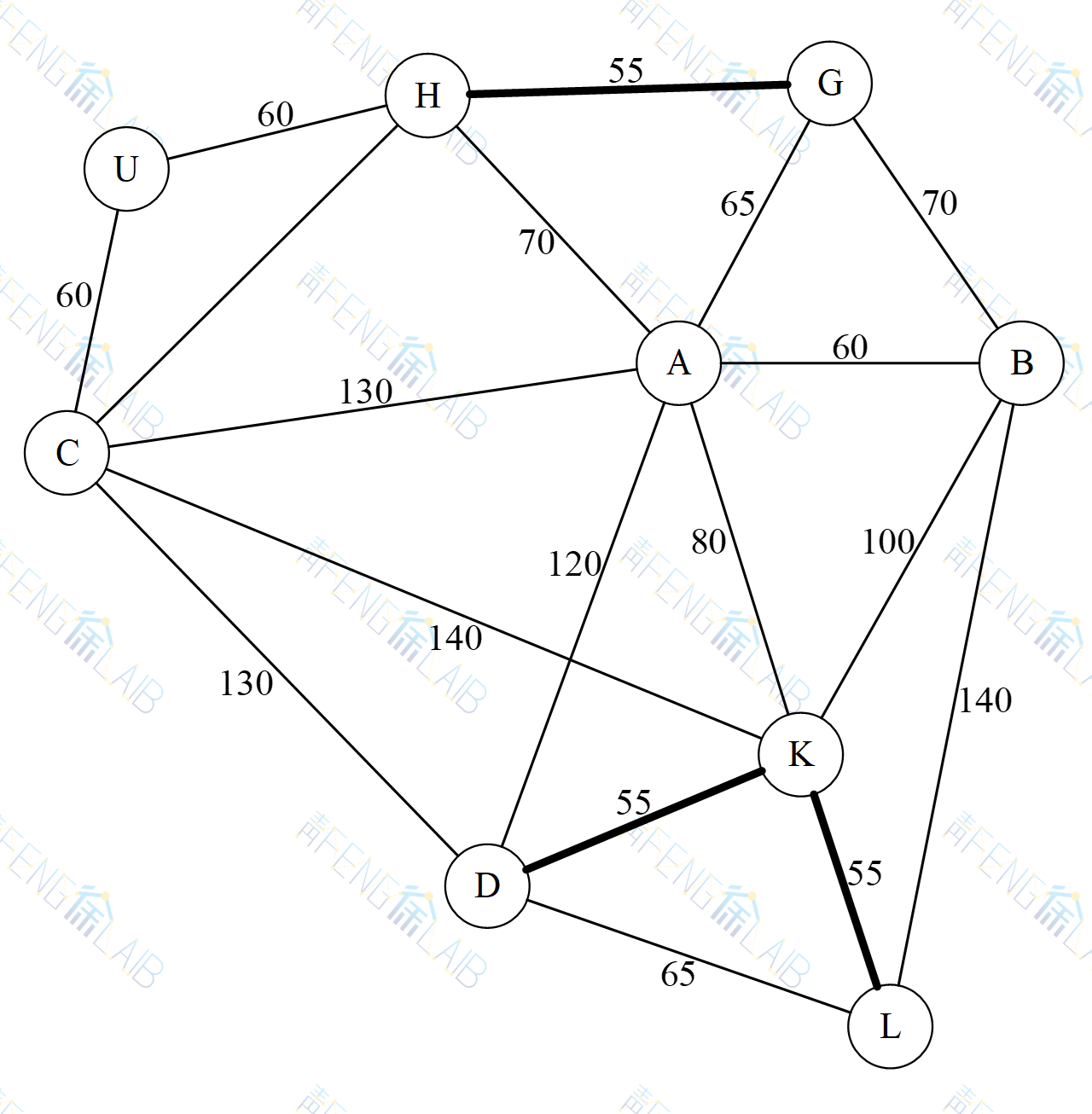
(4)除去KL,DK,GH三条边后,可以继续选择权为60的边CU,UH和AB,它们均可满足权最小且不构成回路的条件。

(5)DL,GA的权均为65,如果选择边DL,那么DK,KL和DL将构成封闭的三角形回路,故舍弃边DL,选择边GA。

(6)继续选择下一条边时也遇到构成回路的情况。边HA和GB的权为70,但如果选择它们必将产生回路,即:HG,GA,AH三角环回路或AG,AB,GB三角环回路。因此,不能选择此两边,必须选择不构成回路、但权稍大的其他边继续该算法。此处选择权为80的边AK。
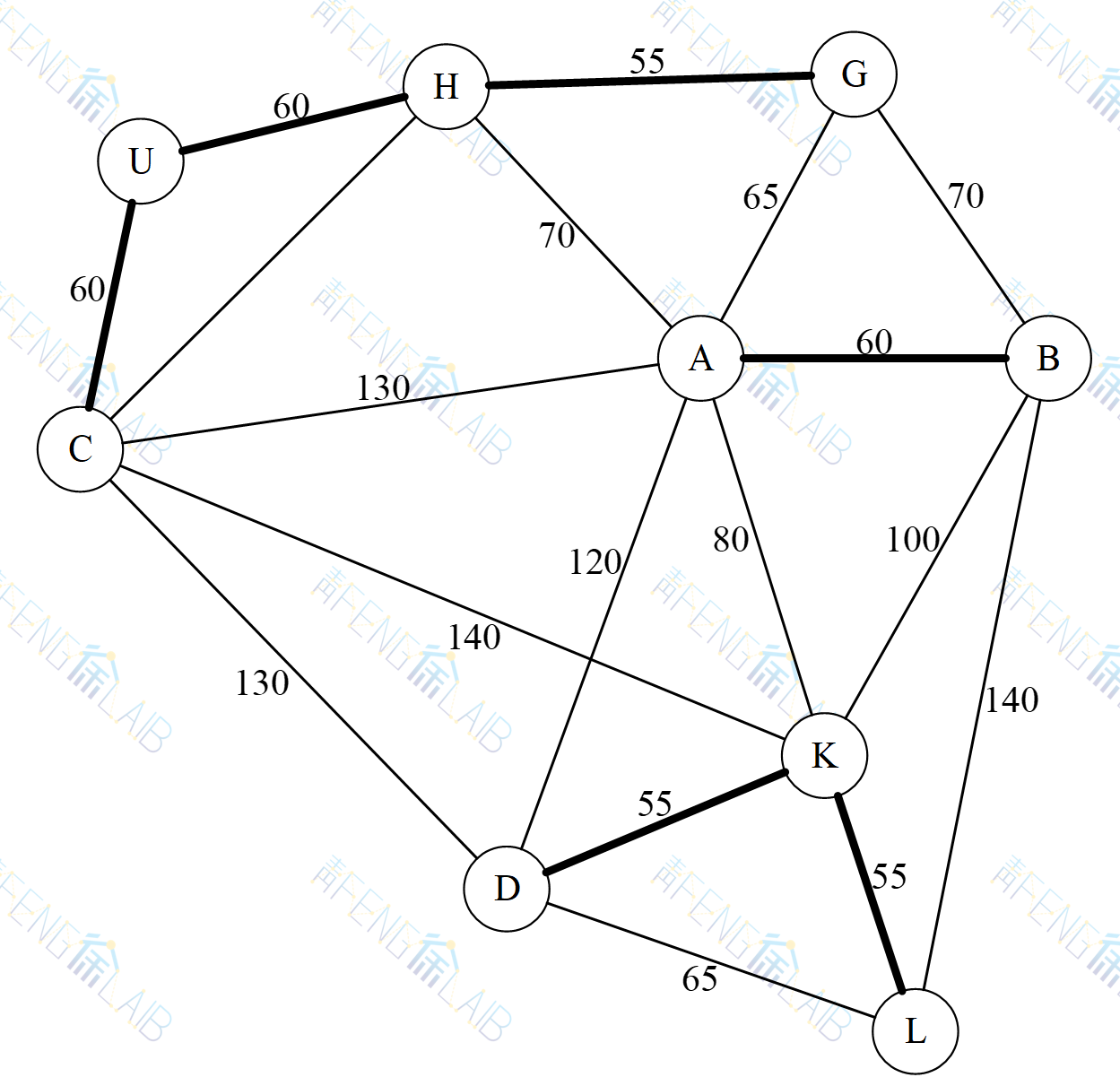
(7)此时继续算法将会全部产生回路,算法结束,图中粗线展示了根据算法求解最小生成树的过程。

得到最小生成树如下图所示:

例2、最优二叉树问题
下面小编带大家学习一下最优二叉树问题。先来看如下定义。
(1)节点的带权路径长度:从树根节点到某节点之间的路径长度与该节点上权值的乘积称为该节点的带权路径长度。
(2)树的带权路径长度(WPL):树中所有叶子节点的带权路径长度之和称为该树的带权路径长度。
最优二叉树又称霍夫曼树,它是n个带权叶子结点构成的所有二叉树中,带权路径长度WPL最小的二叉树。假设有n个权值,则构造出的霍夫曼树有n个叶子结点。n个权值分别设为w1,w2,…,wn,则霍夫曼树的构造规则为:
(1)将w1,w2,…,wn看成是有n棵树的森林(每棵树仅有一个结点);
(2)在森林中选出两个根结点的权值最小的树合并,作为一棵新树的左、右子树,且新树的根结点权值为其左、右子树根结点权值之和;
(3)从森林中删除选取的两棵树,并将新树加入森林;
(4)重复上面两步,直到森林中只剩一棵树为止,该树即为所求得的最优二叉树。
因此,霍夫曼树的特征有:
(1)越靠近根节点,权值越大;
(2)初始结点全是后来的叶子结点;
(3)叶子结点权值越大,离根节点越近(路径越短);
(4)如果把路径标上0和1,则每一个叶子结点有一个唯一编码(不定长)。
霍夫曼树的应用:霍夫曼编码
编码:在数据通信中,经常需要将传送的文字转换为二进制字符0、1组成的字符串,这个过程称为编码。
霍夫曼编码:设需要编码的字符集合为{d1,d2,...,dn},各个字符在电文中出现的次数集合为{w1,w2,...,wn},那么以d1,d2,...,dn作为叶子节点,以w1,w2,...,wn作为个节点的权值构造一颗霍夫曼树,一般规定霍夫曼树中左分支为0,右分支为1,则从根节点到叶节点所经过的分支对应的0和1序列就称为该节点对应字符的编码,这样的编码就是霍夫曼编码。
霍夫曼编码的优点在于能最大程度的节省空间。
问题描述
一组字符{A,B,C,D,E,F,G}出现的频率分别是{9,11,5,7,8,2,3},设计最经济的编码方案并求出带权路径长度。
问题求解
利用构造规则画出霍夫曼树:(不唯一,只要根结点是45就是对的)

将霍夫曼树所有的左子树标记为0,右子树标记为1(也可以左子树标1,右子树标0,霍夫曼编码和霍夫曼树不是唯一的,只要遵循一个统一的规定,就可以构建出霍夫曼编码),然后将所有的权值与字母对应起来。
相应的编码就是从根结点到相应位置的路径。

A对应的霍夫曼编码为00
B对应的霍夫曼编码为10
C对应的霍夫曼编码为010
D对应的霍夫曼编码为110
E对应的霍夫曼编码为111
F对应的霍夫曼编码为0110
G对应的霍夫曼编码为0111
WPL=9×2+11×2+5×3+7×3+8×3+2×4+3×4=120
即带权路径长度为120。
02最短路问题
最短路问题是在图的基础上衍生出来的,也是网络优化中的一个基本问题,广泛应用于计算机科学、交通工程、通信工程、系统工程、运筹学、信息论、控制理论等众多领域。本次小编选取一道公路网络运输中的最短路问题,运用第76期详细介绍的经典Dijkstra算法进行求解。
例3、最短路问题
问题描述
设6座v1,v2,...,v6城市之间的一个公路网如下图所示,每条公路为图中的边,边上的权数表示该段公路的长度(单位:百公里),假如小明处在城市v1,需要将某物品运送到所有的城市,那么从v1到v6应选择哪一路径可以使小明的费用最省。
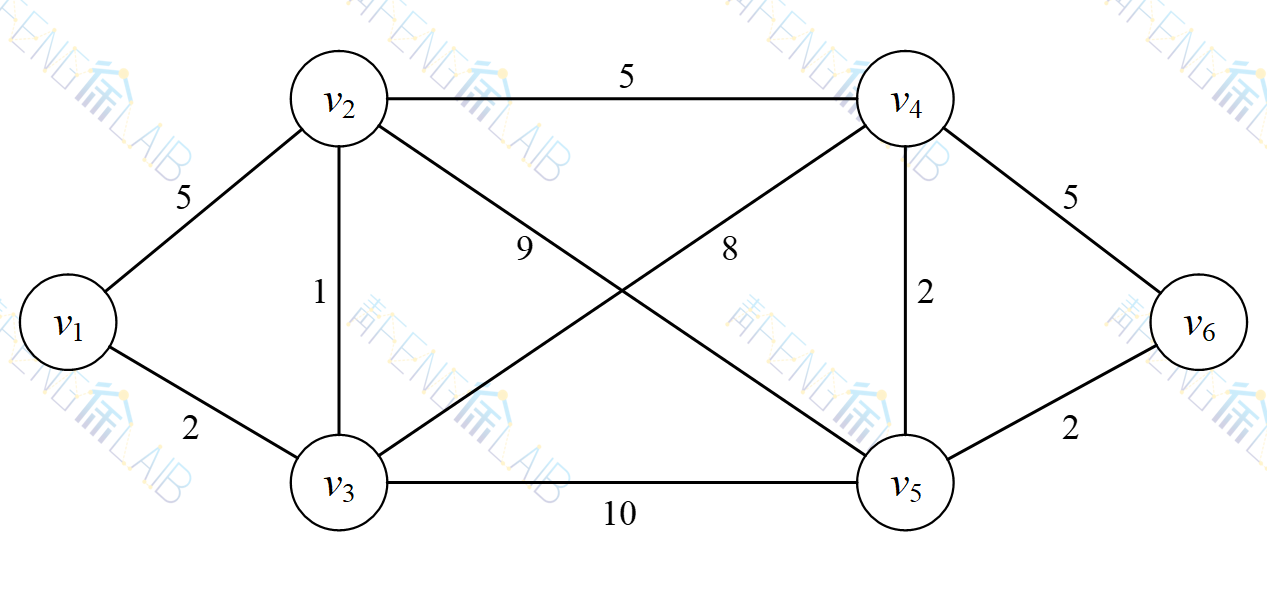
问题求解
解法一:Dijkstra算法
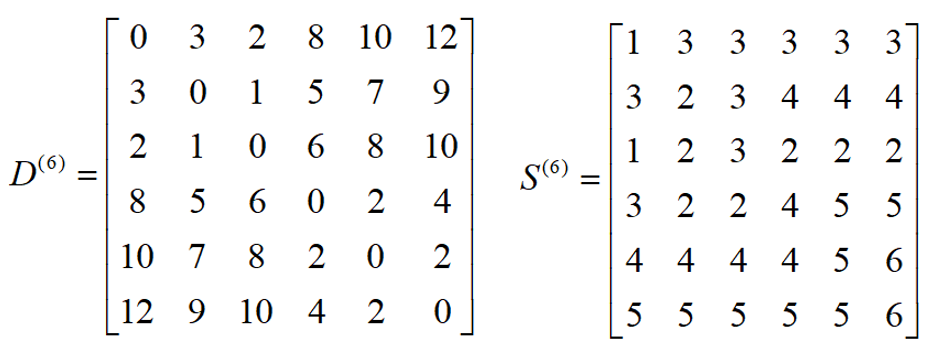
首先设每百公里所用费用一样,求v1到v6的费用最少,即求v1到v6的最短路线。为了方便计算,我们先作出该网络的距离矩阵,如下:

(1)设W(v1)=0,T(v)=∞,vj∈{v2,v3,v4,v5,v6};
(2)第一次迭代:
①计算T(vj),j=2,3,4,5,6如下:

②取minvj∈s-{T(vj)}=2=T(v3),令W(v3)=T(v3)=2
③由于k=3≠(n=6),令s-={v2,v4,v5,v6},i=3
第二次迭代:
①计算T(vj),j=2,4,5,6如下:

②取minvj∈s-{T(vj)}=3=T(v2),令W(v2)=T(v2)=3
③由于k=2≠(n=6),令s-={v4,v5,v6},i=2
第三次迭代:
①计算T(vj),j=4,5,6如下:

②取minvj∈s-{T(vj)}=8=T(v4),令W(v4)=T(v4)=8
③由于k=4≠(n=6),令s-={v5,v6},i=4
第四次迭代:
①计算T(vj),j=5,6如下:
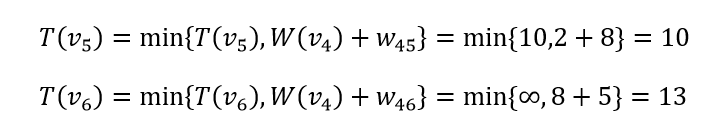
②取minvj∈s-{T(vj)}=10=T(v5),令W(v5)=T(v5)=10
③由于k=5≠(n=6),令s-={v6}
第五次迭代:
①计算T(vj),j=6如下:

③由于k=6=n,因此已经找到v1到v6的最短距离为12,计算结束。
(3)找最短路线,逆向追踪得:
v1→v3→v2→v4→v5→v6
最短距离为2+1+5+2+2=12,即按上述路线从城市v1到v6的距离最短,费用最省。
解法二:Floyd算法
某些问题中,要求网络上任意两点间的最短路。这类问题可以用Dijkstra算法依次改变起点的办法计算,但比较烦琐。这里介绍的Floyd方法来求解本例题,可直接求出网络中任意两点间的最短路,步骤如下:


回到例题本身,由上图可得:








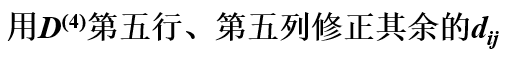

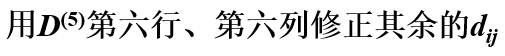
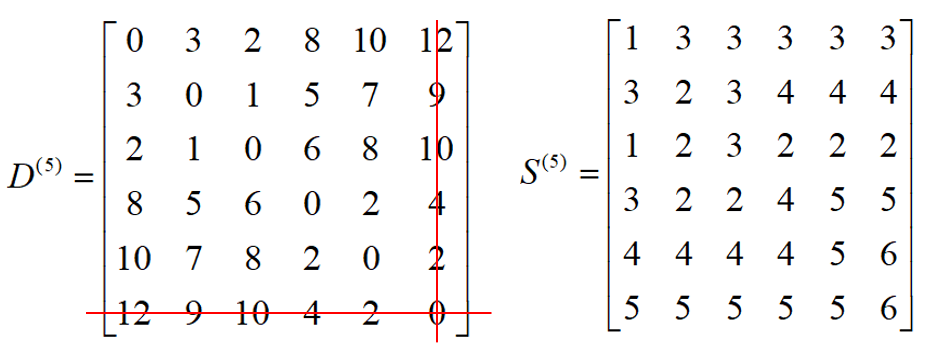

03最大流问题
最大流问题是一类应用极为广泛的问题,例如在交通运输网络中有人流、车流、货物流,供水网络中有水流,金融系统中有现金流,通信系统中有信息流等等。20世纪70年代福特(Ford)、富克逊(Fulkerson)建立的“网络流理论”,是网络应用的重要组成部分。本次小编选取一道电力公司供电问题中的最大流问题,运用第78期详细介绍的Ford-Fulkerson 标号算法进行求解。
例4、最大流问题
问题描述
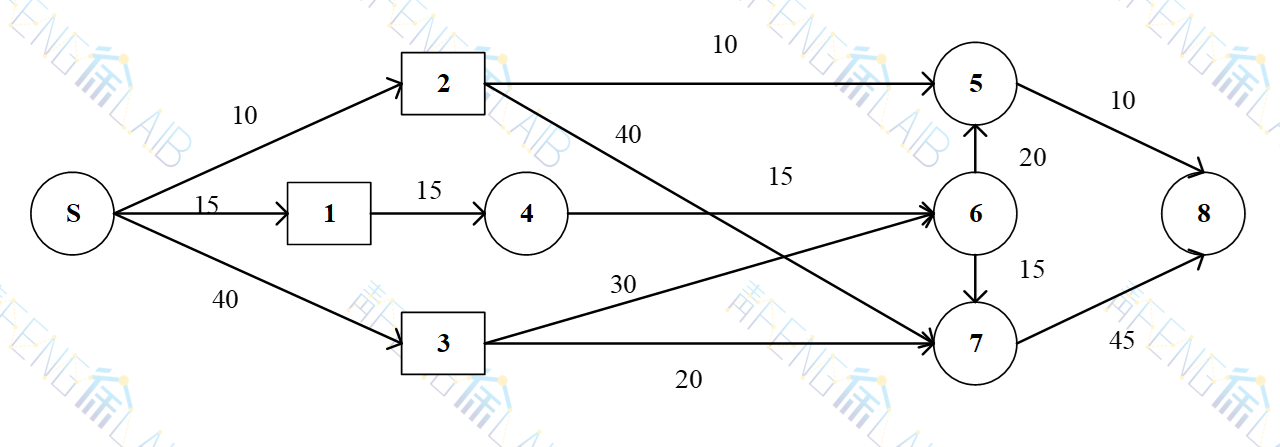
某地的电力公司有三个发电站,它们负责5个城市的供电任务,其输电网络如下图所示。由图可知,城市8由于经济发展,要求供应电力65MW,三个发电站在满足城市4、5、6、7的用电需要量后,它们还分别剩余15MW,10MW和40MW,输电网络剩余的输电能力见下图节点上的数字。三个发电站在满足城市4、5、6用电量之后,剩余发电能力共有65MW,与城市8的用电需求量刚好相等。问题是输电网络的输电能力是否满足输电65MW的电力,如不满足,需要增建哪些输电线路。

问题解析
根据上述对该问题的描述,可以转换成一个最大流的问题求解。图中的输电网络图有三个发点(即三个发电站),一个终点(城市8)。如果能求得从三个发点到终点的最大流,就知道输电网络的最大输电能力,也知道是哪些已饱和了的弧限制了输电能力的提高,从而可以据此确定应增建哪些输电线路。
问题求解
为了应用Ford-Fulkerson标号法求解上图所示的网络最大流,需要增设一个发点S,把网络图化为只有一个发点和一个终点的容量网络图,如下图所示。
应用Ford-Fulkerson标号法有如下表1所示的求解过程:

由上表可知最大流为55MW,最后的可行流见下图弧旁带括号的数值。

结果分析
从上图可知,城市8用电需求量为65MW,而输电网络的最大输电量只有55MW,相差10MW。为了增输10MW,最好的方案是在饱和弧⑤→⑧(最小割集上的弧)上增建输送10MW的新线路,而把非饱和弧S→③、⑥→⑤各增加10MW使之饱和,最后扩建方案如下图所示。如在饱和弧⑦→⑧上增建10MW的新线路,则还须把弧③→⑦扩容10MW。

04最小费用最大流问题
上一个例题求解的网络最大流问题只考虑了流的数量,没有考虑流的费用。在实际应用场景中,许多问题要考虑流的费用最小问题。本次小编选取一道天然气运输问题中的最小费用最大流问题,运用第80期详细介绍的方法进行求解。
例5
最小费用最大流问题
问题描述
中国石油天然气集团公司在东海有一个油气田(节点vs),该公司要将开采的天然气通过管道运送到上海的一个配送中心(节点vt),天然气在运送途中要经过管道更换接点(节点v2、v3、v4),换接前后的管道长短不一,而且不同的管道对应不同的单位流量费。下图是天然气运输的管道网络图,弧线表示管道,弧旁的数字(cij,dij)表示管道上的单位流量容量和费用。公司希望选择一个经济实惠的管道路线运输天然气,既运输最多的天然气又使总运输费用最少。

问题求解
从f(0)={0}开始,作L(f(0))如下图所示,用Dijkstra算法求得L(f(0))网络中的最短路为vs→v2→v3→vt,在网络G中相应的可增广链μ1={vs,v2,v3,vt}上用最大流算法进行调整:

结果见图

图 f(1)
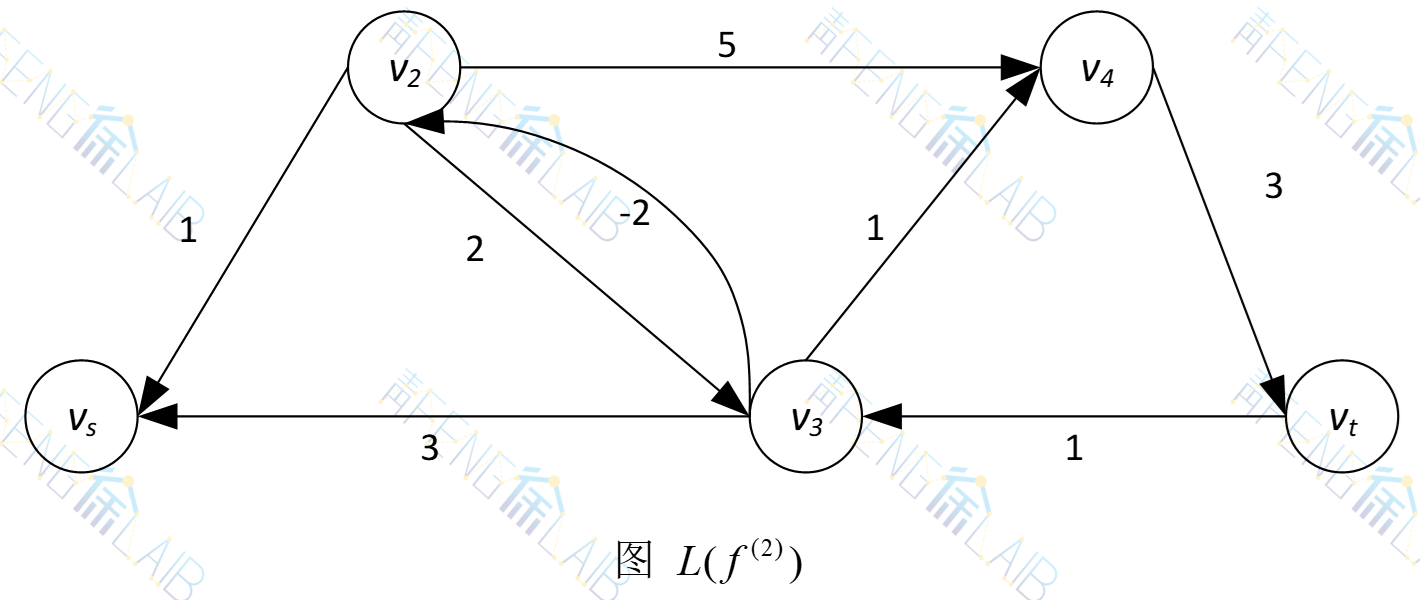
作L(f(1))如下图所示,由于边上有负权,所以求最短路不能用Dijkstra算法,可用逐次逼近法。最短路为vs→v3→vt,在网络G内相应的可增广链上进行调整,得流f(2),如下图所示。
W(f(2))=3,d(f(2))=2×1+2×2+3×1+1×3=12

作L(f(2))如下图所示,与vs关联的弧指向vs,不存在vs到vt的最短路。故下图所示的f(2)为最小费用最大流。费用为:
W(f(2))=3,d(f(2))=2×1+2×2+3×1+1×3=12
以上就是本期图与网络分析例题讲解的全部内容啦,通过对这一期的学习,相信大家一定能够加深对图与网络分析的理解,进而在生活实践中学会应用!
作者 | 陈志昂 林鑫
责编 | 刘文志
审核 | 徐小峰

·YUNCHOUSHUO·
·知乎|运筹说·
·简书|运筹说·
·CSDN|运筹说·
这篇关于运筹说 第81期 | 图与网络分析经典例题讲解的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!







