matlab|基于VMD-SSA-LSTM的多维时序光伏功率预测

本文主要是介绍matlab|基于VMD-SSA-LSTM的多维时序光伏功率预测，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

1 主要内容

变分模态分解(VMD)

麻雀搜索算法SSA

长短期记忆网络LSTM

2 部分代码

3 程序结果

4 下载链接

1 主要内容

之前分享了预测的程序基于LSTM的负荷和可再生能源出力预测【核心部分复现】，该程序预测效果比较好，并且结构比较清晰，但是仍然有同学咨询混合算法的预测，本次分享基于VMD-SSA-LSTM的多维时序光伏功率预测，本程序参考文章《基于VMD-SSA-LSSVM的短期风电预测》和《基于改进鲸鱼优化算法的微网系统能量优化管理》，采用不同方法混合嫁接的方式实现了光伏功率预测，对于预测而言，包括训练和测试，因此，该方法仍然可以用于风电、负荷等方面的预测。

变分模态分解(VMD)

VMD于2014年由Dragomiretskiy和Zosso提出，它的优点在于能根据不同情况确定分解模态个数，并能根据每个模态的最佳中心频率和有限带宽自适应和匹配，实现固有模

态分量的分解。相比EMD而言，VMD克服了EMD模态混叠和端点效应问题，并降低在复杂度高且非线性强的时间序列的非平稳性。

麻雀搜索算法SSA

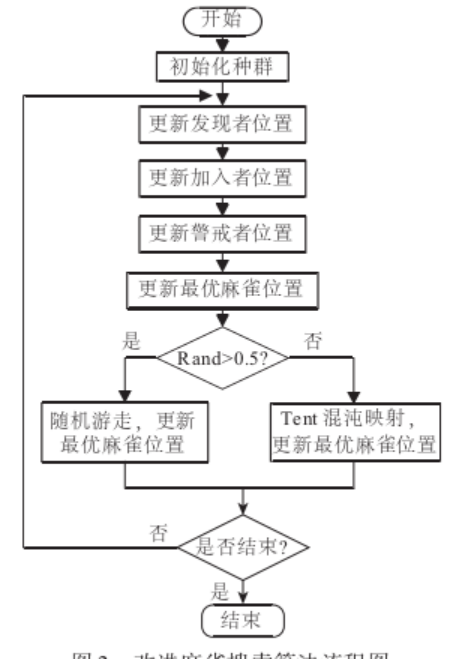
长短期记忆网络LSTM

长短期记忆网络(Long Short Term Memory, LSTM)作为一种特殊的循环神经网络(Recurrent neural network, RNN)，主要用于解决长序列训练过程中的梯度消失和梯度爆炸问题。

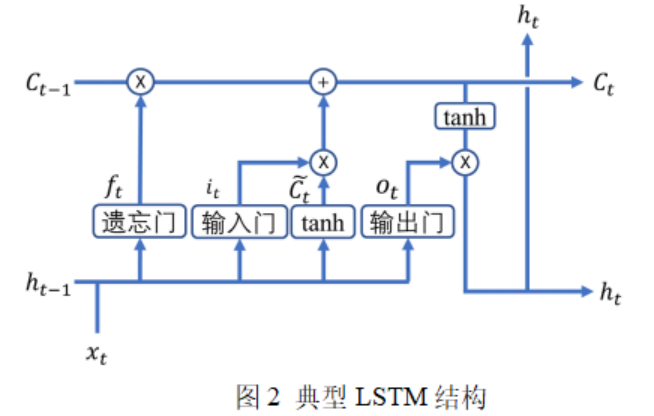
LSTM预测过程主要包括三个阶段：遗忘阶段，选择记忆阶段和输出阶段。遗忘阶段主要是对上一个节点传过来的信息进行选择性剔除，通过读取上一节点的输出状态和本节点的输出状态，由激活函数决定上一时刻细胞状态信息被遗忘的比例；选择记忆阶段是对输入的信息有选择性的进行筛选，将重要的信息挑选出来输入到当前细胞。选择记忆阶段主要包括两个步骤：第一步是输入层的激活函数决定哪些信息需要更新，层生成一个备选的更新内容，然后接下来是更新细胞状态。根据遗忘阶段的输出状态和备选更新的细胞状态来得到当前细胞的状态；输出阶段将会利用激活函数决定输出细胞状态的比例，然后将经过层处理的细胞状态与输出的细胞状态相乘得到最终的输出结果。

2 部分代码

% 指标计算
disp('训练集误差指标')
[mae5,rmse5,mape5,error5]=calc_error(T_train5,T_sim5);
fprintf('\n')

disp('测试集误差指标')
[mae6,rmse6,mape6,error6]=calc_error(T_test6,T_sim6);
fprintf('\n')
toc

%% VMD-SSA-LSTM预测
tic
disp('…………………………………………………………………………………………………………………………')
disp('VMD-SSA-LSTM预测')
disp('…………………………………………………………………………………………………………………………')

% SSA参数设置
pop=30; % 种群数量
Max_iter=10; % 最大迭代次数
dim=3; % 优化LSTM的3个参数
lb = [50,50,0.001];%下边界
ub = [300,300,0.01];%上边界
numFeatures=f_;
numResponses=outdim;
fobj = @(x) fun(x,numFeatures,numResponses,X) ;
[Best_pos,Best_score,curve,BestNet]=SSA(pop,Max_iter,lb,ub,dim,fobj);

% 绘制进化曲线
figure
plot(curve,'r-','linewidth',3)
xlabel('进化代数')
ylabel('均方根误差RMSE')
legend('最佳适应度')
title('SSA-LSTM的进化收敛曲线')

disp('')
disp(['最优隐藏单元数目为   ',num2str(round(Best_pos(1)))]);
disp(['最优最大训练周期为   ',num2str(round(Best_pos(2)))]);
disp(['最优初始学习率为   ',num2str((Best_pos(3)))]);

%% 对每个分量建模
for d=1:c
disp(['第',num2str(d),'个分量建模'])

X_imf=[X(:,1:end-1) imf(d,:)'];

%  重构数据集
for i = 1: num_samples - kim - zim + 1res(i, :) = [reshape(X_imf(i: i + kim - 1,:), 1, kim*or_dim), X_imf(i + kim + zim - 1,:)];
end


% 训练集和测试集划分
outdim = 1;                                  % 最后一列为输出
num_size = 0.7;                              % 训练集占数据集比例
num_train_s = round(num_size * num_samples); % 训练集样本个数
f_ = size(res, 2) - outdim;                  % 输入特征维度


P_train = res(1: num_train_s, 1: f_)';
T_train = res(1: num_train_s, f_ + 1: end)';
M = size(P_train, 2);

P_test = res(num_train_s + 1: end, 1: f_)';
T_test = res(num_train_s + 1: end, f_ + 1: end)';
N = size(P_test, 2);

%  数据归一化
[p_train, ps_input] = mapminmax(P_train, 0, 1);
p_test = mapminmax('apply', P_test, ps_input);

[t_train, ps_output] = mapminmax(T_train, 0, 1);
t_test = mapminmax('apply', T_test, ps_output);

%  格式转换
for i = 1 : M vp_train{i, 1} = p_train(:, i);vt_train{i, 1} = t_train(:, i);
end

for i = 1 : N vp_test{i, 1} = p_test(:, i);vt_test{i, 1} = t_test(:, i);
end

% 最佳参数的LSTM预测
layers = [ ...sequenceInputLayer(f_)              % 输入层lstmLayer(round(Best_pos(1)))      % LSTM层reluLayer                           % Relu激活层fullyConnectedLayer(outdim)         % 回归层regressionLayer];


options = trainingOptions('adam', ...                 % 优化算法Adam'MaxEpochs', round(Best_pos(2)), ...                            % 最大训练次数'GradientThreshold', 1, ...                       % 梯度阈值'InitialLearnRate', Best_pos(3), ...         % 初始学习率'LearnRateSchedule', 'piecewise', ...             % 学习率调整'LearnRateDropPeriod', round(Best_pos(2)*0.9), ...                   % 训练850次后开始调整学习率'LearnRateDropFactor',0.2, ...                    % 学习率调整因子'L2Regularization', 0.001, ...          % 正则化参数'ExecutionEnvironment', 'cpu',...                 % 训练环境'Verbose', 0, ...                                 % 关闭优化过程'Plots', 'training-progress');                    % 画出曲线

%  训练
net = trainNetwork(vp_train, vt_train, layers, options);
%  预测
t_sim7 = predict(net, vp_train); 
t_sim8 = predict(net, vp_test); 

%  数据反归一化
T_sim7_imf = mapminmax('reverse', t_sim7, ps_output);
T_sim8_imf = mapminmax('reverse', t_sim8, ps_output);

%  数据格式转换
T_sim7(d,:) = cell2mat(T_sim7_imf);% cell2mat将cell元胞数组转换为普通数组
T_sim8(d,:) = cell2mat(T_sim8_imf);
T_train7(d,:)= T_train;
T_test8(d,:)= T_test;
end

% 各分量预测的结果相加
T_sim7=sum(T_sim7);
T_sim8=sum(T_sim8);
T_train7=sum(T_train7);
T_test8=sum(T_test8);

% 指标计算
disp('训练集误差指标')
[mae7,rmse7,mape7,error7]=calc_error(T_train7,T_sim7);
fprintf('\n')

disp('测试集误差指标')
[mae8,rmse8,mape8,error8]=calc_error(T_test8,T_sim8);
fprintf('\n')
toc

%% 四种模型测试集结果绘图对比

figure;
plot(T_test2,'k','LineWidth',3);
hold on;
plot(T_sim2,'y','linewidth',3);
plot(T_sim6,'g','linewidth',3);
plot(T_sim8,'r','linewidth',3);
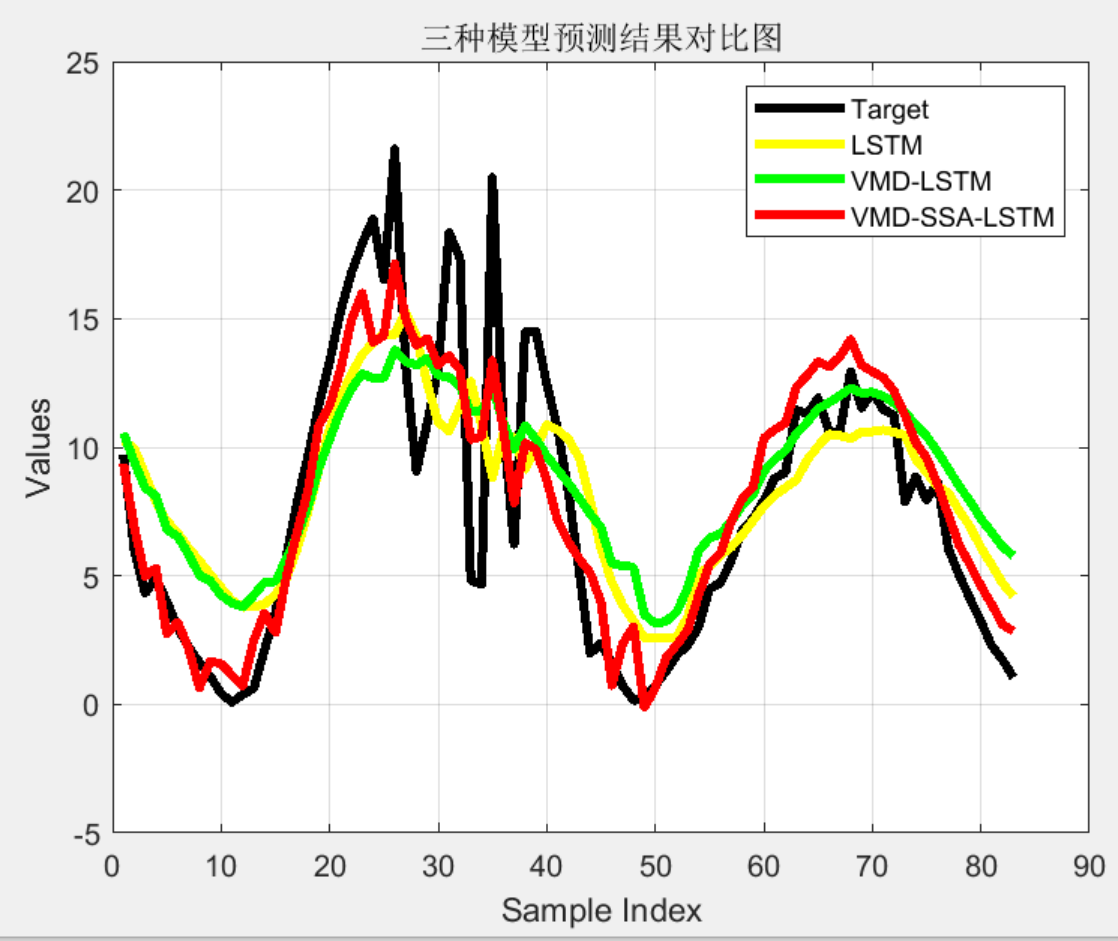
legend('Target','LSTM','VMD-LSTM','VMD-SSA-LSTM');
title('三种模型预测结果对比图');
xlabel('Sample Index');
ylabel('Values');
grid on;

figure
plot(error2,'k','linewidth',3);
hold on
plot(error6,'g','linewidth',3);
hold on
plot(error8,'r','linewidth',3);
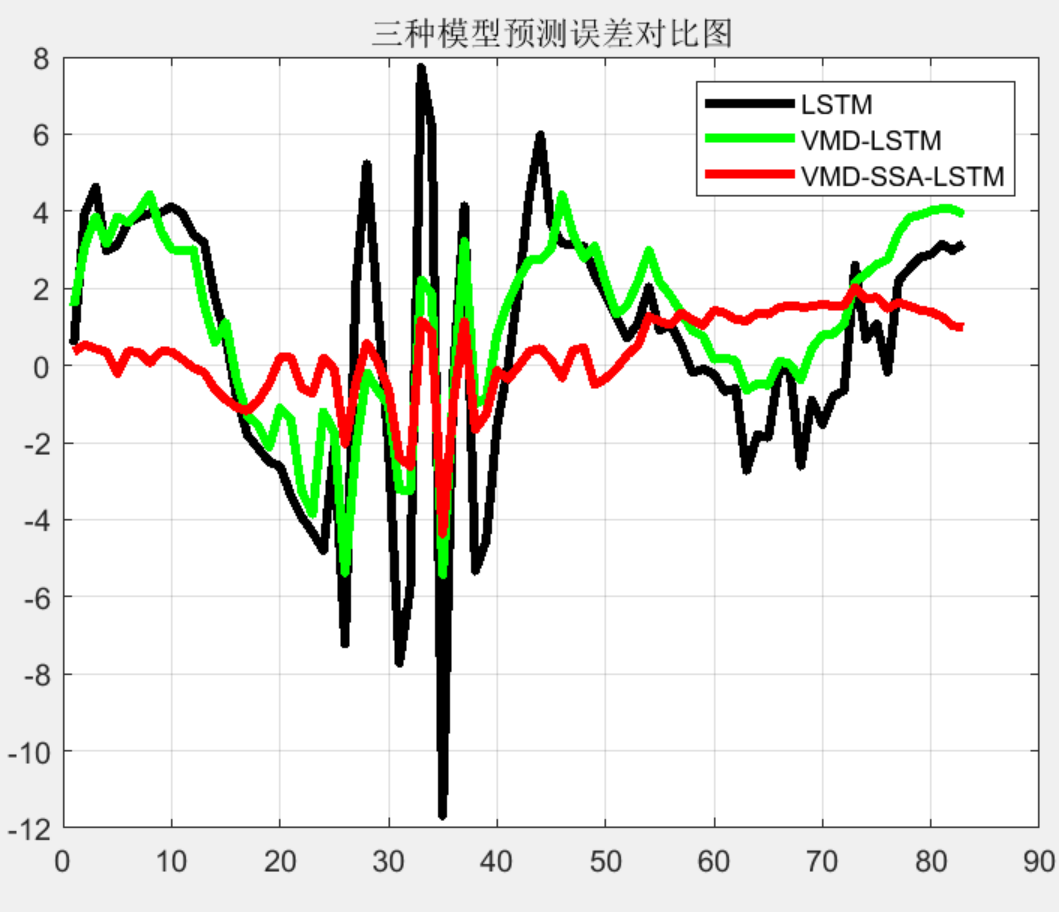
legend('LSTM','VMD-LSTM','VMD-SSA-LSTM');
title('三种模型预测误差对比图');
grid on;