本文主要是介绍【Codeforces Round 323 (Div 2)C】【观察找规律 STL map】GCD Table 从GCD矩阵中找出所有原始元素,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
#include<stdio.h>
#include<string.h>
#include<ctype.h>
#include<math.h>
#include<iostream>
#include<string>
#include<set>
#include<map>
#include<vector>
#include<queue>
#include<bitset>
#include<algorithm>
#include<time.h>
using namespace std;
void fre(){freopen("c://test//input.in","r",stdin);freopen("c://test//output.out","w",stdout);}
#define MS(x,y) memset(x,y,sizeof(x))
#define MC(x,y) memcpy(x,y,sizeof(x))
#define MP(x,y) make_pair(x,y)
#define ls o<<1
#define rs o<<1|1
typedef long long LL;
typedef unsigned long long UL;
typedef unsigned int UI;
template <class T1,class T2>inline void gmax(T1 &a,T2 b){if(b>a)a=b;}
template <class T1,class T2>inline void gmin(T1 &a,T2 b){if(b<a)a=b;}
const int N=505,M=0,Z=1e9+7,ms63=1061109567;
int casenum,casei;
int a[N][N];
int b[N*N];
int n,nn;
map<int,int>mop;
map<int,int>::iterator it;
int gcd(int x,int y)
{return y==0?x:gcd(y,x%y);
}
int main()
{while(~scanf("%d",&n)){mop.clear();for(int i=n*n;i;--i){scanf("%d",&b[i]);++mop[b[i]];}int p=0;map<int,int>::iterator tmp;for(it=mop.begin();it!=mop.end();it++)if(it->second&1){++p;a[p][p]=it->first;--it->second;for(int i=1;i<p;i++){int x=gcd(a[i][i],a[p][p]);a[i][p]=a[p][i]=x;mop[x]-=2;}}while(p<n){while(1){it=--mop.end();if(it->second==0)mop.erase(it);else break;}int x=it->first;++p;a[p][p]=x;--mop[x];for(int i=1;i<p;i++){int x=gcd(a[i][i],a[p][p]);a[i][p]=a[p][i]=x;mop[x]-=2;}}for(int i=1;i<=n;i++)printf("%d ",a[i][i]);puts("");}return 0;
}
/*
【trick&&吐槽】
做题没思路,从样例下手。【题意】
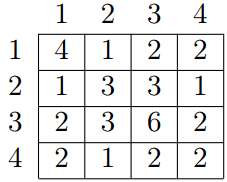
给你n([1,500])个数a[],b[i][j]表示gcd(a[i],a[j])
b[][]有n*n个数,我们把它打乱顺序,全部告诉你。
让你输出所有的a[]。【类型】
贪心 构造【分析】
这题很有趣。
一开始想很难想,完全不知道思考的方向。
这时候我们要怎么办?没错!观察样例!
我们发现,这个矩阵肯定是关于主对角线对称的。
于是我们先找到出现次数为奇数的数,这些数一定是位于主对角线上的,同时对应着一个a[]。
然后我们同时生成所有的gcd。
然而这样并不一定能把这个矩阵完全还原。
剩下的数的出现次数都可能为偶数。
这时我们发现,数值最大的数(还没被取),肯定在矩阵的主对角线。于是就放上去。
重复这个操作,就可以AC这道题啦!【时间复杂度&&优化】
O(n^2logn)【数据】
4
4 4 4 4 2 2 2 2
2 2 2 2 2 2 2 2*/这篇关于【Codeforces Round 323 (Div 2)C】【观察找规律 STL map】GCD Table 从GCD矩阵中找出所有原始元素的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!
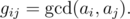
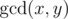 . For example, for array
. For example, for array