本文主要是介绍【VK Cup 2016 - Round 1 (Div 2 Edition)C】【构造】Bear and Forgotten Tree 3 构造一棵树直径为d且点1的深度为h,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
A tree is a connected undirected graph consisting of n vertices and n - 1 edges. Vertices are numbered 1 through n.
Limak is a little polar bear and Radewoosh is his evil enemy. Limak once had a tree but Radewoosh stolen it. Bear is very sad now because he doesn't remember much about the tree — he can tell you only three values n, d and h:
- The tree had exactly n vertices.
- The tree had diameter d. In other words, d was the biggest distance between two vertices.
- Limak also remembers that he once rooted the tree in vertex 1 and after that its height was h. In other words, h was the biggest distance between vertex 1 and some other vertex.
The distance between two vertices of the tree is the number of edges on the simple path between them.
Help Limak to restore his tree. Check whether there exists a tree satisfying the given conditions. Find any such tree and print its edges in any order. It's also possible that Limak made a mistake and there is no suitable tree – in this case print "-1".
The first line contains three integers n, d and h (2 ≤ n ≤ 100 000, 1 ≤ h ≤ d ≤ n - 1) — the number of vertices, diameter, and height after rooting in vertex 1, respectively.
If there is no tree matching what Limak remembers, print the only line with "-1" (without the quotes).
Otherwise, describe any tree matching Limak's description. Print n - 1 lines, each with two space-separated integers – indices of vertices connected by an edge. If there are many valid trees, print any of them. You can print edges in any order.
5 3 2
1 2 1 3 3 4 3 5
8 5 2
-1
8 4 2
4 8 5 7 2 3 8 1 2 1 5 6 1 5
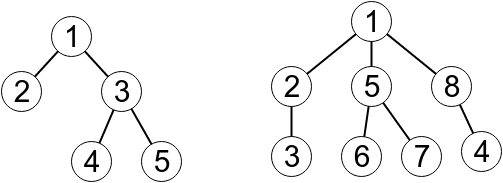
Below you can see trees printed to the output in the first sample and the third sample.
#include<stdio.h>
#include<iostream>
#include<string.h>
#include<string>
#include<ctype.h>
#include<math.h>
#include<set>
#include<map>
#include<vector>
#include<queue>
#include<bitset>
#include<algorithm>
#include<time.h>
using namespace std;
void fre() { freopen("c://test//input.in", "r", stdin); freopen("c://test//output.out", "w", stdout); }
#define MS(x,y) memset(x,y,sizeof(x))
#define MC(x,y) memcpy(x,y,sizeof(x))
#define MP(x,y) make_pair(x,y)
#define ls o<<1
#define rs o<<1|1
typedef long long LL;
typedef unsigned long long UL;
typedef unsigned int UI;
template <class T1, class T2>inline void gmax(T1 &a, T2 b) { if (b>a)a = b; }
template <class T1, class T2>inline void gmin(T1 &a, T2 b) { if (b<a)a = b; }
const int N = 1e5 + 10, M = 0, Z = 1e9 + 7, ms63 = 0x3f3f3f3f;
int n, h, d;
int a[N];
bool solve()
{if (h < (d + 1) / 2)return 0; //必须有h>=(d+1)/2if (h > d)return 0; //必须有h<=dif (n > 2 && d == 1)return 0; //当n>2时必有d>2for (int i = 1; i <= d + 1; ++i)a[i] = i;swap(a[1], a[1 + h]);for (int i = 1; i <= d; ++i)printf("%d %d\n", a[i], a[i + 1]);int p = 1 + d / 2;for (int i = d + 2; i <= n; ++i)printf("%d %d\n", a[p], i);return 1;
}
int main()
{while (~scanf("%d%d%d", &n, &d, &h)){if (!solve())puts("-1");}return 0;
}
/*
【题意】
让你构造一棵树,使其满足——
1,有n(1e5)个节点
2,树的直径为d
3,距离节点1最远的点的距离为h【类型】
贪心 构造【分析】
我们直接从贪心的角度入手做构造就好啦。
只要d>=h>=(d+1)/2即可成功构造
唯一的反例是d==h==1且点数超过2的时候,这个特判一下即可。构造方法:
首先,我们构造一条长度为d的链,作为这棵树的直径
然后,我们使得节点1这这条链上,距离一端的位置恰好为h
至于剩下的节点,全部连在直径中间的位置即可。【时间复杂度&&优化】
O(n)*/这篇关于【VK Cup 2016 - Round 1 (Div 2 Edition)C】【构造】Bear and Forgotten Tree 3 构造一棵树直径为d且点1的深度为h的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!



