OO_BUAA_Unit1

第一单元_表达式解析

前言

本次作业要求对一个表达式进行化简，之后增加了对三角函数，嵌套括号，自定义函数以及求导的迭代。

homework1

设计思路

本次作业我使用了递归下降法进行对表达式的解析，首先通过使用Preteat类对表达式进行预处理，通过对层层解析，当解析得到某个变量对象后使用Expr.addExpr(Factor)或Term.addTerm(Factor)将其返回到其父类。最后通过Output类进行多项式的输出。

递归下降法分析表达式主要是通过Parser(语法分析器)与Lexer(词法分析器)进行逐个字符的解析，其与常规的整体分析表达式的区别在于边读边解析，解决了递归层数较多时整体分析法容易陷入混乱的问题

public class Parser {public Expr parserExpr() {Expr expr = new Expr();expr.addTerm(parserTerm());while (lexer.getCurToken().equals("+") || lexer.getCurToken().equals("-")) {expr.addTerm(parserTerm());}return expr;}public Term parserTerm() {Term term = new Term();Factor factor = parserFactor();term.addFactor(factor);while (lexer.getCurToken().equals("*")) {lexer.next();term.addFactor(parserFactor());}return term;}public Factor parserFactor() {if (lexer.getCurToken().equals("(")) {//解析Expr因子} else {Num num = lexer.getNum();Pow pow = lexer.getPow();if (num != null) {//解析Num因子} else if (pow != null) {//解析Pow因子} else {return null;}}}
}

除此之外，本次作业另外存在的一个难点在于对变量类的构造，我大约想出了以下几点以适应我的思路。

• 对于变量的分类,本次作业的主要变量类型有Expr,Term与Factor三种类型，其中Factor有三种类型Num(常数因子),Pow(幂函数因子)与Expr(表达式因子)，故自然想到了利用接口interface Factor来实现变量类。

• 对于变量类的具体实现，关键在于变量类的数据结构。

对于Pow

$$Pow=x^{inde{x}_1}\ast y^{inde{x}_2}\ast z^{inde{x}_3}$$

对于Num

$$Num=num(num!=0)$$

对于Expr(表达式),Term(项)的本质分析，本质上均为

$$Expr=\sum x^{inde{x}_1}\ast y^{inde{x}_2}\ast z^{inde{x}_3}\ast num=\sum Pow+\sum Num=\sum BigInteger\ast Factor$$

$$Term=\sum x^{inde{x}_1}\ast y^{inde{x}_2}\ast z^{inde{x}_3}\ast num=\sum Pow+\sum Num=\sum BigInteger\ast Factor$$

考虑到上述数学公式，各种变量类的容器也就自然了，我采用的是

public class Num implements Factor {private BigInteger num;}
public class Pow implements Factor {private HashMap<String, BigInteger> hashMap;}
public class Expr implements Factor {private HashMap<Factor, BigInteger> hashMap;//BigInteger是系数}
public class Term implements Factor {private HashMap<Factor, BigInteger> hashMap;//BigInteger是系数}

除此之外，我还设立了Output类用以对各个对象进行字符串输出与化简，Pretreat类用以预处理

大概的几个基本的难点就搞定了，下面是我的类图

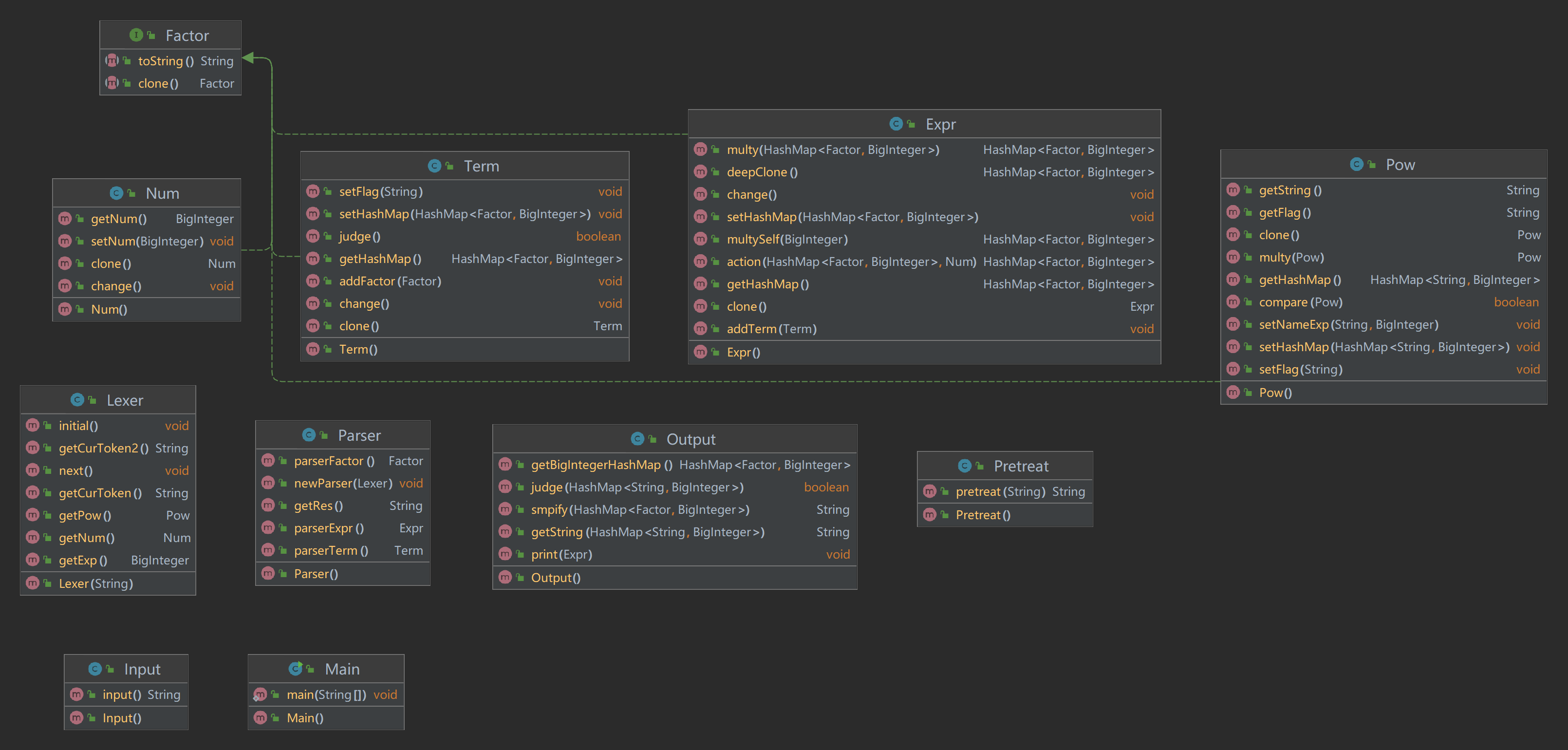
UML图

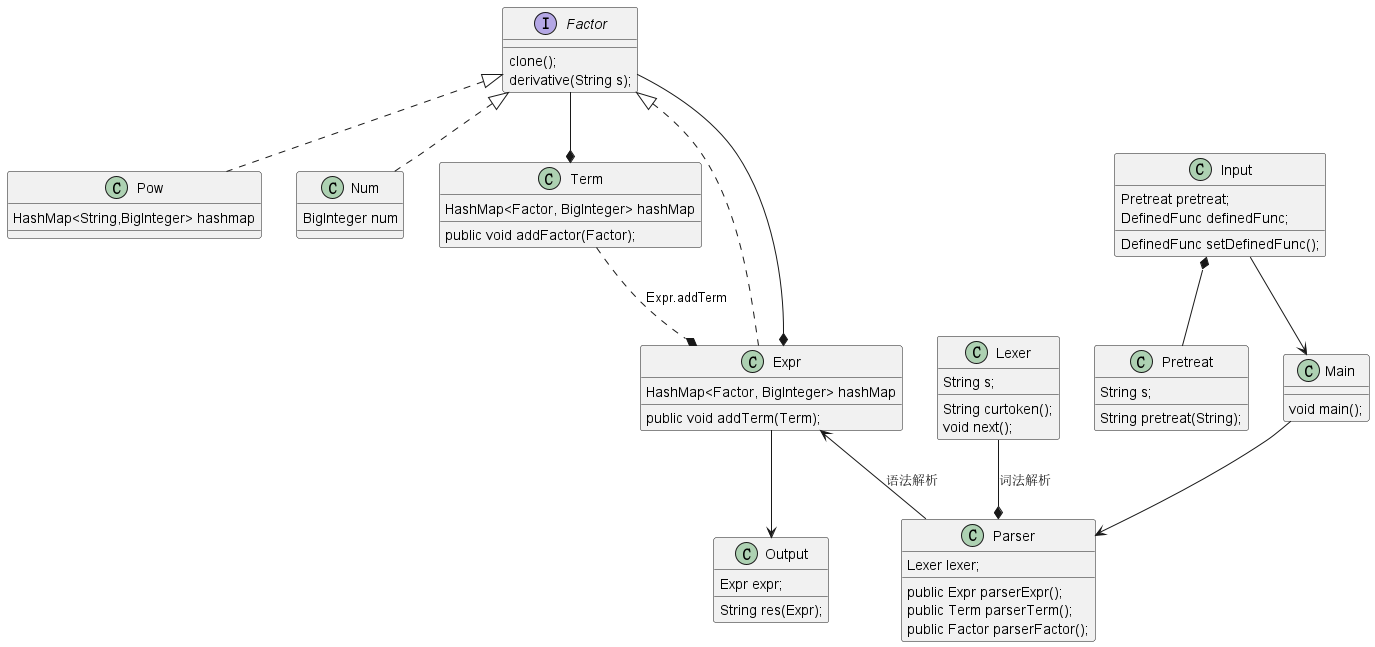
优化方法

我的优化主要在两个方面：

• 在Expr.addExpr(Factor factor)方法中，优先合并同类项，其次再考虑将factor中的Pow或Num加入到hashmap中
• 在Output方法作出最终输出时，优先考虑将系数大于0的Pow或Num输出得，同时将x**2优化为x*x

Bug分析

中强测

由于对HashMap的机制还是不熟悉，在使用迭代器的时候出现了一个bug，在遍历HashMap的时候忘记了及时更改已经变化的值，在较为复杂的计算中会出现系数未被更新的现象，很快就能修好

互测

因为房间等级不高，互测我成功hack了19次，主要是手捏测试数据和阅读源代码发现漏洞，包括但不限于：

• 在进行复杂式子计算时，系数相加时两个加数有问题

• 0**0处理不到位

• 合并同类项时忘记考虑符号

• 多项式相乘得到的次数系数不正确

体会心得

在第一次作业的过程中我感受到了递归下降法的强大威力，竟然可以轻松的解决复杂式子的分析。同时感受到了一个好的架构往往可以事半功倍，因为第一次作业的框架拓展性还好，后两次作业也没有进行重构，迭代的难度也算不上太大。总之是颇有收获的一次作业。

homework2

迭代要求

本次作业增加了自定义函数和三角函数，文法定义如下

迭代思路

首先是对自定义函数的解析，这时有两种处理情况，提前解析，之后方便代入，或者先代入，后解析，我采用的是第一种思路，但是由于规则中对不调用的f,g,h函数不计入cost的计算，此时第一种思路在互测可能会出现大问题。但是在大多数情况下还是好用的，我的大概思路是通过设定新的Parser和Lexer用来解析好表达式，将其存入一个DefinedFunc对象中，在之后对主Expr解析时调用，而对于自定义函数的具体计算我主要采用的时replaceAll()方法，但是如果在函数解析的过程中没有将x,y,z进行替换或者计算时同时将所有形参代入在这样的情况下会出现bug

1
f(x,y) = x + y
f(y,2)
//先代入y,再代入2
f(y,2) -> y + y -> 2+2 = 4
//同时代入
f(y,2) -> y + 2
//在解析的过程中使用其他字母替代
f(p,q) = p + q
f(y,2) -> y+q -> y+2

其次是三角函数的引入，三角函数的基本形式是sin(Factor)/cos(Factor)由于三角函数的引入，除了常规的TrigonoFunc，还会有Pow和TrigonoFUnc的混合类
$$Mixture=\prod \sin (Factor{)}^{index1}\ast \prod \cos (Factor{)}^{index2}\ast Pow$$

于是我引入了Mixture类用来记录多项式中的此类型变量，使用容器

public class Mixture implements Factor {private HashMap<TrigonoFunc, BigInteger> hashMap;private Pow pow;}

最后本次作业的新的要求是要求支持嵌套括号，由于第一次作业递归下降的框架，嵌套括号在第一次作业就已经支持，所以这不是问题。

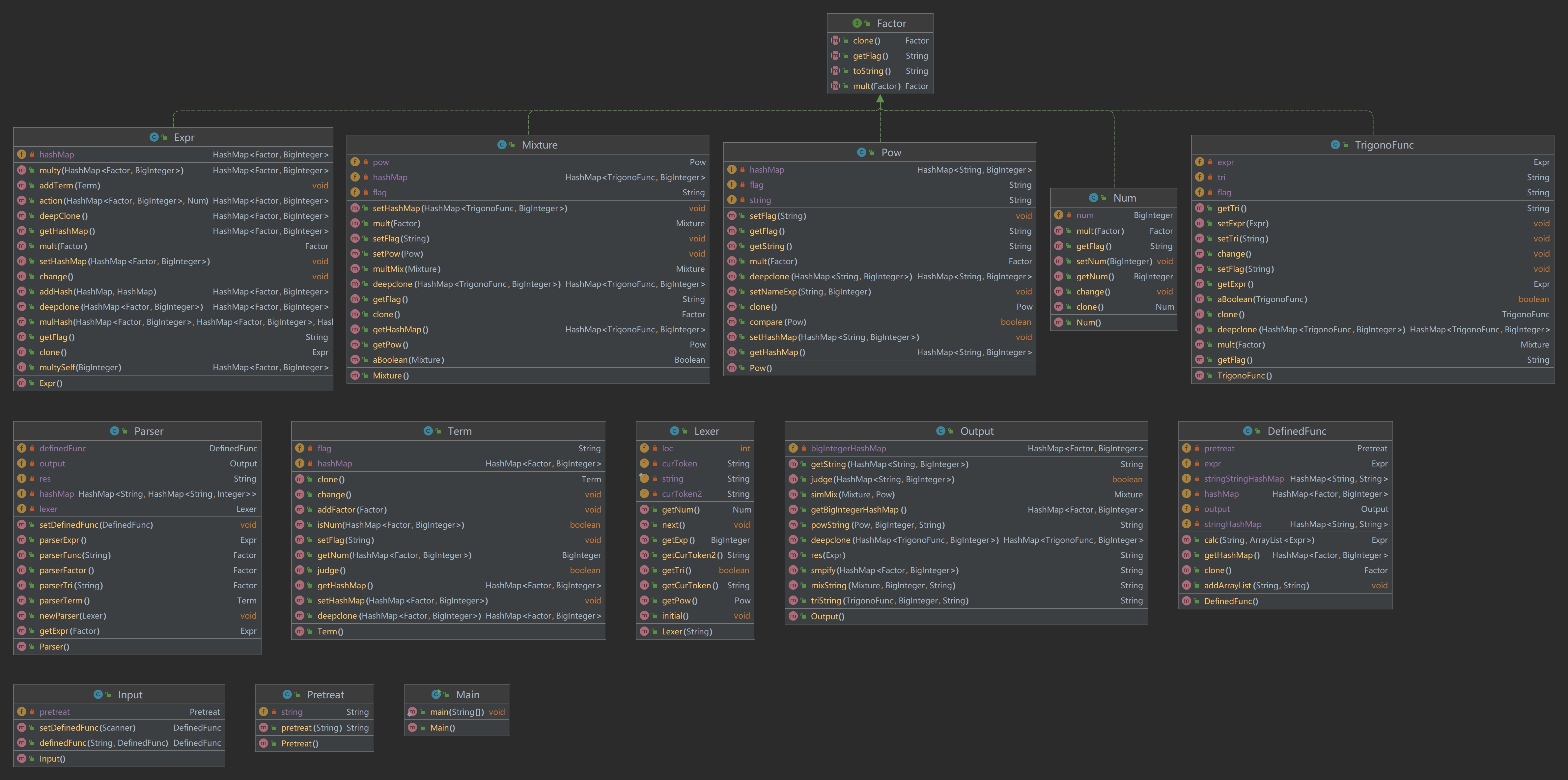
UML图

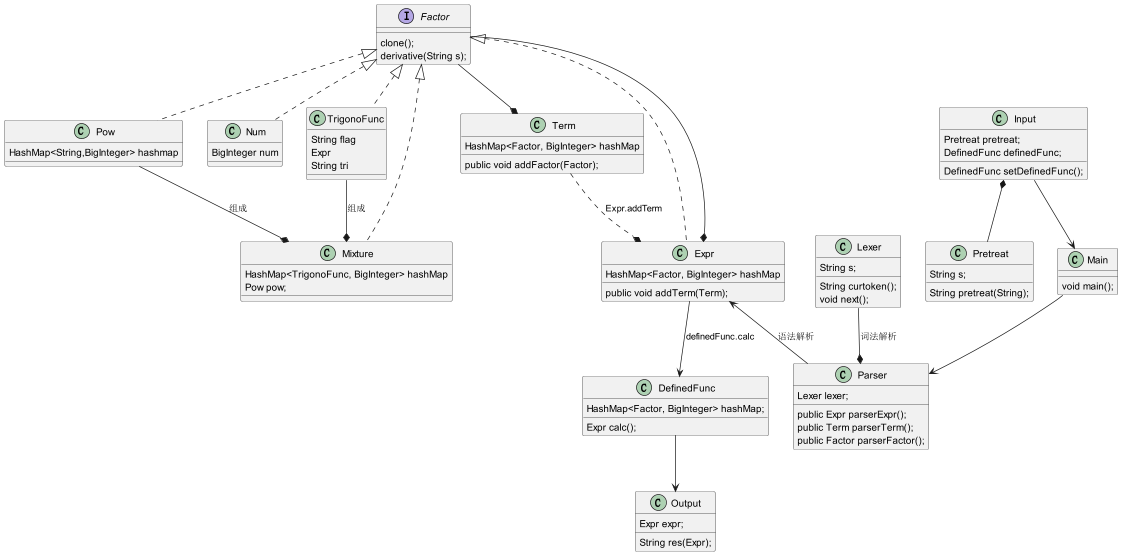
优化方法

关于三角函数主要有两种优化方式:合并同类项，和 $\sin (expr{)}^2+\cos (expr{)}^2=1$，我只做了第一个优化，但是我注意到由于我在Mixsure类中使用的数据结构是HashMap所以遍历起来很麻烦而且可能有一些多余的同类项没有合并导致我合并同类项没有做到完全合并，而且在优化的过程中发现了重大的bug，优化相当于半途而废，没有完全写完，本次的优化做的并不好。

Bug分析

构造过程的bug

首先就是我在周六下午进行测试时发现的bug,由于框架的可拓展性还好，我的每次迭代只需要大概一下午的时间就可以完成，我的中测和弱测很轻松就通过了，但在周六下午我进行了一些有关于Mixture类的高次(三次及以上)计算，突然发现了巨大的问题，在输出时大量的Factor的HashMap都变成了Null，这时我感受到了巨大的压力，此时距离作业提交只剩下不到十八小时，于是我开始大量构造样例去测试，发现我出错的样例缺乏明显的规律而且在越复杂的时候越可能出现bug，于是我对样例进行了长时间的单步调试，发现在expr与expr进行计算时某些无关HashMap发生了变化，此时我感受到了一种可能性——深克隆，在查阅资料之后，我发现在我之前的部分.clone()方法出现了浅克隆的现象，主要是在java自带的HashMap.clone()方法，于是我进行了bug的修复，并再一次进行了较大量的测试，再次完成了提交，此时已经是深夜三四点了(悲)

强测与互测

强测过程中我出现了一个bug，在Mixture与Mixture乘法时Pow部分的乘法在其中一个为NULL时出现了小问题，在较为复杂的运算时可能出现问题，是我考虑不周而且测试不够的问题，加一行就可以解决。

互测过程中也有一个bug，我在Pretreat方法中的预处理环节对于+++和---这两种情况缺乏处理，我在Pretreat方法中加两行就可以解决

找到别人的bug:对sin(0)带前导符号的次幂处理不周。

homework3

迭代思路

这次是我迭代用时最少的一次，也是很寄很寄的一次(还是缺乏测试)，主要是对各个变量类增加了public Expr derivative(String s)方法，对于Num类，直接返回Num(0),对于Pow类，也是返回一个简单操作的Pow*Num对象即可，但是我在考虑到复合函数和Mixture求导的情况注意到，返回的对象还是为Expr最好，因为Pow的求导甚至都有系数，而将返回的类型设置为Term没有任何优越性，Term本质上还是Expr的一种子类，拥有其所有性质。而对于乘法法则和嵌套函数的求导，我考虑进行递归下降法解析求导，注意到我的方法几乎随时都在进行拆括号以及化简，除了sin/cos基本不会出现嵌套函数或者乘法原则

下面是对乘法原则的一定程度的还原

public Expr derivativetri(String s) {Mixture mixture1 = new Mixture();mixture1.setHashMap(hashMap2);Mixture mixture2 = new Mixture();mixture2.setHashMap(hashMap1);Term term = new Term();term.addFactor(mixture1.derivative(s));term.addFactor(mixture2);Term term1 = new Term();term1.addFactor(mixture1);term1.addFactor(mixture2.derivative(s));Expr expr = new Expr();expr.addTerm(term);expr.addTerm(term1);return expr;
}

下面是嵌套原则

public Expr derivative(String s) {TrigonoFunc trigonoFunc = new TrigonoFunc();trigonoFunc = this.clone();TrigonoFunc trigonoFunc1 = new TrigonoFunc();trigonoFunc1.setExpr(this.getExpr());if (trigonoFunc.getTri().equals("sin")) {trigonoFunc1.setTri("cos");trigonoFunc1.setFlag(flag);} else {trigonoFunc1.setTri("sin");if (flag.equals("+")) {trigonoFunc1.setFlag("-");} else {trigonoFunc1.setFlag("+");}}Expr expr1 = expr.derivative(s);Term term = new Term();term.addFactor(trigonoFunc1);term.addFactor(expr1);if (!term.judge()) {term.change();}Expr expr2 = new Expr();expr2.addTerm(term);return expr2;}

优化方法

优化的方法和第二次作业基本一致，我没有做多余的优化，为了保证正确性

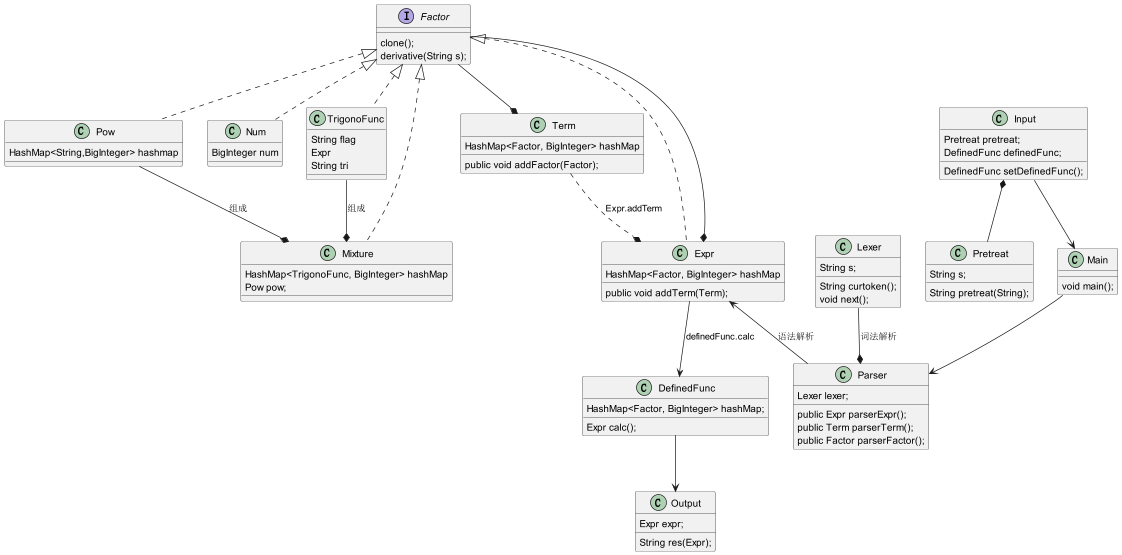
类图

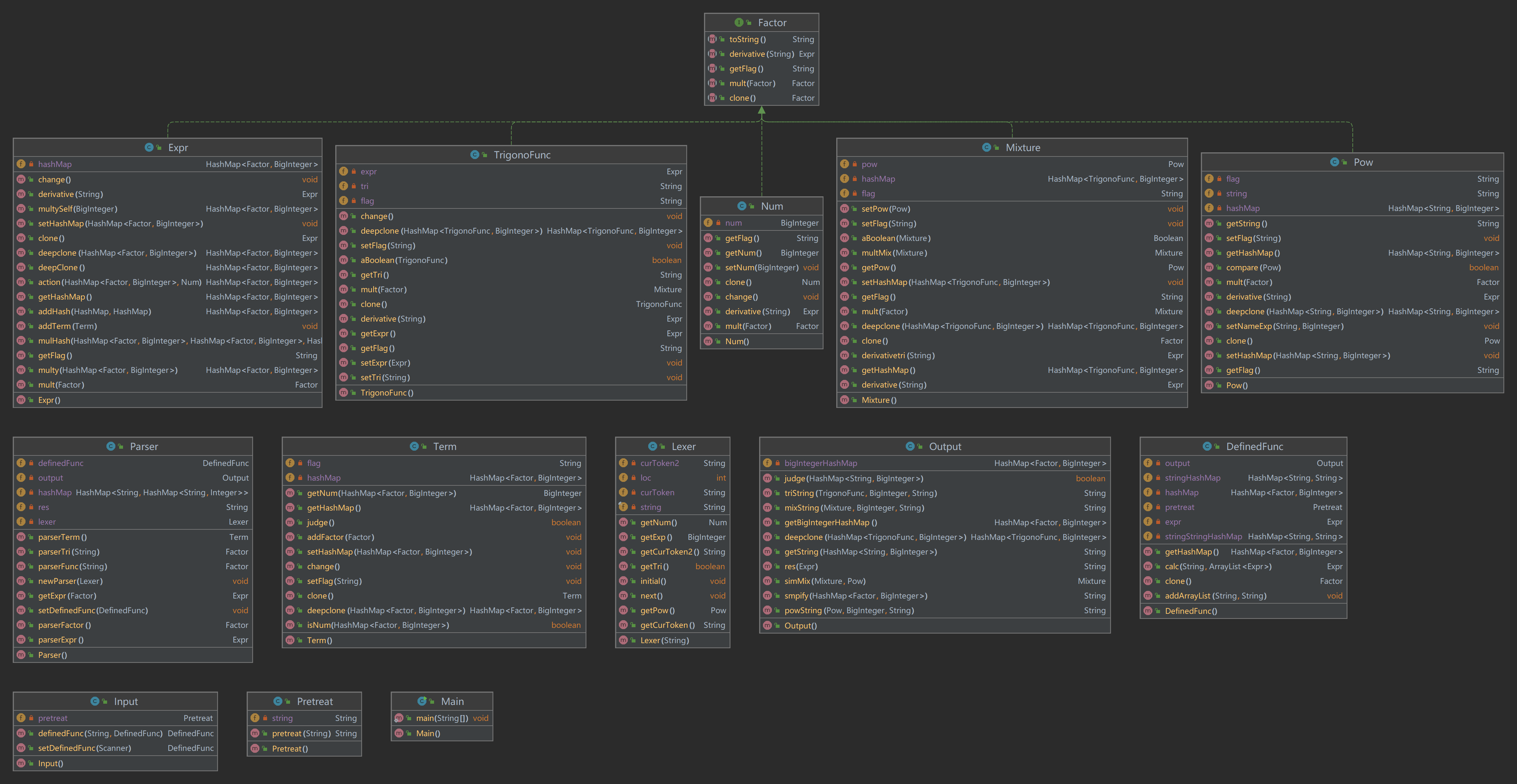
UML图与hw2基本一致，没有新增的类，只是Factor增加了derivative方法

bug分析

构建过程

在构建的过程中没有出现太多困难或者其他bug，但是在强测中出现了巨大问题

强测，互测

强测中出现了一个非常弱智的bug，我直接忘记了dx(expr)前导符号位-的情况，强测挂了三个点，但互测中意外的没怎么被发现

互测中没有发现别人的bug

复杂度分析

Cogc:认知复杂度，是由sonarQube设计的一个算法，算法将一段程序代码被理解的复杂程度，估算成一个整数——可以等同于代码的理解成本。

ev(G) 基本复杂度是用来衡量程序非结构化程度的，非结构成分降低了程序的质量，增加了代码的维护难度，使程序难于理解。因此，基本复杂度高意味着非结构化程度高，难以模块化和维护。实际上，消除了一个错误有时会引起其他的错误。

iv(G) 模块设计复杂度是用来衡量模块判定结构，即模块和其他模块的调用关系。软件模块设计复杂度高意味模块耦合度高，这将导致模块难于隔离、维护和复用。模块设计复杂度是从模块流程图中移去那些不包含调用子模块的判定和循环结构后得出的圈复杂度，因此模块设计复杂度不能大于圈复杂度，通常是远小于圈复杂度。

V(G):是用来衡量一个模块判定结构的复杂程度，数量上表现为独立路径的条数，即合理的预防错误所需测试的最少路径条数，圈复杂度大说明程序代码可能质量低且难于测试和维护，经验表明，程序的可能错误和高的圈复杂度有着很大关系。

Method	CogC	ev(G)	iv(G)	v(G)
“DefinedFunc.addArrayList(String,String)”	5	1	4	4
“DefinedFunc.calc(String,ArrayList)”	1	1	2	2
DefinedFunc.clone()	0	1	1	1
DefinedFunc.getHashMap()	0	1	1	1
“Expr.action(HashMap<Factor,BigInteger>,Num)”	7	1	6	6
“Expr.addHash(HashMap,HashMap)”	5	1	5	5
Expr.addTerm(Term)	14	2	14	15
Expr.change()	3	1	3	3
Expr.clone()	0	1	1	1
Expr.deepClone()	0	1	1	1
“Expr.deepclone(HashMap<Factor,BigInteger>)”	1	1	2	2
Expr.derivative(String)	1	1	2	2
Expr.getFlag()	0	1	1	1
Expr.getHashMap()	0	1	1	1
“Expr.mulHash(HashMap<Factor,BigInteger>,HashMap<Factor,BigInteger>,HashMap<Factor,BigInteger>)”	22	1	7	7
Expr.mult(Factor)	0	1	1	1
“Expr.multy(HashMap<Factor,BigInteger>)”	16	1	16	16
Expr.multySelf(BigInteger)	2	2	3	3
“Expr.setHashMap(HashMap<Factor,BigInteger>)”	0	1	1	1
“Input.definedFunc(String,DefinedFunc)”	0	1	1	1
Input.setDefinedFunc(Scanner)	1	1	2	2
Lexer.Lexer(String)	0	1	1	1
Lexer.getCurToken()	0	1	1	1
Lexer.getCurToken2()	0	1	1	1
Lexer.getExp()	1	1	2	2
Lexer.getNum()	18	5	8	8
Lexer.getPow()	6	3	3	5
Lexer.getTri()	0	1	1	1
Lexer.initial()	1	1	2	2
Lexer.next()	4	2	3	3
Main.main(String[])	0	1	1	1
Mixture.aBoolean(Mixture)	31	8	12	14
Mixture.clone()	0	1	1	1
“Mixture.deepclone(HashMap<TrigonoFunc,BigInteger>)”	1	1	2	2
Mixture.derivative(String)	2	2	2	2
Mixture.derivativetri(String)	7	3	4	4
Mixture.getFlag()	0	1	1	1
Mixture.getHashMap()	0	1	1	1
Mixture.getPow()	0	1	1	1
Mixture.mult(Factor)	13	4	8	8
Mixture.multMix(Mixture)	21	1	13	13
Mixture.setFlag(String)	0	1	1	1
“Mixture.setHashMap(HashMap<TrigonoFunc,BigInteger>)”	0	1	1	1
Mixture.setPow(Pow)	0	1	1	1
Num.change()	0	1	1	1
Num.clone()	0	1	1	1
Num.derivative(String)	0	1	1	1
Num.getFlag()	0	1	1	1
Num.getNum()	0	1	1	1
Num.mult(Factor)	0	1	1	1
Num.setNum(BigInteger)	0	1	1	1
“Output.deepclone(HashMap<TrigonoFunc,BigInteger>)”	1	1	2	2
Output.getBigIntegerHashMap()	0	1	1	1
“Output.getString(HashMap<String,BigInteger>)”	7	1	4	5
“Output.judge(HashMap<String,BigInteger>)”	3	3	2	3
“Output.mixString(Mixture,BigInteger,String)”	16	1	9	13
“Output.powString(Pow,BigInteger,String)”	7	1	4	5
Output.res(Expr)	16	1	9	10
“Output.simMix(Mixture,Pow)”	16	1	10	10
“Output.smpify(HashMap<Factor,BigInteger>)”	20	4	13	15
“Output.triString(TrigonoFunc,BigInteger,String)”	7	1	6	8
Parser.getExpr(Factor)	3	1	3	3
Parser.newParser(Lexer)	0	1	1	1
Parser.parserExpr()	2	1	3	3
Parser.parserFactor()	26	7	14	14
Parser.parserFunc(String)	22	4	11	11
Parser.parserTerm()	2	1	3	3
Parser.parserTri(String)	25	6	11	12
Parser.setDefinedFunc(DefinedFunc)	0	1	1	1
Pow.clone()	0	1	1	1
Pow.compare(Pow)	0	1	1	1
“Pow.deepclone(HashMap<String,BigInteger>)”	1	1	2	2
Pow.derivative(String)	8	5	6	6
Pow.getFlag()	0	1	1	1
Pow.getHashMap()	0	1	1	1
Pow.getString()	0	1	1	1
Pow.mult(Factor)	9	2	4	4
Pow.setFlag(String)	0	1	1	1
“Pow.setHashMap(HashMap<String,BigInteger>)”	0	1	1	1
“Pow.setNameExp(String,BigInteger)”	0	1	1	1
Pretreat.pretreat(String)	0	1	1	1
Term.addFactor(Factor)	25	2	10	11
Term.change()	3	1	3	3
Term.clone()	0	1	1	1
“Term.deepclone(HashMap<Factor,BigInteger>)”	1	1	2	2
Term.getHashMap()	0	1	1	1
“Term.getNum(HashMap<Factor,BigInteger>)”	2	2	2	2
“Term.isNum(HashMap<Factor,BigInteger>)”	1	1	3	3
Term.judge()	0	1	1	1
Term.setFlag(String)	0	1	1	1
“Term.setHashMap(HashMap<Factor,BigInteger>)”	0	1	1	1
TrigonoFunc.aBoolean(TrigonoFunc)	1	2	2	2
TrigonoFunc.change()	0	1	1	1
TrigonoFunc.clone()	0	1	1	1
“TrigonoFunc.deepclone(HashMap<TrigonoFunc,BigInteger>)”	1	1	2	2
TrigonoFunc.derivative(String)	6	1	4	4
TrigonoFunc.getExpr()	0	1	1	1
TrigonoFunc.getFlag()	0	1	1	1
TrigonoFunc.getTri()	0	1	1	1
TrigonoFunc.mult(Factor)	9	1	6	6
TrigonoFunc.setExpr(Expr)	0	1	1	1
TrigonoFunc.setFlag(String)	0	1	1	1
TrigonoFunc.setTri(String)	0	1	1	1

Class	OCavg	OCmax	WMC
DefinedFunc	2.00	4	8
Expr	3.07	8	46
Input	1.50	2	3
Lexer	2.22	6	20
Main	1.00	1	1
Mixture	3.23	11	42
Num	1.00	1	7
Output	5.80	12	58
Parser	5.75	13	46
Pow	1.73	5	19
Pretreat	1.00	1	1
Term	2.40	11	24
TrigonoFunc	1.83	6	22

下面是一些超标的方法

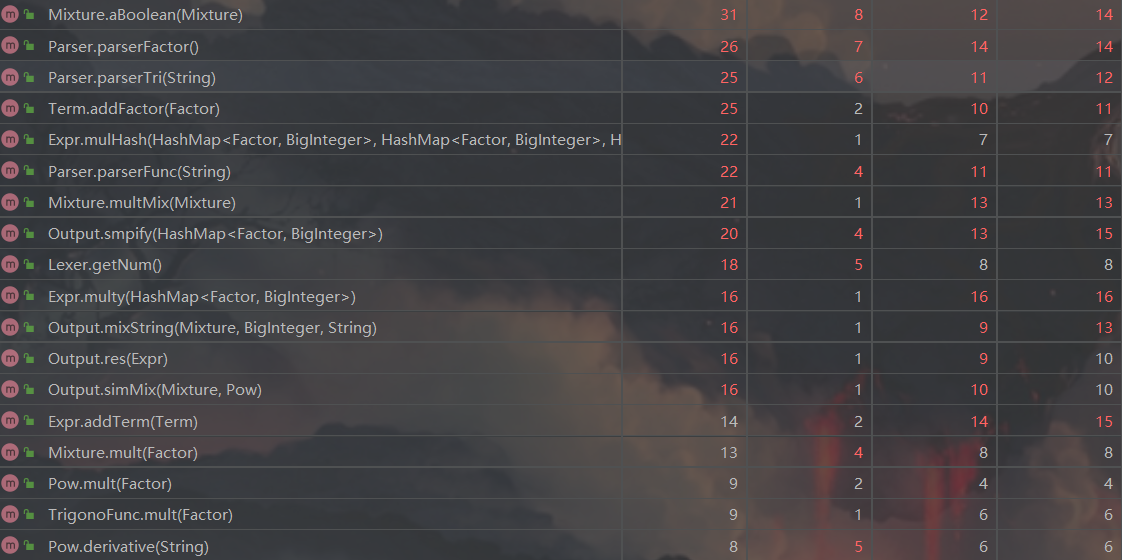
可以注意到Mixture类判断同类项的方法，Parser的解析方法,出现复杂度较高的方法都有着大量遍历或者不断解析新字符串的特点，因为我很多地方其实都有冗余的代码，自己又懒得改，复杂度高其实也是正常，之后应该尝试降低代码复杂度

总结

从结果来看，第一次作业是不成功的，三次强测都出现了错误，但是在学习的过程中，我深刻感受到了面向对象与面向过程之间的差异:只需要让每个部分做自己的事情。

除此之外，还有就是测试的重要性，第一次强测前，我只进行了小部分的手捏数据测试，自认为遍历了大部分可能，却忽略了在复杂式子时迭代器的缺陷导致强测直接暴死，第二次强测之前进行了较多次数的测试，发现了深克隆这一重要的Bug不至于暴死强测，但是因为在修改完bug之后已经深夜，就没有再测试多余的数据，强测错了一个点，第三次强测之前尝试用同学的评测机跑数据，但是始终得到的时fail的结果，我同第一次一样，仅仅手捏了几组数据就草草过了中测弱测，结果却忽略了一个基本的信息：求导因子的前导符号，强测又双叒叕挂了三个点。OO的三次作业让我深刻认识到了进行大量测试的重要性，在之后的作业里，一定要进行大量且可靠的测试

总之希望自己可以有所进步orzzzzzzzzz。