数据结构排序——计数排序和排序总结（附上912. 排序数组讲解）

本文主要是介绍数据结构排序——计数排序和排序总结（附上912. 排序数组讲解），希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

数据结构排序——计数排序和排序总结

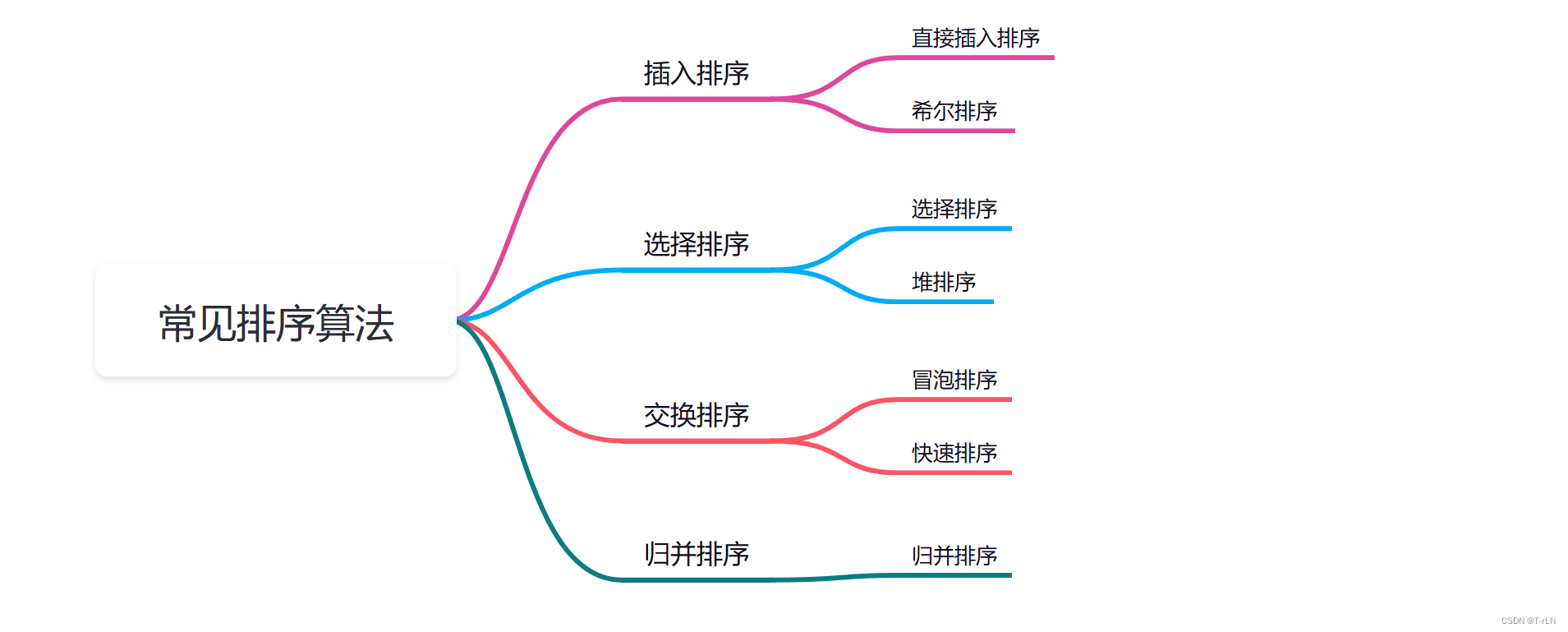
现在常见算法排序都已讲解完成，今天就再讲个计数排序。再总结一下

---

---

1.计数排序

计数排序是一种非基于比较的排序算法，它通过统计数组中每个元素出现的次数，然后根据元素的值和出现次数重新构造数组，从而实现排序。计数排序适用于元素范围比较小且元素非负的情况

步骤：

1. 找出待排序的数组中最大和最小的元素：min和max
2. 统计数组中每个值为 i 的元素出现的次数，存入新建数组 C 的第 i-min 项(c初始化时都是0)，每遇到一次，对应下标上的数就++
3. 反向填充目标数组：利用新建的数组把数据覆盖回去

时间复杂度：O(n + range)

void CountSort(int* a, int n)
{//先找最大最小，确定范围int max = a[0], min = a[0];for (int i = 1; i < n; i++){if (a[i] > max){max = a[i];}if (a[i] < min){min = a[i];}}int range = max - min + 1;int* count= (int*)calloc(sizeof(int) * range);if (count == NULL){perror("malloc fail");return;}//开始想count中累加了for (int i = 0; i < n; i++){count[a[i] - min]++;}//赋值覆盖int a_index = 0;for (int i = 0; i < range; i++){for (int j = 0; j < count[i]; j++){a[a_index] = i + min;a_index++;}}
}int main()
{int a[] = { 2,4,1,7,9 };CountSort(a, 5);for (int i = 0; i < 5; i++){printf("%d ", a[i]);}return 0;
}

2.排序总结

排序算法	时间复杂度	空间复杂度	稳定性
直接插入排序	O(N^2)	O(1)	稳定
希尔排序	O(N^1.3)	O(logN)	不稳定
选择排序	O(N^2)	O(N)	不稳定
堆排序	O(N*logN)	O(N)	不稳定
冒泡排序	O(N^2)	O(1)	稳定
快速排序	O(N*logN)	O(logN)	不稳定
归并排序	O(N*logN)	O(N)	稳定

不稳定的情况之一：

1. 希尔：根据gap分组不在一个组
2. 选择：3 3 1 1…
3. 堆排序：向下调整过程
4. 快排：相同的数字其中一个在keyi的位置

---

3.排序oj（排序数组）

题目详情

912. 排序数组 - 力扣（LeetCode）

代码

void Swap(int* x, int* y)
{int tmp = *x;*x = *y;*y = tmp;
}int GetMid(int* a,int left, int right)//找中间的
{// a[left]      a[mid]           a[right]int mid = left+(rand()%(right-left));if (a[left] < a[mid]){if (a[mid] < a[right]){return mid;}else if (a[left] > a[right])  // mid是最大值{return left;}else{return right;}}else // a[left] > a[mid]{if (a[left] < a[right]){return left;}else if (a[mid] < a[right]){return right;}else{return mid;}}
}void QuickSort(int* a, int left, int right)
{if (left >= right){return;}int begin = left;int end = right;int mid = GetMid(a, left, right);Swap(&a[mid], &a[left]);int cur = left + 1;int key = a[left];//储存一下，后面比较来用，用a[left]会被替代while (cur <= right){if (a[cur] < key){Swap(&a[cur], &a[left]);cur++;left++;}else if (a[cur] == key){cur++;}else{Swap(&a[cur], &a[right]);right--;}}QuickSort(a, begin, left - 1);QuickSort(a, right + 1, end);
}int* sortArray(int* nums, int numsSize, int* returnSize) {srand(time(0));QuickSort(nums,0,numsSize-1);*returnSize=numsSize;return nums;
}

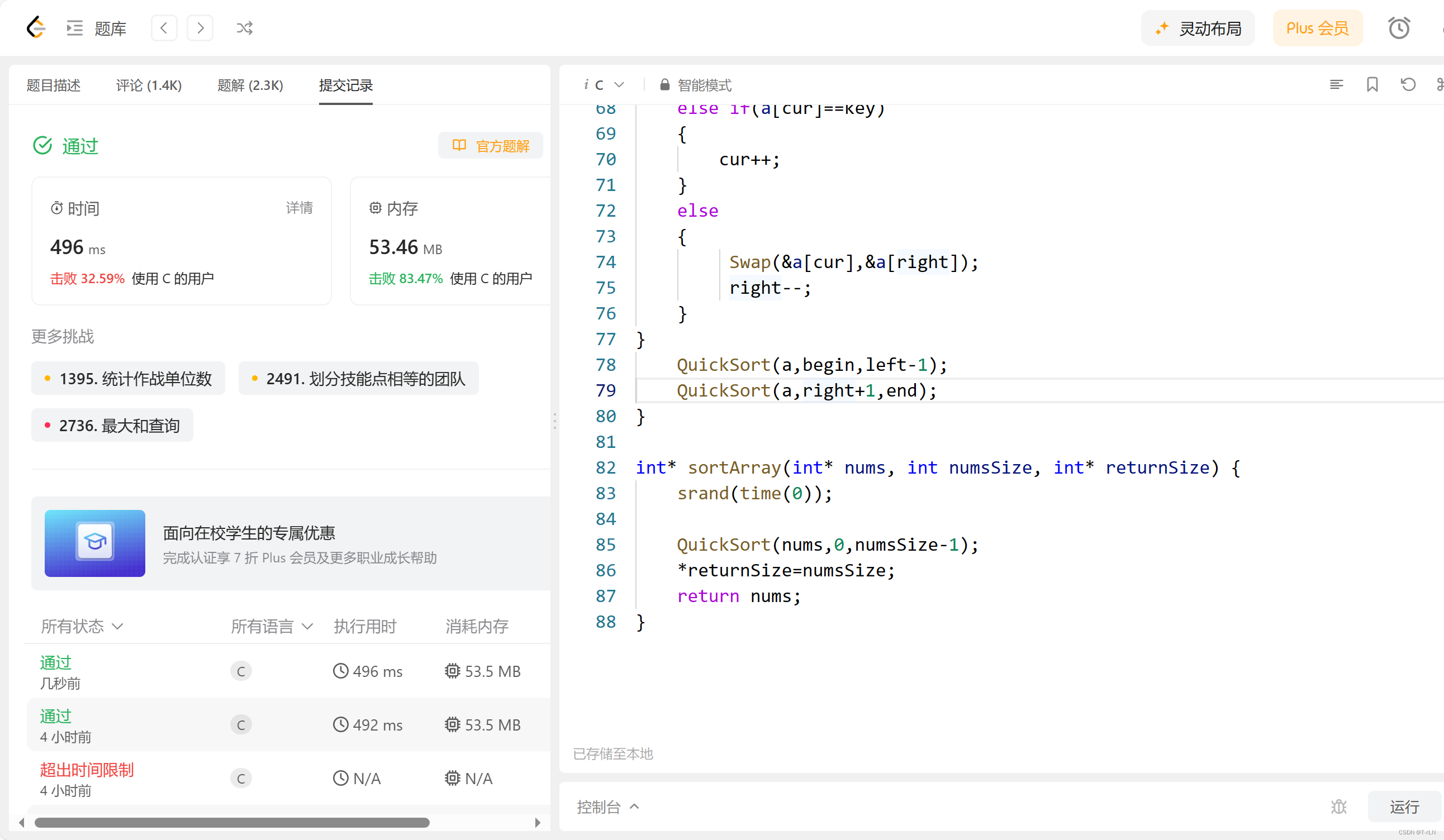
1. Swap函数： 这是一个用于交换两个整数值的简单函数。
2. GetMid函数： 用于在数组中找到三个位置（左、中、右）的元素，从而选取合适的中间值。它通过比较这三个位置的元素，找到其中介于最小和最大之间的值。
3. QuickSort函数：实现了快速排序的核心逻辑
   • 选择中间值，并将其与数组的第一个元素交换，作为基准值。
   • 遍历数组，将小于基准值的元素移到基准值左侧，大于基准值的元素移到右侧，相等的元素留在中间。
   • 对基准值左右两侧的子数组递归地进行快速排序，直到左右两侧都排好序

思路

这题有根据快排的痛点进行特地进行测试用例的编写

一开始大家肯定就直接放上去一个快排，结果发现：超时了（过不去的测试用例是有序的）

• 所以第一次我们要加上三选一
• 发现还不行（过不去的是数字全部一样），现在就考虑换上三路划分
• 最后发现测试用例可以，但是时间过长，就改一下Getmid函数，之前mid是$(left+right)/2$,现在是left+(rand()%(right-left))

好啦，排序的内容也到这里啦。下面就要开启c++的内容了

这篇关于数据结构排序——计数排序和排序总结（附上912. 排序数组讲解）的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---