每日算法打卡：蚂蚁感冒 day 13

本文主要是介绍每日算法打卡：蚂蚁感冒 day 13，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

原题链接

1211. 蚂蚁感冒

题目难度：简单

题目来源：第五届蓝桥杯省赛C++ A/B组

题目描述

长 100 厘米的细长直杆子上有 n 只蚂蚁。

它们的头有的朝左，有的朝右。

每只蚂蚁都只能沿着杆子向前爬，速度是 1 厘米/秒。

当两只蚂蚁碰面时，它们会同时掉头往相反的方向爬行。

这些蚂蚁中，有 1 只蚂蚁感冒了。

并且在和其它蚂蚁碰面时，会把感冒传染给碰到的蚂蚁。

请你计算，当所有蚂蚁都爬离杆子时，有多少只蚂蚁患上了感冒。

输入格式

第一行输入一个整数 n, 表示蚂蚁的总数。

接着的一行是 n 个用空格分开的整数 $X_i$, $X_i$ 的绝对值表示蚂蚁离开杆子左边端点的距离。

正值表示头朝右，负值表示头朝左，数据中不会出现 0 值，也不会出现两只蚂蚁占用同一位置。

其中，第一个数据代表的蚂蚁感冒了。

输出格式

输出1个整数，表示最后感冒蚂蚁的数目。

数据范围

$1<n<50$,
$0<|X_i|<100$

输入样例1：

3
5 -2 8 

输出样例1：

1 

输入样例2：

5
-10 8 -20 12 25 

输出样例2：

3 

题目分析

这道题其实就是一个脑筋急转弯，当两只蚂蚁相遇时就会掉头，有一只蚂蚁感冒，在相遇是会传染，从而不断传播，问当所有蚂蚁走出杆子时，有多少只蚂蚁感冒了

首先需要确定的是，所有的蚂蚁是否会离开这个杆子，其次需要确定的是，如何求被感染的蚂蚁的个数

这里其实是有一个等效的思想，假设两只蚂蚁相遇，那么他们会互相掉头，其实就等效他们互相穿过，只是状态不一样，那么对于状态我们也可以分类，两个都没有感冒，则穿过后都不感冒，只要有一个感冒，那么穿过后都感冒

此时问题就简单多了，我们画一个示意图

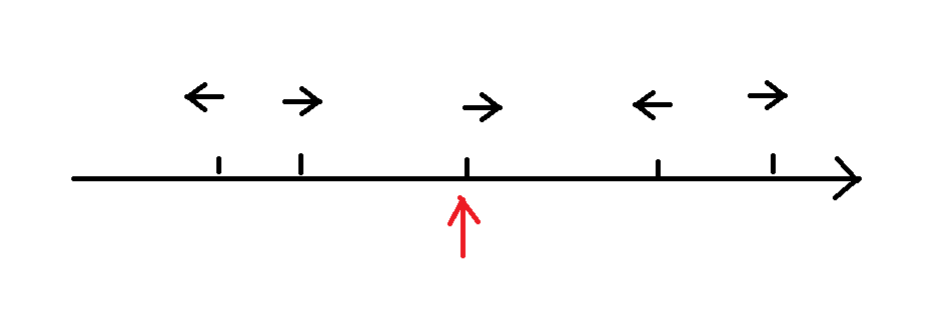
假设中间的这个蚂蚁感冒了，那么我们就可以知道，在他左边向左走的和在他右边向右走的蚂蚁必定不会感冒，在他右边向左走的蚂蚁必定感冒

在左边向右的蚂蚁就需要分情况讨论了，如果右边有向左走的蚂蚁，那么左边有向右走的蚂蚁都会被感染，如果右边没有，那么左边也都不会被感染，最终就只有最初的蚂蚁

当然这里是只挑选的初始的蚂蚁是向右的情况，如果初始蚂蚁向左就是相反的了

示例代码

#include<iostream>
#include<cmath>
using namespace std;const int N = 55;int n;
int arr[N];int main()
{cin>>n;int left = 0, right = 0; // 表示左边向右走的蚂蚁数量，右边向左走的蚂蚁数量for(int i=0;i<n;i++){cin>>arr[i];}for(int i=1;i<n;i++){if(abs(arr[i])<abs(arr[0])&&arr[i]>0) // 在左边且向右走left++;else if(abs(arr[i])>abs(arr[0])&&arr[i]<0) // 在右边向左走right++;}if((arr[0]>0&&right==0)||(arr[0]<0&&left==0))cout<<1<<'\n';elsecout<<left+right+1<<'\n';return 0;
}

这篇关于每日算法打卡：蚂蚁感冒 day 13的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---