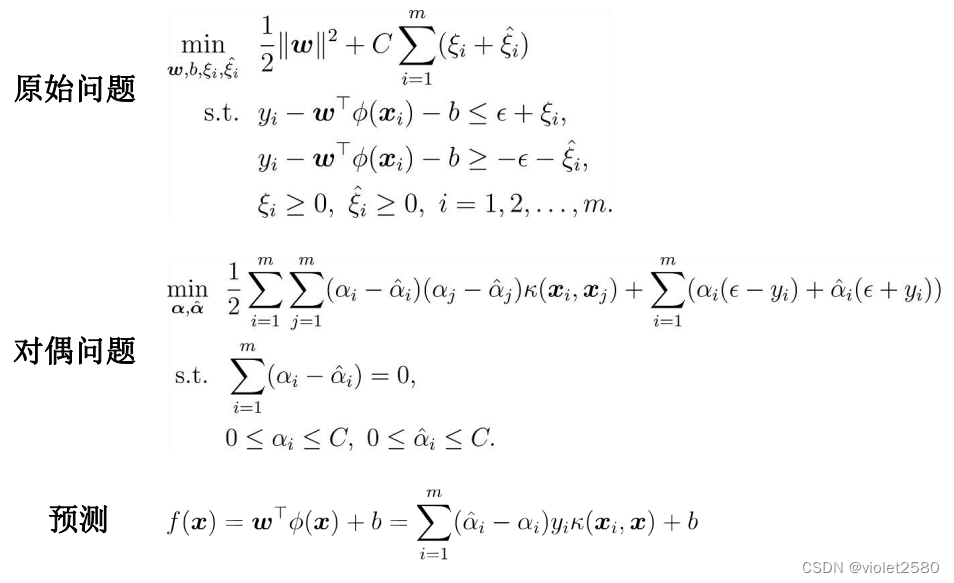机器学习实验课7 支持向量机（SVM）

本文主要是介绍机器学习实验课7 支持向量机（SVM），希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

前言：支持向量机（support vector machines, SVM）是一种二分类模型，它的基本模型是定义在特征空间上的间隔最大的线性分类器，间隔最大使它有别于感知机；SVM还包括核技巧，这使它成为实质上的非线性分类器。SVM的的学习策略就是间隔最大化，可形式化为一个求解凸二次规划的问题，也等价于正则化的合页损失函数的最小化问题。SVM的的学习算法就是求解凸二次规划的最优化算法。

一、SVM原理

1.间隔与支持向量

1.1线性可分

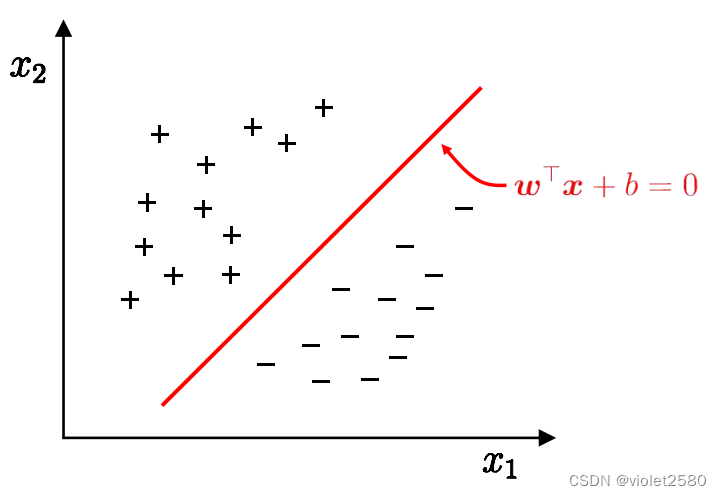
在二维空间上，两类点被一条直线完全分开叫做线性可分。

为了使这个超平面更具鲁棒性，我们会去找最佳超平面，以最大间隔把两类样本分开的超平面，也称之为最大间隔超平面。应选择”正中间” , 容忍性好, 鲁棒性高, 泛化能力最强，如下图所示，应选择红线。

1.2支持向量

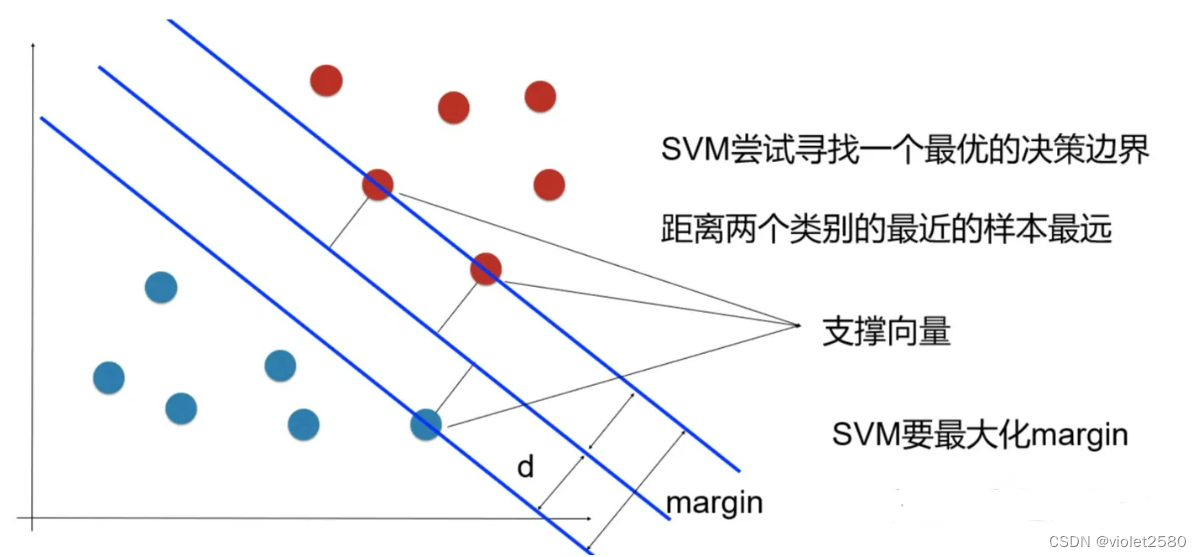
样本中距离超平面最近的一些点，这些点叫做支持向量。

1.3SVM最优化

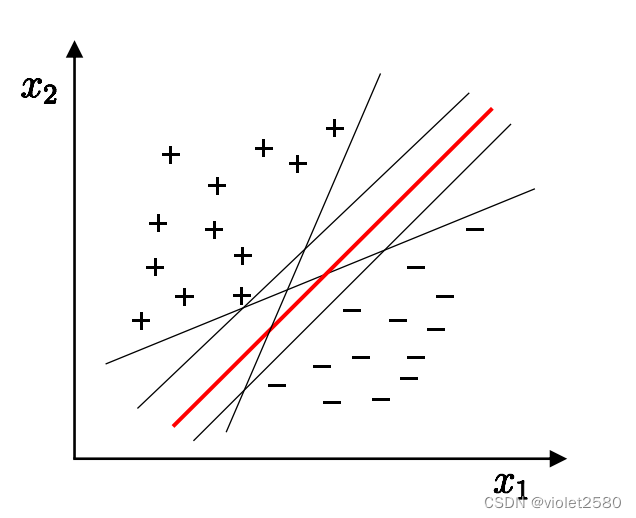
SVM 想要的就是找到各类样本点到超平面的距离最远，也就是找到最大间隔超平面。任意超平面可以用下面这个线性方程来描述：

$w^Tx+b=0 \\$

二维空间点 (x,y) 到直线 Ax+By+C=0 的距离公式是：

$\frac{|Ax+By+C|}{\sqrt{A^2+B^2}} \\$

扩展到 n 维空间后，点 x=(x_1,x_2…x_n) 到直线 $w^Tx+b=0$ 的距离为：

$\frac{|w^Tx+b|}{||w||} \\$

其中

如图所示，根据支持向量的定义我们知道，支持向量到超平面的距离为 d，其他点到超平面的距离大于 d。

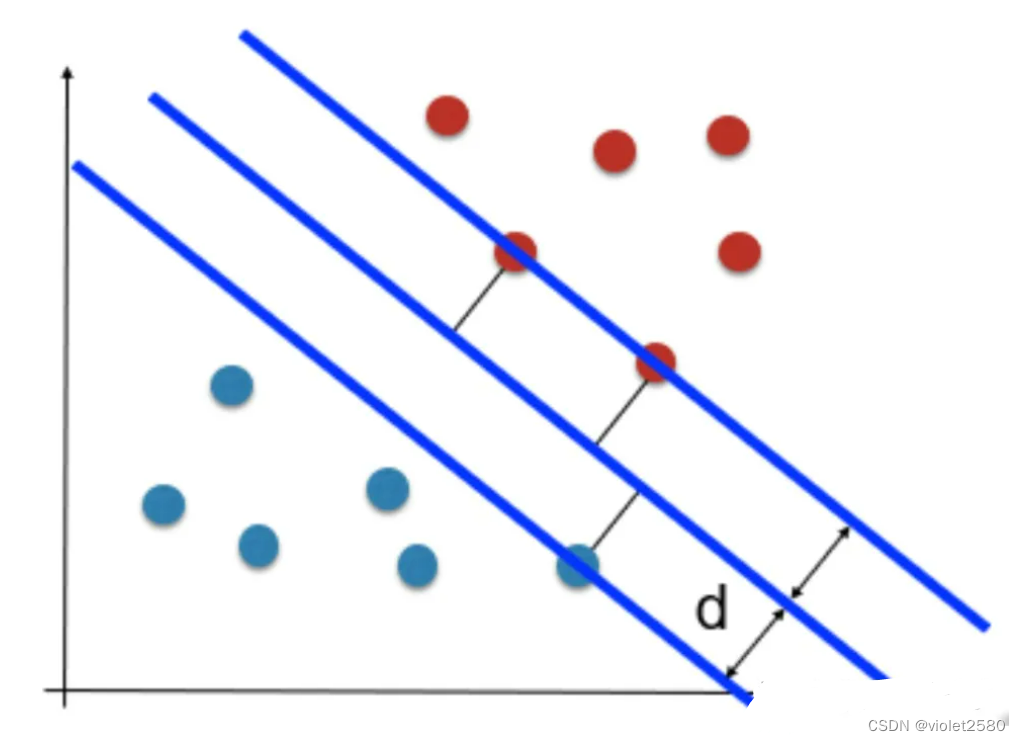
于是我们有这样的一个公式：

$\left\{ \begin{aligned} \frac{w^Tx+b}{||w||} &\geq d \quad y=1 \\ \frac{w^Tx+b}{||w||} &\leq -d \quad y=-1 \end{aligned} \right. \\$

稍作转化可以得到：

$\left\{ \begin{aligned} \frac{w^Tx+b}{||w||d} &\geq 1 \quad y=1 \\ \frac{w^Tx+b}{||w||d} &\leq -1 \quad y=-1 \end{aligned} \right. \\$

||w|| d 是正数，我们暂且令它为 1（之所以令它等于 1，是为了方便推导和优化，且这样做对目标函数的优化没有影响），故：

$\left\{ \begin{aligned} w^Tx+b &\geq 1 \quad y=1 \\ w^Tx+b &\leq -1 \quad y=-1 \end{aligned} \right. \\$

将两个方程合并，我们可以简写为：

$y(w^Tx+b) \geq 1 \\$

至此我们就可以得到最大间隔超平面的上下两个超平面：

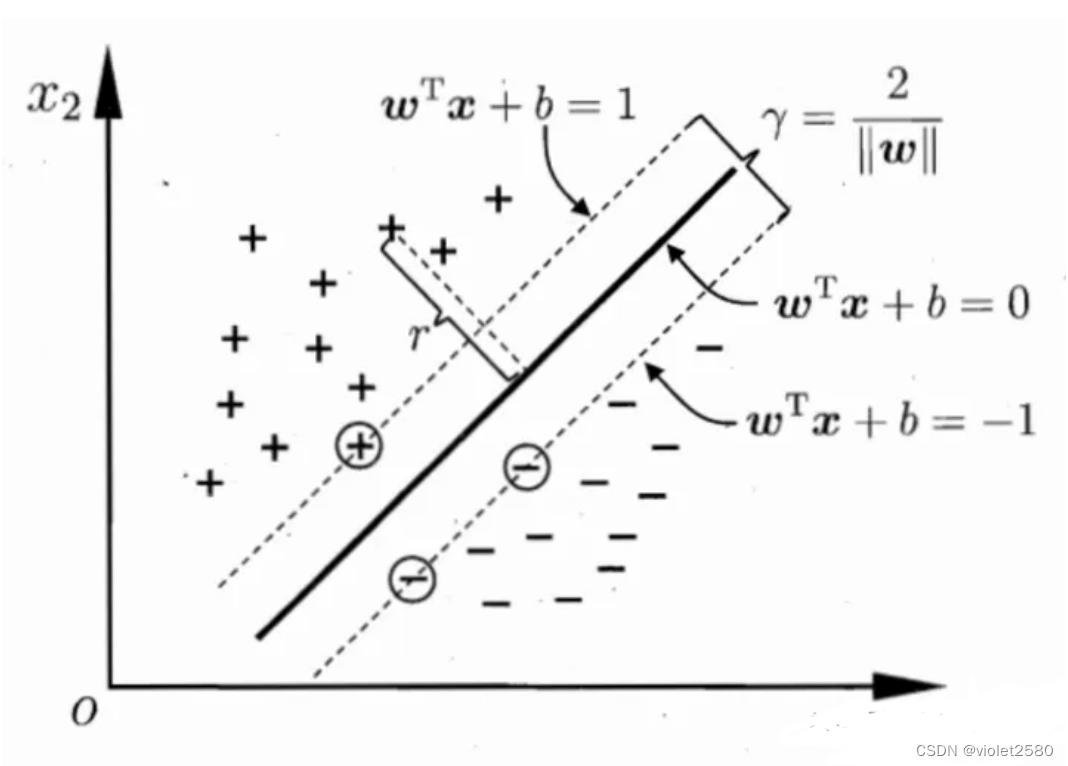
每个支持向量到超平面的距离可以写为：

$d=\frac{|w^Tx+b|}{||w||} \\$

由上述 y(w^Tx+b) > 1 > 0 可以得到 y(w^Tx+b) = |w^Tx+b| ，所以我们得到：

$d = \frac{y(w^Tx+b)}{||w||} \\$

最大化这个距离：

$\max 2* \frac{y(w^Tx+b)}{||w||} \\$

这里乘上 2 倍也是为了后面推导，对目标函数没有影响。刚刚我们得到支持向量 y(w^Tx+b) = 1 ，所以我们得到：

$\max \frac{2}{||w||} \\$

再做一个转换：

$\min \frac{1}{2}||w|| \\$

为了方便计算（去除 ||w|| 的根号），我们有：

$\min \frac{1}{2}||w||^2\\$

所以得到的最优化问题是：

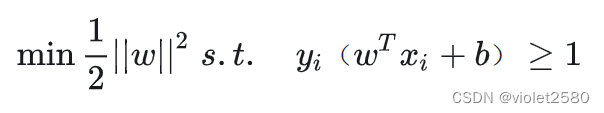
2.对偶问题

2.1拉格朗日乘数法

拉格朗日乘数法是等式约束优化问题：

$\min f(x_{1} ,x_{2} ,...,x_{n} ) \\ s.t. \quad h_{k} (x_{1} ,x_{2} ,...,x_{n} )=0 \quad k =1,2,...,l\\$

我们令 $L(x,\lambda ) = f(x) + \sum\limits_{k = 1}^l \lambda _k h_k (x)$ ，函数 L(x,y) 称为 Lagrange 函数，参数 \lambda 称为 Lagrange 乘子没有非负要求。

利用必要条件找到可能的极值点：

$\left\{ \begin{aligned} \frac{\partial L}{\partial x_i} = 0 \quad i=1,2,...,n \\ \frac{\partial L}{\partial \lambda_k} = 0 \quad k=1,2,...,l \end{aligned} \right. \\$

具体是否为极值点需根据问题本身的具体情况检验。这个方程组称为等式约束的极值必要条件。

等式约束下的 Lagrange 乘数法引入了 l 个 Lagrange 乘子，我们将 $x_{i}$ 与 $\lambda_{k}$ 一视同仁，把 $\lambda_{k}$ 也看作优化变量，共有 (n+l) 个优化变量。

2.2 不等式约束优化问题

而我们现在面对的是不等式优化问题，针对这种情况其主要思想是将不等式约束条件转变为等式约束条件，引入松弛变量，将松弛变量也是为优化变量。

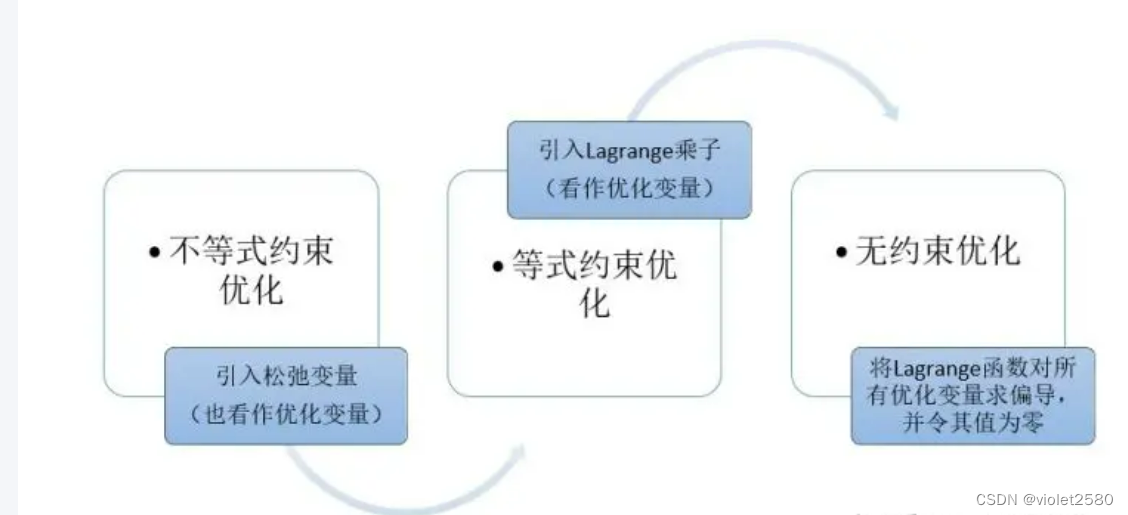
以我们的例子为例：

$min f(w) = min\frac{1}{2} ||w||^2 \\ s.t. \quad g_i(w) = 1 - y_i(w^Tx_i+b)\leq 0 \\$

我们引入松弛变量 $a_i^2$ 得到 $h_i(w,a_i) = g_i(w) + a_i^2 = 0$ 。这里加平方主要为了不再引入新的约束条件，如果只引入 $a_i$ 那我们必须要保证 $a_i \geq 0$ 才能保证 $h_i(w,a_i) = 0$ ，这不符合我们的意愿。

由此我们将不等式约束转化为了等式约束，并得到 Lagrange 函数：

$\begin{aligned} L(w,\lambda,a) &= {f(w)} + \sum\limits_{i = 1}^n \lambda_i h_i (w) \\ &= {f(w)} + \sum\limits_{i = 1}^n \lambda_i [g_i(w) + a_i^2] \quad \lambda_i \geq 0 \end{aligned} \\$

由等式约束优化问题极值的必要条件对其求解，联立方程：

$\left\{ \begin{aligned} \frac{\partial L}{\partial w_i} &= \frac{\partial f}{\partial w_i} + \sum\limits_{i=1}^{n} \lambda_i \frac{\partial g_i}{\partial w_i}= 0, \\ \frac{\partial L}{\partial a_i} &= 2 \lambda_i a_i = 0, \\ \frac{\partial L}{\partial \lambda_i} &= g_i(w) + a_i^2 = 0, \\ \lambda_i &\geq 0 \end{aligned} \right. \\$

（为什么取 $\lambda_i \geq 0$ ，可以通过几何性质来解释，有兴趣的同学可以查下 KKT 的证明）。

针对 $\lambda_i a_i$ = 0 我们有两种情况：

情形一： $\lambda_i = 0, a_i \neq 0$

由于 $\lambda_i=0$ ，因此约束条件 $g_i(w)$ 不起作用，且 $g_i(w)<0$

情形二： $\lambda_i \neq 0, a_i = 0$

此时 $g_i(w)=0$ 且 $\lambda_i>0$ ，可以理解为约束条件 $g_i(w)$ 起作用了，且 $g_i(w)=0$

综合可得： $\lambda_ig_i(w)=0$ ，且在约束条件起作用时 $\lambda_i>0,g_i(w)=0$ ；约束不起作用时 $\lambda_i = 0,g_i(w) < 0$

由此方程组转换为：

$\left\{ \begin{aligned} \frac{\partial L}{\partial w_i} &= \frac{\partial f}{\partial w_i} + \sum\limits_{j=1}^{n} \lambda_j \frac{\partial g_j}{\partial w_i}= 0, \\ \lambda_ig_i(w) &= 0, \\ g_i(w)&\leq 0 \\ \lambda_i &\geq 0 \end{aligned} \right. \\$

以上便是不等式约束优化优化问题的 KKT(Karush-Kuhn-Tucker) 条件， \lambda_i 称为 KKT 乘子。

这个式子告诉了我们什么事情呢？

直观来讲就是，支持向量 $g_i(w)=0$ ，所以 $\lambda_i > 0$ 即可。而其他向量 $g_i(w)<0, \lambda_i=0$ 。

我们原本问题时要求： $min \frac{1}{2} ||w||^2$ ，即求 $minL(w,\lambda,a)$

$\begin{aligned} L(w,\lambda,a) &= {f(w)} + \sum\limits_{i = 1}^n \lambda_i [g_i(w) + a_i^2] \quad \\ &= {f(w)} + \sum\limits_{i = 1}^n \lambda_i g_i(w) + \sum\limits_{i = 1}^n \lambda_i a_i^2 \end{aligned} \\$

由于 $\sum\limits_{i = 1}^n \lambda_i a_i^2 \geq 0$ ，故我们将问题转换为： $minL(w,\lambda)$ ：

$L(w,\lambda)={f(w)} + \sum\limits_{i = 1}^n \lambda_i g_i(w) \\$

假设找到了最佳参数是的目标函数取得了最小值 p。即 $\frac{1}{2} ||w||^2 =p$ 。而根据 $\lambda_{i} \geq 0$ ，可知 $\sum\limits_{i = 1}^n \lambda_i g_i(w) \leq 0$ ，因此 $L(w,\lambda) \leq p$ ，为了找到最优的参数 ${\lambda}$ ，使得 $L(w,\lambda)$ 接近 p，故问题转换为出 $\max\limits_{\lambda}L(w,\lambda)$ 。

故我们的最优化问题转换为：

$\min\limits_w \max\limits_{\lambda} L(w,\lambda) \\ s.t. \quad \lambda_i \geq 0 \\$

出了上面的理解方式，我们还可以有另一种理解方式：由于 $\lambda_i \geq 0$ ，

$\max\limits_{\lambda} L(w, \lambda) = \left\{ \begin{aligned} \infty \quad g_i(w) \geq 0 \\ \frac{1}{2} {||w||^2} \quad g_i(w) \leq 0 \end{aligned} \right. \\$

所以 $\min(\infty, \frac{1}{2} {||w||^2}) = \frac{1}{2} {||w||^2}$ ，所以转化后的式子和原来的式子也是一样的。

2.2 强对偶性

对偶问题其实就是将：

$\min\limits_w \max\limits_{\lambda} L(w,\lambda) \\ s.t. \quad \lambda_i \geq 0 \\$

变成了：

$\max\limits_{\lambda} \min\limits_w L(w,\lambda) \\ s.t. \quad \lambda_i \geq 0 \\$

假设有个函数 f 我们有：

$\min\max f \geq \max\min f \\$

也就是说，最大的里面挑出来的最小的也要比最小的里面挑出来的最大的要大。这关系实际上就是弱对偶关系，而强对偶关系是当等号成立时，即：

$\min\max f = \max\min f \\$

如果 f 是凸优化问题，强对偶性成立。而我们之前求的 KKT 条件是强对偶性的充要条件。

2.3.SVM 优化

我们已知 SVM 优化的主问题是：

$\min\limits_{w} \frac{1}{2} ||w||^2 \\$ $s.t.\quad$

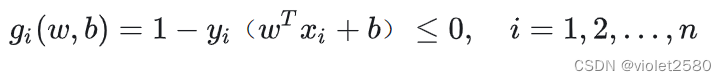
那么求解线性可分的 SVM 的步骤为：

步骤 1：

构造拉格朗日函数：

$\min\limits_{w,b}\max\limits_{\lambda} L(w,b,\lambda)= \frac{1}{2}{||w||}^2 + \sum\limits_{i = 1}^n \lambda_i [1-y_i(w^Tx_i+b)] \\ s.t. \quad \lambda_i \geq 0 \\$

步骤 2：

利用强对偶性转化：

$\max\limits_{\lambda}\min\limits_{w,b} L(w,b,\lambda) \\$

现对参数 w 和 b 求偏导数：

$\begin{aligned} \frac{\partial L}{\partial w} &= w - \sum_{i=1}^{n}\lambda_ix_iy_i = 0 \\ \frac{\partial L}{\partial b} &= \sum_{i=1}^{n}\lambda_iy_i = 0 \\ \end{aligned} \\$

得到：

$\begin{aligned} \sum_{i=1}^{n}\lambda_ix_iy_i &= w\\ \sum_{i=1}^{n}\lambda_iy_i &= 0 \\ \end{aligned} \\$

我们将这个结果带回到函数中可得：

$\begin{aligned} L(w,b,\lambda) &= \frac{1}{2}\sum_{i=1}^{n}\sum_{j=1}^{n}\lambda_i \lambda_j y_i y_j (x_i \cdot x_j) + \sum_{i = 1}^n \lambda_i - \sum_{i = 1}^n \lambda_i y_i(\sum_{j = 1}^n \lambda_j y_j (x_i \cdot x_j) + b) \\ &= \frac{1}{2}\sum_{i=1}^{n}\sum_{j=1}^{n}\lambda_i \lambda_j y_i y_j (x_i \cdot x_j) + \sum_{i = 1}^n \lambda_i - \sum_{i=1}^{n}\sum_{j=1}^{n}\lambda_i \lambda_j y_i y_j (x_i \cdot x_j)-\sum_{i = 1}^n \lambda_i y_i b \\ &= \sum_{j=1}^{n}\lambda_i-\frac{1}{2}\sum_{i=1}^{n}\sum_{j=1}^{n}\lambda_i \lambda_j y_i y_j (x_i \cdot x_j) \end{aligned} \\$

也就是说：

$\min\limits_{w,b}L(w,b,\lambda) = \sum_{j=1}^{n}\lambda_i-\frac{1}{2}\sum_{i=1}^{n}\sum_{j=1}^{n}\lambda_i \lambda_j y_i y_j (x_i \cdot x_j) \\$

步骤 3：

由步骤 2 得：

$\max\limits_{\lambda} [\sum_{j=1}^{n}\lambda_i-\frac{1}{2}\sum_{i=1}^{n}\sum_{j=1}^{n}\lambda_i \lambda_j y_i y_j (x_i \cdot x_j)] \\ s.t. \quad \sum_{i=1}^{n}\lambda_iy_i = 0 \quad \lambda_i \geq 0 \\$

我们可以看出来这是一个二次规划问题，问题规模正比于训练样本数，我们常用 SMO(Sequential Minimal Optimization) 算法求解。

SMO(Sequential Minimal Optimization)，序列最小优化算法，其核心思想非常简单：每次只优化一个参数，其他参数先固定住，仅求当前这个优化参数的极值。我们来看一下 SMO 算法在 SVM 中的应用。

我们刚说了 SMO 算法每次只优化一个参数，但我们的优化目标有约束条件： $\sum\limits_{i=1}^{n}\lambda_iy_i = 0$ ，没法一次只变动一个参数。所以我们选择了一次选择两个参数。具体步骤为：

选择两个需要更新的参数 $\lambda_i$ 和 $\lambda_j$ ，固定其他参数。于是我们有以下约束：

这样约束就变成了：

$\lambda_i y_i+\lambda_j y_j = c \quad \lambda_i \geq 0,\lambda_j \geq 0 \\$

其中 $c=-\sum\limits_{k \ne i,j}\lambda_ky_k$ ，由此可以得出 $\lambda_j=\frac{c-\lambda_iy_i}{y_j}$ ，也就是说我们可以用 \lambda_i 的表达式代替 $\lambda_{j}$ 。这样就相当于把目标问题转化成了仅有一个约束条件的最优化问题，仅有的约束是 $\lambda_i \geq 0$ 。

2. 对于仅有一个约束条件的最优化问题，我们完全可以在 $\lambda_{i}$ 上对优化目标求偏导，令导数为零，从而求出变量值 $\lambda_{i_{new}}$ ，然后根据 $\lambda_{i_{new}}$ 求出 $\lambda_{j_{new}}$ 。

3. 多次迭代直至收敛。

通过 SMO 求得最优解 $\lambda^*$ 。

步骤 4 ：

我们求偏导数时得到：

$w = \sum_{i=1}^m \lambda_i y_i x_i \\$

由上式可求得 w。

我们知道所有 $\lambda_i > 0$ 对应的点都是支持向量，我们可以随便找个支持向量，然后带入： $y_s(wx_s+b) = 1$ ，求出 b 即可，

两边同乘 $y_s$ ，得 $y_s^2(wx_s+b) = y_s$

因为 $y_s^2=1$ ，所以： $b=y_s - wx_s$

为了更具鲁棒性，我们可以求得支持向量的均值：

$b = \frac{1}{|S|}\sum_{s \in S} (y_s -wx_s) \\$

步骤 5： w 和 b 都求出来了，我们就能构造出最大分割超平面： w^Tx+b=0

分类决策函数： $f(x)=sign(w^Tx+b)$

其中 $sign( \cdot )$ 为阶跃函数：

$sign(x) = \left\{ \begin{aligned} -1 \quad x<0 \\ 0 \quad x=0 \\ 1 \quad x>0 \end{aligned} \right. \\$

将新样本点导入到决策函数中既可得到样本的分类。

3.软间隔与正则化

3.1 解决问题

在实际应用中，完全线性可分的样本是很少的，如果遇到了不能够完全线性可分的样本，我们应该怎么办？比如下面这个：

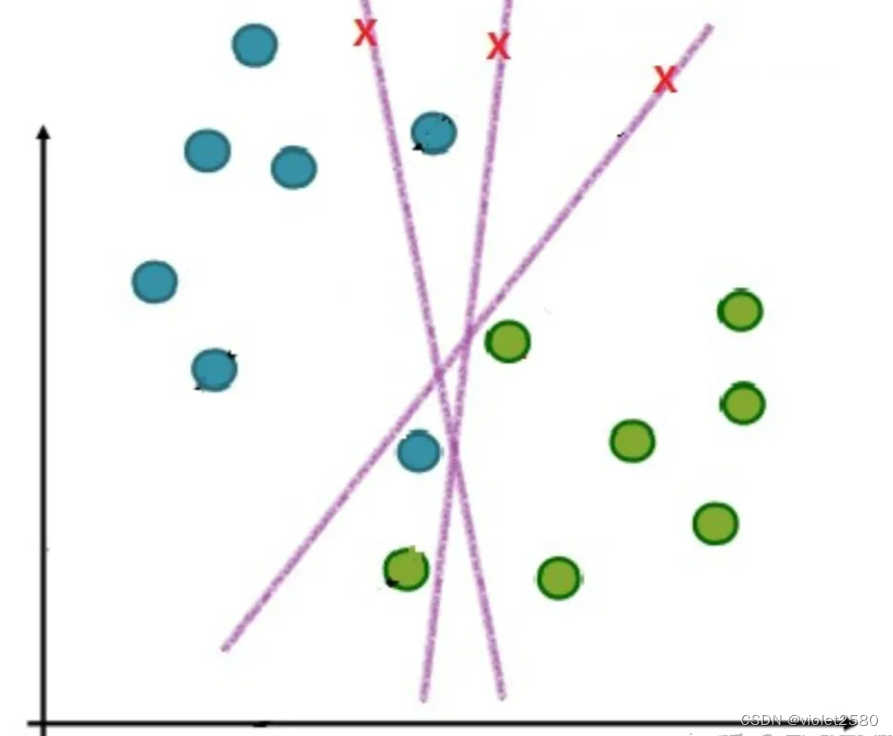
于是我们就有了软间隔，相比于硬间隔的苛刻条件，我们允许个别样本点出现在间隔带里面，比如：

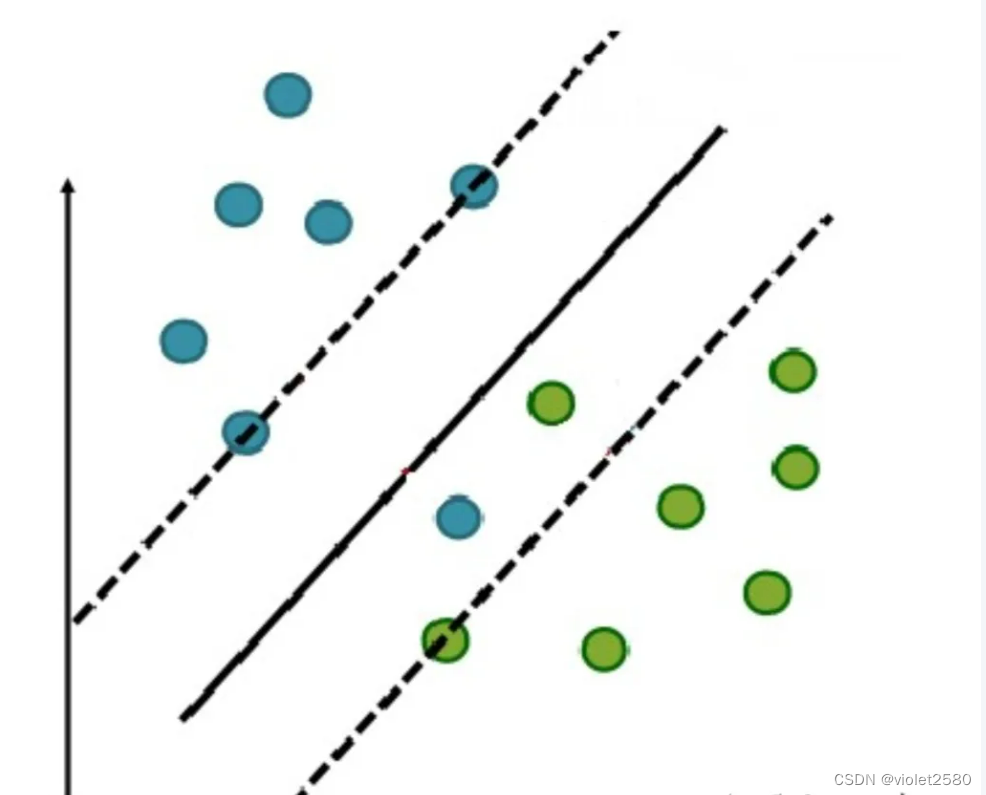
我们允许部分样本点不满足约束条件：

$1-y_i(w^Tx_i + b) \leq 0 \\$

为了度量这个间隔软到何种程度，我们为每个样本引入一个松弛变量 $\xi_{i}$ ，令 $\xi_{i} \geq 0$ ，且 $1 - y_i(w^Tx_i + b)-\xi_i \leq 0$ 。对应如下图所示：

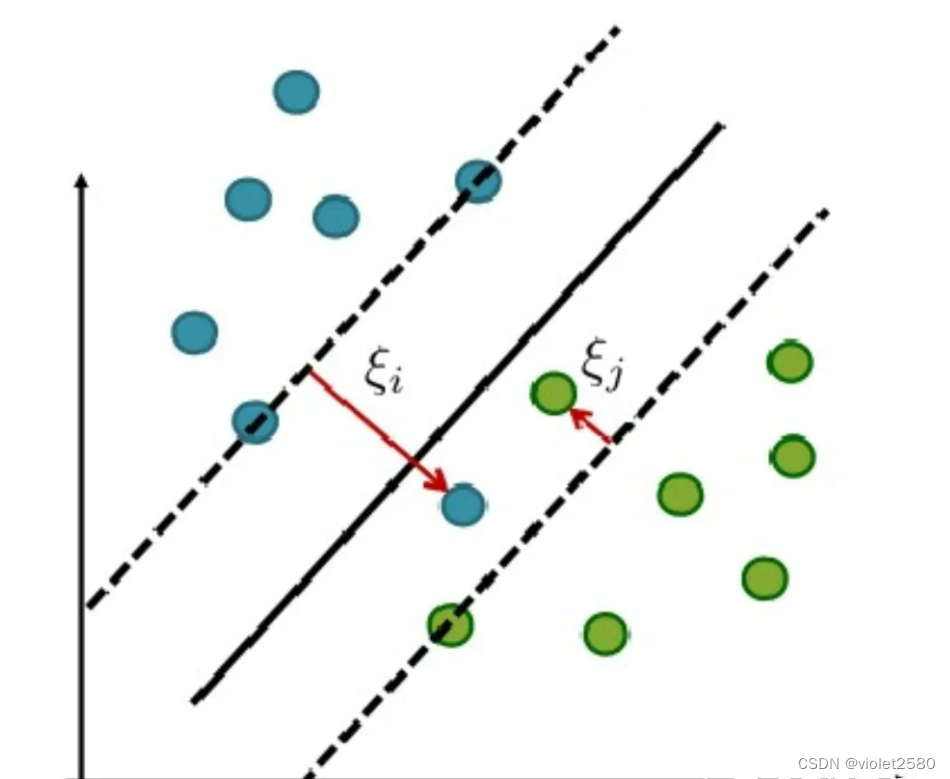
3.2 优化目标及求解

增加软间隔后我们的优化目标变成了：

$\min\limits_{w} \frac{1}{2} ||w||^2 + C\sum_{i=1}^{m}\xi_i \\ s.t.\quad g_i(w,b) = 1 - y_i(w^Tx_i+b) - \xi_i\leq 0, \quad \xi_i \geq 0, \quad i=1,2,...,n \\$

其中 C 是一个大于 0 的常数，可以理解为错误样本的惩罚程度，若 C 为无穷大， \xi_{i} 必然无穷小，如此一来线性 SVM 就又变成了线性可分 SVM；当 C 为有限值的时候，才会允许部分样本不遵循约束条件。

接下来我们将针对新的优化目标求解最优化问题：

步骤 1：

构造拉格朗日函数：

$\min\limits_{w,b,\xi}\max\limits_{\lambda, \mu} L(w,b,\xi,\lambda,\mu)= \frac{1}{2}{||w||}^2 + C\sum_{i=1}^{m}\xi_i+ \sum\limits_{i = 1}^n \lambda_i [1-\xi_i-y_i(w^Tx_i+b)] - \sum_{i=1}^{n}\mu_i\xi_i \\ s.t. \quad \lambda_i \geq 0 \quad \mu_i \geq 0 \\$

其中 \lambda_{i} 和 \mu_{i} 是拉格朗日乘子，w、b 和 \xi_{i} 是主问题参数。

根据强对偶性，将对偶问题转换为：

$\max\limits_{\lambda, \mu}\min\limits_{w,b,\xi} L(w,b,\xi,\lambda,\mu) \\$

步骤 2：

分别对主问题参数w、b 和 \xi_{i} 求偏导数，并令偏导数为 0，得出如下关系：

$w = \sum_{i=1}^{m}\lambda_i y_i x_i \\ 0 = \sum_{i=1}^{m}\lambda_i y_i \\ C = \lambda_i + \mu_i \\$

将这些关系带入拉格朗日函数中，得到：

$\min\limits_{w,b,\xi}L(w,b,\xi,\lambda,\mu) = \sum_{j=1}^{n}\lambda_i-\frac{1}{2}\sum_{i=1}^{n}\sum_{j=1}^{n}\lambda_i \lambda_j y_i y_j (x_i \cdot x_j) \\$

最小化结果只有 $\lambda$ 而没有 $\mu$ ，所以现在只需要最大化 $\lambda$ 就好：

我们可以看到这个和硬间隔的一样，只是多了个约束条件。

然后我们利用 SMO 算法求解得到拉格朗日乘子 $\lambda^{*}$ 。

步骤 3 ：

$w = \sum_{i=1}^m \lambda_i y_i x_i \\ b = \frac{1}{|S|}\sum_{s \in S} (y_s -wx_s) \\$

然后我们通过上面两个式子求出 w 和 b，最终求得超平面 w^Tx+b=0 ，

这边要注意一个问题，在间隔内的那部分样本点是不是支持向量？

我们可以由求参数 w 的那个式子可看出，只要 $\lambda_{i} > 0$ 的点都能够影响我们的超平面，因此都是支持向量。

4.核函数

4.1 线性不可分

我们刚刚讨论的硬间隔和软间隔都是在说样本的完全线性可分或者大部分样本点的线性可分。

但我们可能会碰到的一种情况是样本点不是线性可分的，比如：

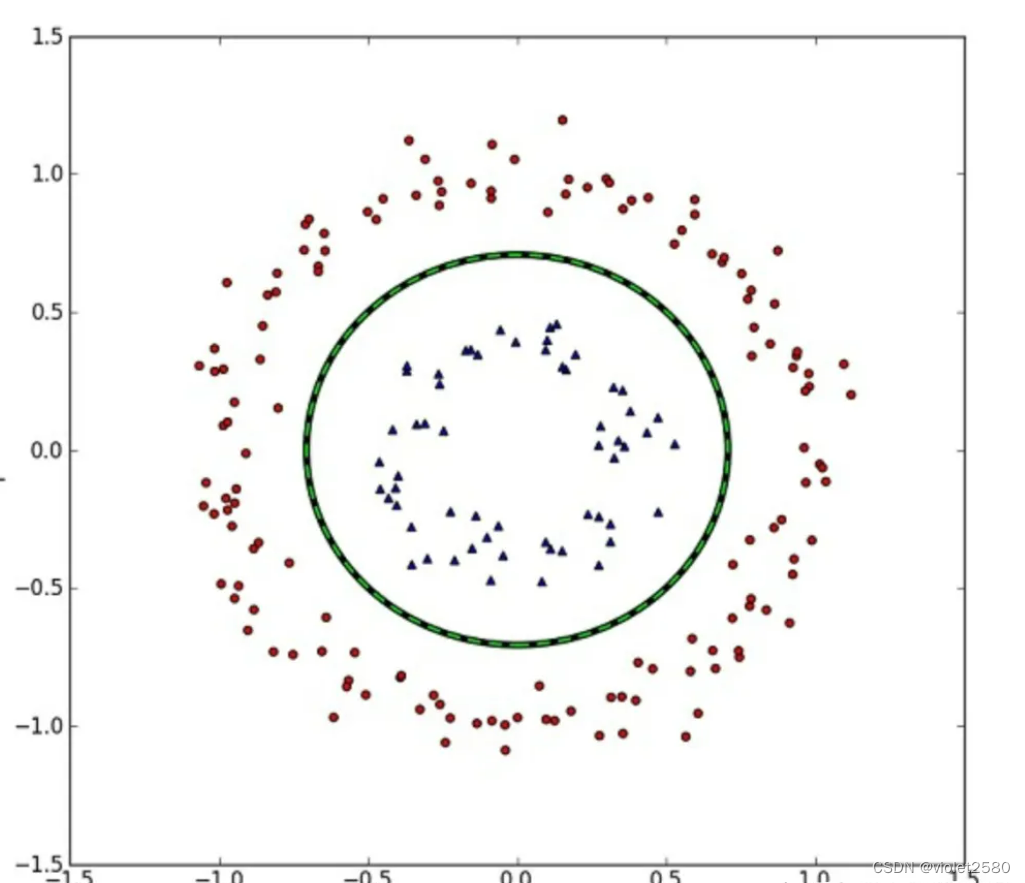
这种情况的解决方法就是：将二维线性不可分样本映射到高维空间中，让样本点在高维空间线性可分，比如：

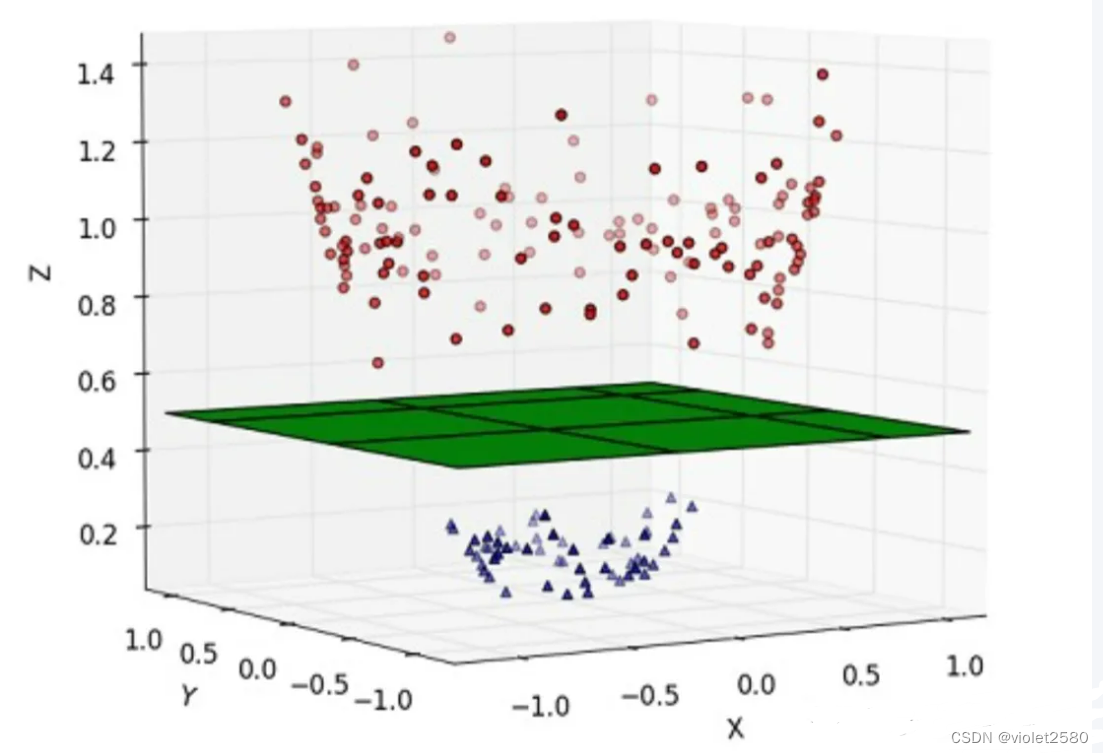
对于在有限维度向量空间中线性不可分的样本，我们将其映射到更高维度的向量空间里，再通过间隔最大化的方式，学习得到支持向量机，就是非线性 SVM。

我们用 x 表示原来的样本点，用 $\phi(x)$ 表示 x 映射到特征新的特征空间后到新向量。那么分割超平面可以表示为： $f(x)=w \phi(x)+b$ 。

对于非线性 SVM 的对偶问题就变成了：

$\min\limits_{\lambda} [\frac{1}{2}\sum_{i=1}^{n}\sum_{j=1}^{n}\lambda_i \lambda_j y_i y_j (\phi(x_i) \cdot \phi(x_j))-\sum_{j=1}^{n}\lambda_i] \\ s.t. \quad \sum_{i=1}^{n}\lambda_iy_i = 0, \quad \lambda_i \geq 0, \quad C-\lambda_i-\mu_i=0 \\$ $\sum_{i=1}^nx_i^2y_i^2+\sum_{i=2}^n\sum_{j=1}^{i-1}(\sqrt2x_ix_j)(\sqrt2y_iy_j)+\sum_{i=1}{n}(\sqrt2x_i)(\sqrt2y_i)+1 \\$

可以看到与线性 SVM 唯一的不同就是：之前的 $(x_i \cdot x_j)$ 变成了 $(\phi(x_i) \cdot \phi(x_j))$ 。

4.2 核函数的作用

我们不禁有个疑问：只是做个内积运算，为什么要有核函数的呢？

这是因为低维空间映射到高维空间后维度可能会很大，如果将全部样本的点乘全部计算好，这样的计算量太大了。

但如果我们有这样的一核函数 $k(x,y) = (\phi(x),\phi(y))$ ， $x_i$ 与 $x_j$ 在特征空间的内积等于它们在原始样本空间中通过函数 k( x, y) 计算的结果，我们就不需要计算高维甚至无穷维空间的内积了。

举个例子：假设我们有一个多项式核函数：

$k(x,y)=(x \cdot y + 1)^2 \\$

带进样本点的后：

$k(x,y) = (\sum_{i=1}^n(x_i \cdot y_i) + 1)^2 \\$

而它的展开项是：

$\sum_{i=1}^nx_i^2y_i^2+\sum_{i=2}^n\sum_{j=1}^{i-1}(\sqrt2x_ix_j)(\sqrt2y_iy_j)+\sum_{i=1}{n}(\sqrt2x_i)(\sqrt2y_i)+1 \\$

如果没有核函数，我们则需要把向量映射成：

$x^{'} = (x_1^2,...,x_n^2,...\sqrt2x_1,...,\sqrt2x_n,1) \\$

然后在进行内积计算，才能与多项式核函数达到相同的效果。

可见核函数的引入一方面减少了我们计算量，另一方面也减少了我们存储数据的内存使用量。

4.3 常见核函数

我们常用核函数有

线性核函数 $k(x_i,x_j) = x_i^Tx_j \\$

多项式核函数 $k(x_i,x_j) = (x_i^Tx_j)^d\\$

高斯核函数 $k(x_i,x_j) = exp(-\frac{||x_i-x_j||}{2\delta^2}) \\$

5.支持向量机回归

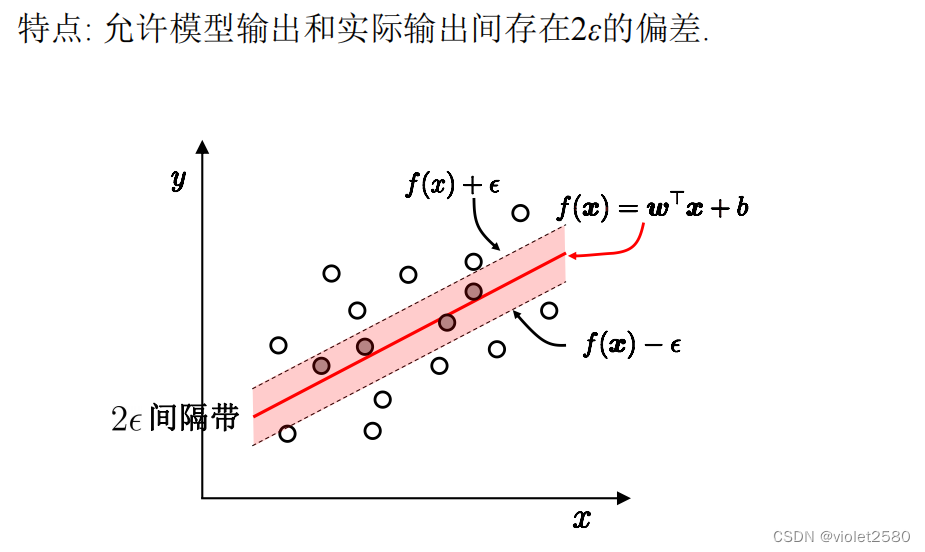
5.1损失函数

5.2形式化

二、支持向量机应用实例

1.SVM实现垃圾邮件分类

具体步骤：

邮件预处理。首先读取样例邮件查看下。然后进行预处理：
1.把整封邮件转化为小写
2.移除所有HTML标签（超文本标记语言）
3.将所有的URL替换为’httpaddr’
4.将所有的地址替换为’emailaddr’
5.将所有数字替换为’number’
6.将所有美元符号($)替换为’dollar’
7.将所有单词还原为词根。例如，“discount”, “discounts”, “discounted” and “discounting”都替换为“discount”
8.移除所有非文字类型，所有的空格(tabs, newlines, spaces)调整为一个空格
然后再对照单词表得到样例对应的序号列。
提取特征。利用序号列得到邮件的一个特征向量，x ∈ R n x\in R^nx∈R
n
，这里是一个1899维的特征向量。
训练SVM。取C=0.1，核函数为线性核，用训练集训练出模型，训练精度为99.8%，再在测试集上测试，精度为98.9%。
打印权重最高的前15个词，邮件中出现这些词更容易是垃圾邮件
用训练好的模型预测已给的四封邮件

代码：


import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import scipy.io as scio
from sklearn import svm 
import re #处理正则表达式的模块
import nltk #自然语言处理工具包'''============================part1 邮件预处理========================='''
#查看样例邮件
f = open('data/emailSample1.txt', 'r').read()
print(f)def processEmail(email):email = email.lower() #转化为小写email = re.sub('<[^<>]+>', ' ', email) #移除所有HTML标签email = re.sub('(http|https)://[^\s]*', 'httpaddr', email) #将所有的URL替换为'httpaddr'email = re.sub('[^\s]+@[^\s]+', 'emailaddr', email) #将所有的地址替换为'emailaddr'email = re.sub('\d+', 'number', email) #将所有数字替换为'number'email = re.sub('[$]+', 'dollar', email) #将所有美元符号($)替换为'dollar'#将所有单词还原为词根//移除所有非文字类型，空格调整stemmer = nltk.stem.PorterStemmer() #使用Porter算法tokens = re.split('[ @$/#.-:&*+=\[\]?!()\{\},\'\">_<;%]', email) #把邮件分割成单个的字符串,[]里面为各种分隔符tokenlist = []for token in tokens:token = re.sub('[^a-zA-Z0-9]', '', token) #去掉任何非字母数字字符try: #porterStemmer有时会出现问题,因此用trytoken = stemmer.stem(token) #词根except:token = ''if len(token) < 1: continue #字符串长度小于1的不添加到tokenlist里tokenlist.append(token)return tokenlist#查看处理后的样例
processed_f = processEmail(f)
for i in processed_f:print(i, end=' ')#得到单词表，序号为索引号+1
vocab_list = np.loadtxt('data/vocab.txt', dtype='str', usecols=1)
#得到词汇表中的序号
def word_indices(processed_f, vocab_list):indices = []for i in range(len(processed_f)):for j in range(len(vocab_list)):if processed_f[i]!=vocab_list[j]:continueindices.append(j+1)return indicesprint("\n")
print("\n")#查看样例序号
f_indices = word_indices(processed_f, vocab_list)
for i in f_indices:print(i, end=' ')
print("\n")
print("\n")'''============================part2 提取特征========================='''
def emailFeatures(indices):features = np.zeros((1899))for each in indices:features[each-1] = 1 #若indices在对应单词表的位置上词语存在则记为1return featuressum(emailFeatures(f_indices)) #45'''============================part3 训练SVM========================='''
#训练模型
train = scio.loadmat('data/spamTrain.mat')
train_x = train['X']
train_y = train['y']clf = svm.SVC(C=0.1, kernel='linear')
clf.fit(train_x, train_y)#精度
def accuracy(clf, x, y):predict_y = clf.predict(x)m = y.sizecount = 0for i in range(m):count = count + np.abs(int(predict_y[i])-int(y[i])) #避免溢出错误得到225return 1-float(count/m) accuracy(clf, train_x, train_y) #0.99825#测试模型
test = scio.loadmat('data/spamTest.mat')
accuracy(clf, test['Xtest'], test['ytest']) #0.989
print("\n")'''============================part4 高权重词========================='''
#打印权重最高的前15个词,邮件中出现这些词更容易是垃圾邮件
i = (clf.coef_).size-1
while i >1883:#返回从小到大排序的索引，然后再打印print(vocab_list[np.argsort(clf.coef_).flatten()[i]], end=' ')i = i-1'''============================part5 预测邮件========================='''t = open('data/spamSample1.txt', 'r').read()
#预处理
processed_f = processEmail(t) 
f_indices = word_indices(processed_f, vocab_list)
#特征提取
x = np.reshape(emailFeatures(f_indices), (1,1899))
#预测
clf.predict(x)

运行结果：

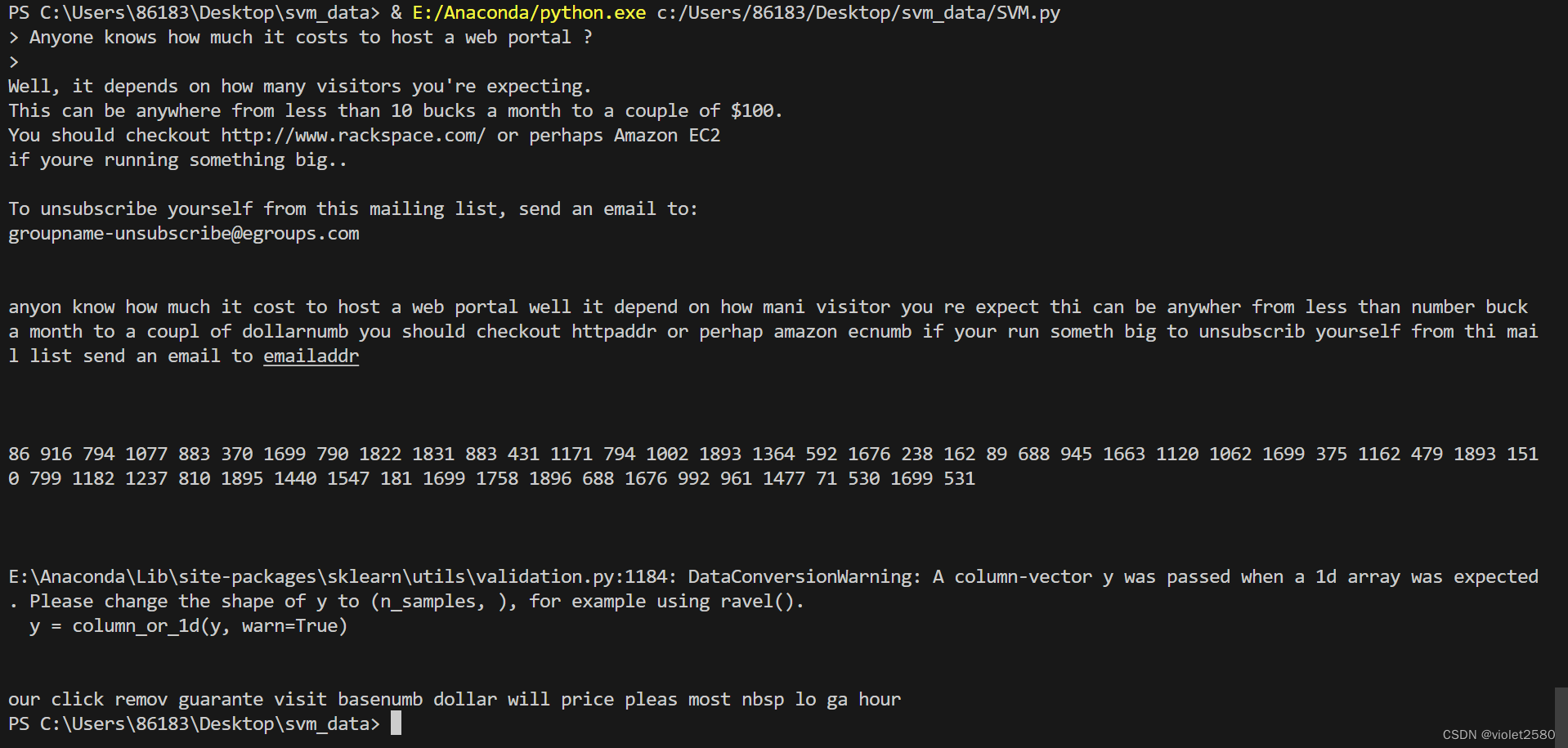
三、总结

支持向量机（Support Vector Machine，SVM）是一种强大的监督学习算法，具有以下特点和广泛的应用方向：

非线性分类能力：SVM通过引入核函数来处理非线性可分的数据，将数据映射到高维空间进行分类，从而具备较强的非线性分类能力。
拟合能力和泛化性能平衡：SVM通过最大化分类边界与训练样本的最小间隔（支持向量），在保证良好拟合能力的同时，具备较高的泛化性能。
鲁棒性和处理高维数据能力：由于SVM主要依赖于支持向量，对于训练集以外的样本变化相对鲁棒，同时能够有效地处理高维数据。
小样本情况下表现优秀：SVM在样本量较少的情况下依然能够保持较好的分类效果，适用于小样本学习问题。
可解释性：SVM通过支持向量和决策边界的定义，提供了对分类结果的解释和理解。

在应用方向上，SVM被广泛应用于以下领域：

机器学习分类和回归任务：SVM在分类和回归问题中都有出色表现，适用于医学诊断、图像识别、文本分类等领域。

支持向量机实验的主要步骤包括数据准备、特征工程、数据预处理、数据集划分、核函数选择、模型训练和调优、模型评估、结果分析、可视化展示以及模型应用。在其中，对偶形式的SVM算法可以用于求解大规模问题，并通过引入核函数来处理非线性可分的数据。核函数的选择对于模型的性能至关重要，可以根据问题的特点选择合适的核函数类型，如线性核、多项式核、高斯核等。通过实验的整体过程，可以得出SVM模型在具体数据集上的分类性能，并为实际应用提供指导。

这篇关于机器学习实验课7 支持向量机（SVM）的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

机器学习实验课7 支持向量机（SVM）

一、SVM原理

1.间隔与支持向量

1.1线性可分

1.2支持向量

1.3SVM最优化

2.对偶问题

2.1拉格朗日乘数法

2.2 不等式约束优化问题

2.2 强对偶性

2.3.SVM 优化

3.软间隔与正则化

3.1 解决问题

3.2 优化目标及求解

4.核函数

4.1 线性不可分

4.2 核函数的作用

4.3 常见核函数

5.支持向量机回归

5.1损失函数

5.2形式化

二、支持向量机应用实例

1.SVM实现垃圾邮件分类

具体步骤：

代码：

运行结果：

三、总结

相关文章

HarmonyOS学习(七)——UI（五）常用布局总结

Ilya-AI分享的他在OpenAI学习到的15个提示工程技巧

【前端学习】AntV G6-08 深入图形与图形分组、自定义节点、节点动画（下）

学习hash总结

【Prometheus】PromQL向量匹配实现不同标签的向量数据进行运算

零基础学习Redis(10) -- zset类型命令使用

【机器学习】高斯过程的基本概念和应用领域以及在python中的实例

【学习笔记】陈强-机器学习-Python-Ch15 人工神经网络（1）sklearn

系统架构师考试学习笔记第三篇——架构设计高级知识（20）通信系统架构设计理论与实践

线性代数|机器学习-P36在图中找聚类

机器学习 实验课7 支持向量机（SVM）

一、SVM原理

1.间隔与支持向量

1.1线性可分

1.2支持向量

1.3SVM最优化

2.对偶问题

2.1拉格朗日乘数法

2.2 不等式约束优化问题

2.2 强对偶性

2.3.SVM 优化

3.软间隔与正则化

3.1 解决问题

3.2 优化目标及求解

4.核函数

4.1 线性不可分

4.2 核函数的作用

4.3 常见核函数

5.支持向量机回归

5.1损失函数

5.2形式化

二、支持向量机应用实例

1.SVM实现垃圾邮件分类

具体步骤：

代码：

运行结果：

三、总结

相关文章

机器学习实验课7 支持向量机（SVM）