火箭回收的分析

机器人和人工智能的最新发展使我们能够解决长期以来被认为困难或无法解决的问题。行星软着陆问题是最近再次引起人们关注的最优控制理论问题之一。

本文介绍了一种开发控制系统的通用方法，该方法可应用于广泛的机器人应用，不一定是火箭。我们将以类似于 SpaceX Falcon9 的火箭为例，逐步完成机器人控制系统的分析和设计的所有主要步骤。

模型假设

让我们构建一个简单的火箭模型并探索其着陆行为。首先我们假设没有空气摩擦。当然，我们可以考虑它，但是，我们将忽略它，只是为了使模型尽可能简单而不牺牲准确性。

此外，让我们忽略火箭质量不是恒定的。Falcon9 着陆时消耗约 200 公斤燃料。我们将模拟着陆轨迹的最后几秒，因此我们可以认为质量是恒定的。

最后，让我们只考虑二维空间中的动力学，这意味着我们可以假设第三个坐标不需要控制，或者换句话说，沿该轴的误差为零。我们稍后可以添加第三个坐标。这没有什么大的区别，但是在 2D 中，更容易观察对象的行为。

火箭动力学

让我们假设火箭第一级的 9 个发动机中只有 3 个用于控制 XZ 飞机上的火箭。因此，我们的推力将被分成两个角度稍有不同的矢量a和(a + u)

我们在方程中添加了一些由随机变量γ定义的噪声，其中D是相对引擎之间的距离。

因此，从初始条件q = (x, ẋ, z, ż, a, ş)和定义的函数Fth(q, t)和u(q, t)开始，我们可以模拟火箭的行为。让我们从寻找火箭推力函数开始。

火箭推力

想象一下我们考虑相反的问题。火箭以恒定推力Fth起飞。其高度和垂直速度可由以下方程求得：

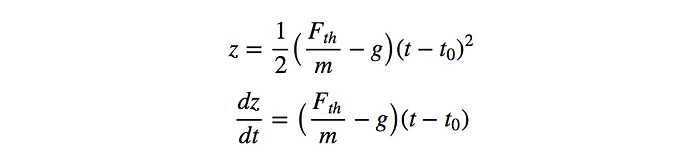
因此，向后求解，我们可以轻松找到给定初始条件 z 和 ż所需的推力Fth：

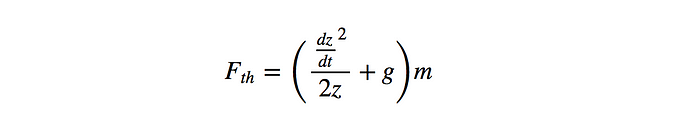
让我们模拟并检查它在初始条件下的工作原理：
x = 1.5m , ẋ = 0.5 m/s
z = 231m, ż =-50m/s ,
a = 0, ş = 0

由于最终水平速度不够小，着陆失败。然而，火箭的垂直速度接近于零，这是很大的。

发动机角度控制器

现在让我们开发一个控制器，使定义火箭运动的其余变量接近于零。换句话说，我们需要找到一个函数 u = u( x, ẋ, z, ż, a, ş) ，它将使所有从给定初始条件开始的轨迹都到达接近 (0, 0, 0 , 0, 0, 0)。

幸运的是，当火箭角度a足够小时，描述火箭运动的方程几乎是线性的。我们可以在线性化后重写它们，如下所示：

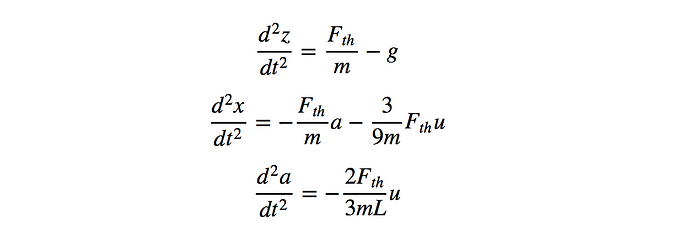
现在让我们看看所谓的 LQR 控制器，它是一种强大的方法，用于寻找可由一阶线性微分方程描述的系统的最佳控制。（https://en.wikipedia.org/wiki/Linear%E2%80%93quadratic_regulator）

线性QR

由于我们已经找到了 z 的控制器，我们需要的只是求解另外两个变量x和a。引入 v= ẋ和w=ş作为新变量，我们可以降低微分方程的阶数，如下所示：

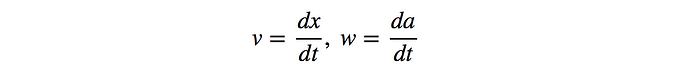
因此，等式将如下所示：

或者

LQR 允许我们以 u = -K p 的形式求出，其中 K 是一个矩阵，它最小化了二次成本函数，定义为：

Q 和 R 应该是正定矩阵。通常，对于Q和R我们可以选择对角矩阵。让我们为 Q 选择一个对角元素为 [0.5, 10, 1, 1] 的矩阵，为 R 选择秩为 1 的单位矩阵。我们为 x 选择一个较小的数字，为ẋ选择一个大 20 倍的数字，因为 x 与零的偏差为对于成功着陆而言不像水平速度那么敏感。在下图中，我们可以看到x坐标5m的误差根本不是问题。

例如，如果使用 python，您可能会在 scipy.linalg 库中找到 LQR 求解器。

您可能会注意到矩阵 (A-BK) 的任何特征值的实部都是负数，这意味着找到的控制 u = -Kq 是稳定的。

现在让我们用找到的 LQR 控制器模拟火箭的行为：

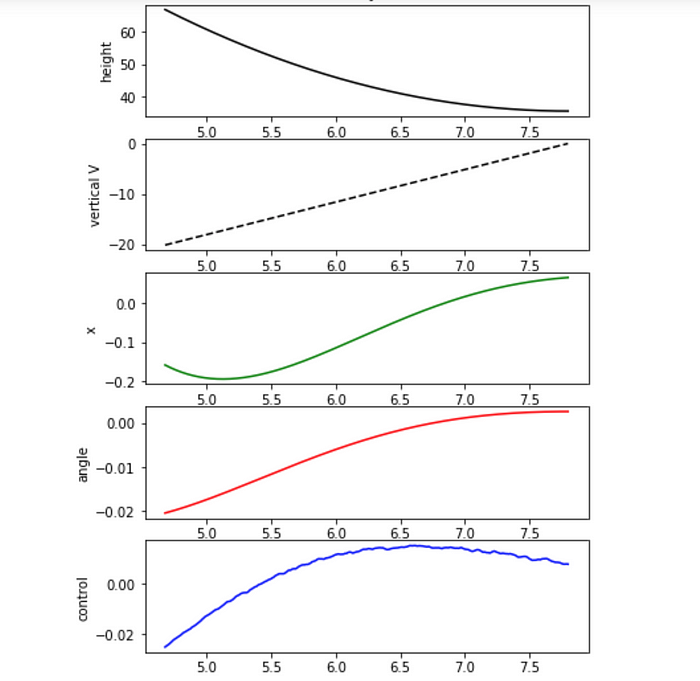
以及火箭弹道的侧视图和对应的发动机角度u函数：

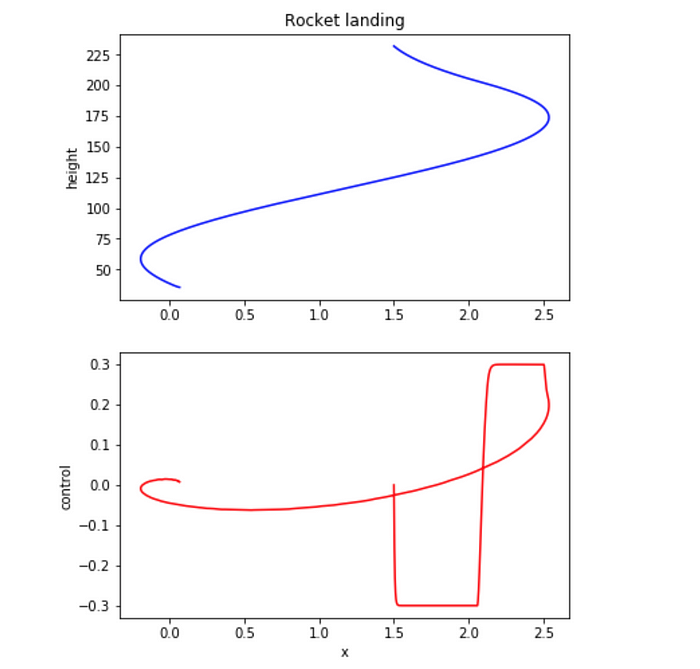
结论

总而言之，我想谈谈开发机器人控制系统的一般方法。第一步始终是构建模型。当您拥有模型后，您可以使用它，更改初始条件、机器人参数等。此分析可以帮助您了解挑战是什么或问题出在哪里。

然后，您可以开始设计控制器，了解您想要解决的问题类型。最后你可能会想出不同的机器人设计。