本文主要是介绍离散数学-存在量词 为啥必须使用合取式函数?,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
1.存在量词:
代表在个体域讨论范围中---》存在一部分 一些指定的个体或者抽象的客体;
2.那么我们开始正式环节;
-》有些人是男同学 --》咱们使用存在量词+合取范式进行得到命题函数 -》
》存在一个变元 "X" 个体变元 -- 并且变元x
》1.拆分:原有命题得到 x是人 x是男同学 。我们使用 存在量词 合取式得到的命题为 
存在有些x x是人 并且x也是男同学。真命题时 当且仅当 存在有些男同学 没有什么问题 。
2.如果我们使用 全称量词一样 中间使用 条件 命题连接词;
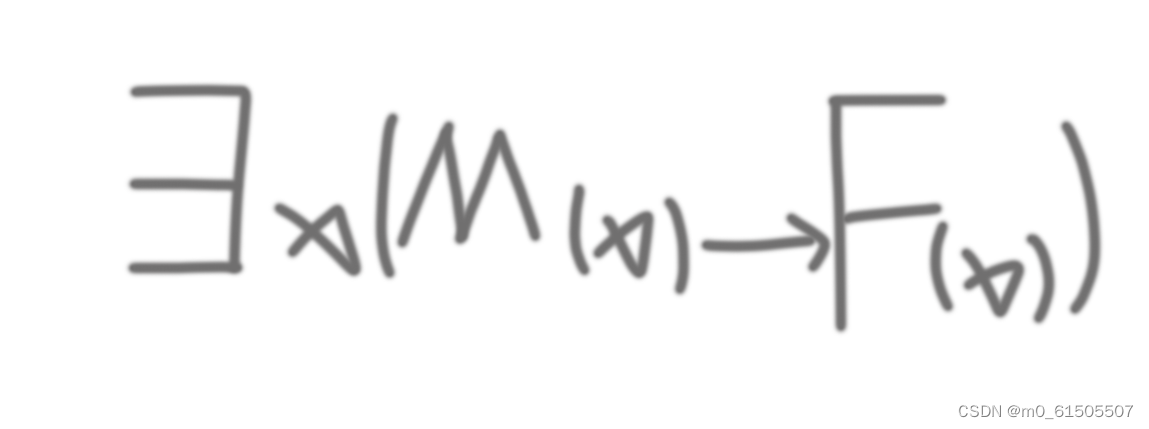
当然都是格式都是合式公式;那么含义为 存在有些x 如果x是人 则x是男同学;命题为真时
当且仅当x是男同学 或者 x是人且x是男同学 或者 x不是人且x也不是男同学;命题函数含义完全不一致;命题的成真 也不一致。
所以在使用存在量词 我们使用 合取连接式 进行表达命题函数。
看到这里解释完毕 为啥使用 合取 表达存在量词的命题函数。 ---------------------------
那么咱们看看全称量词 如果 合取来表达
》1.人都会死
个体变元 x ;拆分:x是人 ,x会死 两个量词;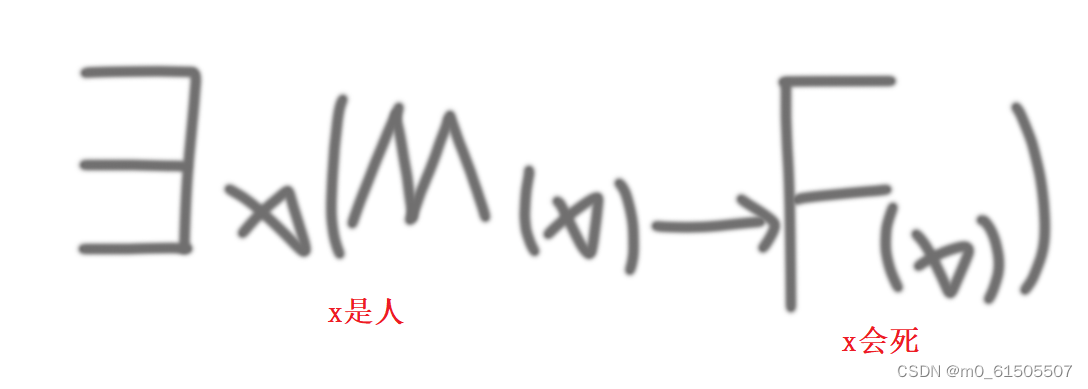
对于所有/任意/凡是/变元x x是人则x会死 条件 连接词 没有问题。为真 当且仅当 x会死 同或 x是人且x会死 同或 x不是人 且 x不会死;真值含义.
全称量词含义为:存在任何以x为人的个体变元 则x都会死;
“人都会死”是用全称量词+条件式写出来的, 即“对于任意对象x, 如果x是人, 那么x会死”, 这句话为真当且仅当所以为人的对象x都会死.
合取表示:任何x的个体变元 x是人且x会死 没有指定x的条件 x代表包括人的所有对象。x是人且x(所有对象)会死。
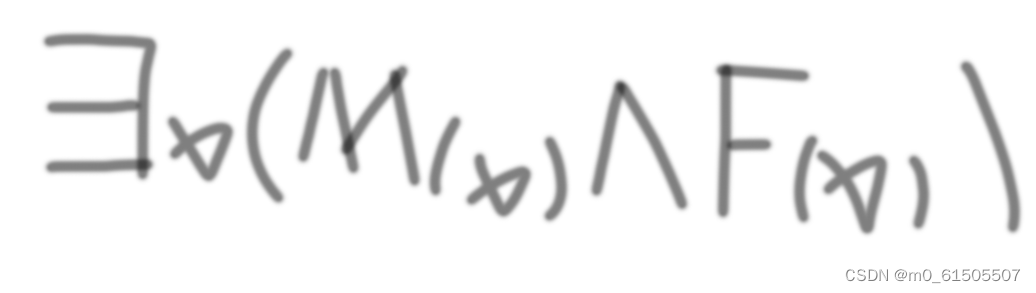 写的有不好的地方 您多多指点~~ 感谢 ~ 下面放着大佬的文章 详细查收
写的有不好的地方 您多多指点~~ 感谢 ~ 下面放着大佬的文章 详细查收
有兴趣 可以关注点赞 冲冲冲~
存在量词后必须用合取式?-数学_存在即合取-CSDN博客语法上没有错误, 都是well-formed formula, 但是语义上与一般用自然语言表达出来的语义不符. 例:“有一个男学生”是用存在量词+合取式写出来的, 即“存在一个对象x, x是男的且x是学生”. 这句话为真当且仅当存在一个男学生如果我们用存在量词+条件式写出来, 则是“存在一个对象x, 如果x是男的则x是学生”. 注意这段话为真, 当且仅当x不是男的或者x是学生. 同样, “人都会死..._存在即合取https://blog.csdn.net/kyle1314608/article/details/105735189
这篇关于离散数学-存在量词 为啥必须使用合取式函数?的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!






