NOIP2014提高组day2-T2：寻找道路

本文主要是介绍NOIP2014提高组day2-T2：寻找道路，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

题目链接

[NOIP2014 提高组] 寻找道路

题目描述

在有向图 $G$ 中，每条边的长度均为 $1$ ，现给定起点和终点，请你在图中找一条从起点到终点的路径，该路径满足以下条件：

路径上的所有点的出边所指向的点都直接或间接与终点连通。
在满足条件 $1$ 的情况下使路径最短。

注意：图 $G$ 中可能存在重边和自环，题目保证终点没有出边。

请你输出符合条件的路径的长度。

输入格式

第一行有两个用一个空格隔开的整数 $n$ 和 $m$ ，表示图有 $n$ 个点和 $m$ 条边。

接下来的 $m$ 行每行 $2$ 个整数 $x, y$ ，之间用一个空格隔开，表示有一条边从点 $x$ 指向点 $y$ 。

最后一行有两个用一个空格隔开的整数 $s, t$ ，表示起点为 $s$ ，终点为 $t$ 。

输出格式

输出只有一行，包含一个整数，表示满足题目描述的最短路径的长度。如果这样的路径不存在，输出 $- 1$ 。

样例 #1

样例输入 #1

样例输出 #1

-1

样例 #2

样例输入 #2

样例输出 #2

提示

样例 1 解释

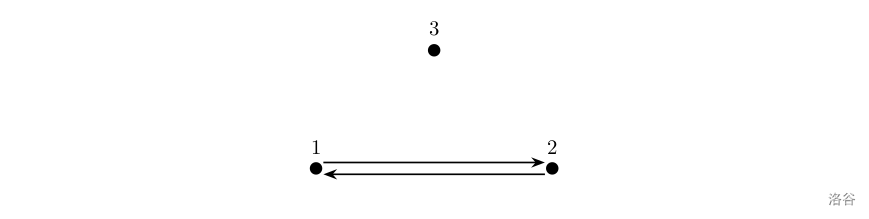
如上图所示，箭头表示有向道路，圆点表示城市。起点 $1$ 与终点 $3$ 不连通，所以满足题目描述的路径不存在，故输出 $- 1$ 。

样例 2 解释

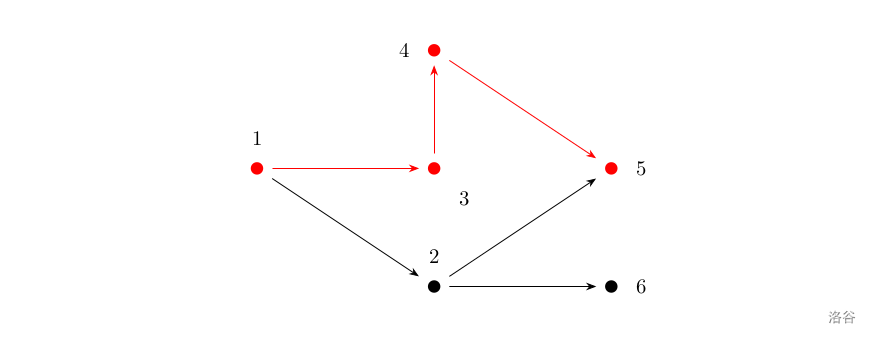
如上图所示，满足条件的路径为 $1\to 3\to 4\to 5$ 。注意点 $2$ 不能在答案路径中，因为点 $2$ 连了一条边到点 $6$ ，而点 $6$ 不与终点 $5$ 连通。

数据范围及约定

对于 $30\%$ 的数据， $0<n\le10$ ， $0<m\le 20$ 。
对于 $60\%$ 的数据， $0<n\le100$ ， $0<m\le 2000$ 。
对于 $100\%$ 的数据， $0<n\le 10^4$ ， $0<m\le 2\times 10^5$ ， $0<x,y,s,t\le n,x,s\ne t$ 。

算法思想

根据题目描述，要求的是满足下面条件的最短路径的长度：

路径上的所有点的出边所指向的点都直接或间接与终点连通

也就是说，该路径上的每个点都能走到终点。那么有哪些点满足条件呢？

首先可以从终点开始反向搜索所有能够达到的点 $i$ ，将其状态 $s t [i]$ 设置为true
其次遍历每个点 $i$ ，如果其所有出边所指向的点的状态都为true，那么点 $i$ 满足条件

当筛选出来所有满足条件的点后，可以通过bfs求起点到终点的最短路径了。

注意，由于正向和反向都要处理，因此需要双向建边，那么如何区分正向边和反向边呢？可以使用链式前向星来保存图，按顺序添加边时，偶数为正向边，奇数为反向边。

时间复杂度

从终点开始反向搜索所有能够达到的点，每条边只会遍历一次，时间复杂度为 $O (n + m)$ 。
遍历每个点，处理其所有出边，时间复杂度为 $O (n + m)$
bfs求最短路径，时间复杂度为 $O (n + m)$

代码实现

#include <iostream>
#include <cstring>
#include <queue>
using namespace std;
const int N = 1e4 + 5, M = 4e5 + 5;
int h[N], e[M], ne[M], idx;
int dis[N];
bool st[N], f[N];
void add(int a, int b)  // 添加一条边a->b
{e[idx] = b, ne[idx] = h[a], h[a] = idx ++ ; //正向边是偶数，反向边是奇数
}void dfs(int u)
{st[u] = true;for(int i = h[u]; ~ i; i = ne[i]){if(i % 2 == 0) continue; //只搜索反向边int v = e[i];if(!st[v]) dfs(v);}
}int bfs(int s, int t)
{if(!f[s]) return -1; //起点不满足条件memset(dis, 0x3f, sizeof dis);queue<int> q;q.push(s), dis[s] = 0;while(q.size()){int u = q.front(); q.pop();if(u == t) return dis[u];for(int i = h[u]; ~ i; i = ne[i]){if(i % 2) continue; //只搜索正向边int v = e[i];if(!f[v]) continue; //不满足条件if(dis[v] > dis[u] + 1){dis[v] = dis[u] + 1;q.push(v);}}}return -1;
}int main()
{int n, m, s, t;scanf("%d%d", &n, &m);memset(h, -1, sizeof h);while (m -- ){int a, b;scanf("%d%d", &a, &b);add(a, b), add(b, a); //双向建边}scanf("%d%d", &s, &t);dfs(t); //反向搜索每个点的状态//处理每个点出边所指向的点for(int i = 1; i <= n; i ++){f[i] = true;for(int j = h[i]; ~ j; j = ne[j]){//只判断正向边if(j % 2 == 0 && !st[e[j]]){f[i] = false; //i点不满足条件break;}}}//搜索最短路径printf("%d\n", bfs(s, t));return 0;
}