本文主要是介绍“寻根问祖”深度学习只需六段代码,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
更多深度文章,请关注:https://yq.aliyun.com/cloud
本文涵盖了每段代码的发明人及其突破背景。每个故事都有GitHub上的简单代码示例。

1.最小二乘法:
最小二乘法(又称最小平方法)是一种数学优化技术。它通过最小化误差的平方和寻找数据的最佳函数匹配。利用最小二乘法可以简便地求得未知的数据,并使得这些求得的数据与实际数据之间误差的平方和为最小。最小二乘法还可用于曲线拟合。
深度学习最先开始于这个数学片段,可能你觉得很奇怪,但是事实就是如此。(我用Python实现它):
# y = mx + b
# m is slope, b is y-intercept
def compute_error_for_line_given_points(b, m, coordinates):totalError = 0for i in range(0, len(coordinates)):x = coordinates[i][0]y = coordinates[i][1]totalError += (y - (m * x + b)) ** 2return totalError / float(len(coordinates))
# example
compute_error_for_line_given_points(1, 2, [[3,6],[6,9],[12,18]])
最小二乘法是由巴黎数学家阿德里安·玛丽·勒让德(1805年,勒让德)首次提出的,他也是以测量仪器而闻名的数学家。他对预测彗星的未来位置特别痴迷,鉴于彗星以前的几个位置,他准备创建一种计算其轨迹的方法。
他尝试了几种方法后,然后一个方法终于难住了他。Legendre的过程是通过猜测彗星的未来位置而开始的,通过记录数据,分析,最后通过数据验证了他的猜测,以减少平方误差的总和。这是线性回归的种子。
在我提供的代码你可以更好理解最小二乘法。m是系数,b是你的预测的常数,所求坐标是彗星的位置。目标是找到m和b的组合,其中错误尽可能小。
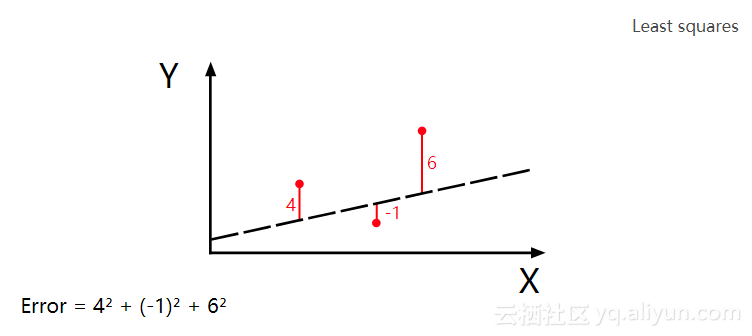
其实深度学习的核心就是:采取输入和期望的输出,然后搜索两者之间的相关性。
2.梯度下降:
Legendre的手动尝试降低错误率的方法是耗时的。荷兰诺贝尔奖得主彼得·德比(Peter Debye)在一个世纪后(1909年,德拜)正式发布了这一缺陷的解决方案。
让我们想象一下Legendre正在苦恼一个参数,我们把它叫做X。Y轴表示X的每个值的误差值。Legendre正在搜索X以寻找到错误最低的位置。在这种图形化表示中,我们可以看到X最小化的X值是X = 1.1时。
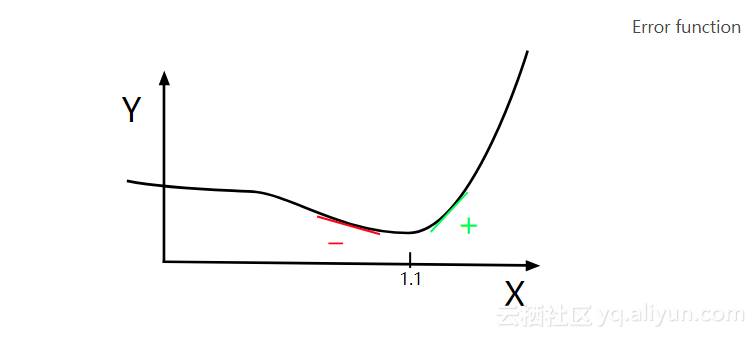
彼得·德比(Peter Debye)注意到最低点左边的斜率是负的,而另一边则是正的。因此,如果你知道任何给定X值的斜率值,你可以将Y指向最小值。
这导致了梯度下降的方法。这个原则几乎在每一个深度学习模式中使用。要玩这个,我们假设错误函数是 Error = x ^ 5-2x ^ 3-2。要知道任何给定X值的斜率,我们取其导数,即5x ^ 4 - 6x ^ 2:
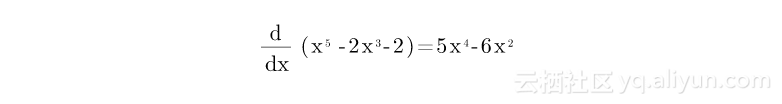
这个数学片段用Python实现:
current_x = 0.5 # the algorithm starts at x=0.5
learning_rate = 0.01 # step size multiplier
num_iterations = 60 # the number of times to train the function
#the derivative of the error function (x**4 = the power of 4 or x^4)
def slope_at_given_x_value(x): return 5 * x**4 - 6 * x**2
# Move X to the right or left depending on the slope of the error function
for i in range(num_iterations):previous_x = current_xcurrent_x += -learning_rate * slope_at_given_x_value(previous_x)print(previous_x)
print("The local minimum occurs at %f" % current_x)
这里的技巧是learning_rate。通过沿斜坡的相反方向接近最小值。此外,越接近最小值,斜率越小。当斜率接近零时,这会减少每个步骤。
num_iterations在达到最低限度之前,你可以预计你的迭代次数。用参数来获得梯度下降的感觉。
3.线性回归:
通过组合最小二乘法和梯度下降法,你可以得到线性回归。在20世纪50年代和60年代,一批经济学家在早期的计算机上实现了这些想法。这个逻辑是在实体机打卡上实现的——真正的手工软件程序。大约需要几天的时间准备这些打孔卡,最多24小时才能通过计算机进行一次回归分析。
下面是一个线性回归示例转换为Python语言:
#Price of wheat/kg and the average price of bread
wheat_and_bread = [[0.5,5],[0.6,5.5],[0.8,6],[1.1,6.8],[1.4,7]]def step_gradient(b_current, m_current, points, learningRate):b_gradient = 0m_gradient = 0N = float(len(points))for i in range(0, len(points)):x = points[i][0]y = points[i][1]b_gradient += -(2/N) * (y - ((m_current * x) + b_current))m_gradient += -(2/N) * x * (y - ((m_current * x) + b_current))new_b = b_current - (learningRate * b_gradient)new_m = m_current - (learningRate * m_gradient)return [new_b, new_m]
def gradient_descent_runner(points, starting_b, starting_m, learning_rate, num_iterations):b = starting_bm = starting_mfor i in range(num_iterations):b, m = step_gradient(b, m, points, learning_rate)return [b, m]
gradient_descent_runner(wheat_and_bread, 1, 1, 0.01, 100)这没有引入任何新的知识。然而,将误差函数与渐变下降合并可能对一些人有一点困扰。你可以运行代码,慢慢思考这里面的逻辑。
4.感知器:
弗兰克·罗森布拉特(Frank Rosenblatt)这个怪才字白天解剖大鼠的大脑,在夜间寻找外星生命的迹象。在1958年,他发布了一个模仿神经元的机器(1958年,罗森布拉特)的“纽约时报”的头版“ 新海军装备学习 ” 。
如果你展示了Rosenblatt机器的50套两张图像,其中一张标有左图,另一张在右侧,你可以在不预编程的情况下进行区分。
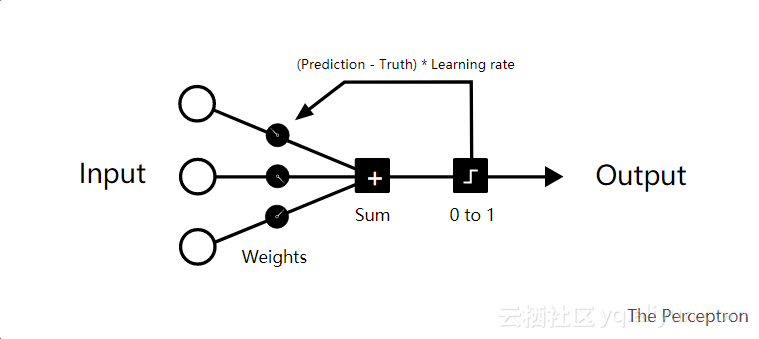
对于每个训练周期,你从左侧输入数据。初始随机权重添加到所有输入数据。然后总结出来。如果总和为负数,则将其转换为0否则映射到1。
如果预测是正确的,那么该循环中的权重就没有任何反应。如果这是错误的,你可以将错误乘以学习率。这相应地调整权重。
让我们用经典OR逻辑运行感知器。
| 输入 | 产量 | |
| 0 | 0 = | 0 |
| 0 | 1 = | 1 |
| 1 | 0 = | 1 |
| 1 | 1 = | 1 |
感知器Python代码实现:
from random import choice
from numpy import array, dot, random
1_or_0 = lambda x: 0 if x < 0 else 1
training_data = [ (array([0,0,1]), 0), (array([0,1,1]), 1), (array([1,0,1]), 1), (array([1,1,1]), 1), ]
weights = random.rand(3)
errors = []
learning_rate = 0.2
num_iterations = 100
for i in range(num_iterations): input, truth = choice(training_data) result = dot(weights, input) error = truth - 1_or_0(result) errors.append(error) weights += learning_rate * error * input for x, _ in training_data: result = dot(x, w) print("{}: {} -> {}".format(input[:2], result, 1_or_0(result)))
感知器最初炒作一年之后,马文·明斯基和西摩·帕普特(Seymour Papert)摧毁了这个想法(1969年,明斯基和帕普特)。当时,明斯基和帕普特都在麻省理工学院的AI实验室工作。他们写了一本书,证明感知器只能解决线性问题。他们还揭露了关于多层感知器的缺陷。
在明斯基和帕普特书籍出版一年之后,芬兰的一名大学生发现了解多层感知器的非线性问题的理论(Linnainmaa,1970)。由于马文·明斯基和西摩·帕普特的影响力,关于AI的研究大部分都停止了。这被称为第一个AI冬天。
明斯基和帕普特的批评是异端问题。逻辑与OR逻辑相同,但有一个例外:当有两个true语句(1&1)时,返回False(0)。
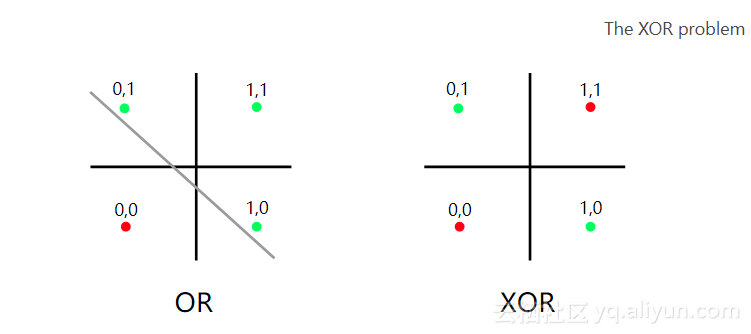
在OR逻辑中,可以将真实组合与虚假组合分开。但是从上图你可以看到,你不能将XOR逻辑与一个线性函数进行分割。
5.人工神经网络:
到1986年,几项实验证明,神经网络可以解决复杂的非线性问题(Rumelhart等,1986)。而且当时的计算能力比预期的发展的要快,这就是Rumelhart等人 介绍了他们的传奇论文:
我们描述了一种新的神经元网络学习过程,反向传播。该过程通过重复调整网络中的连接的权重,以便最小化网络的实际输出向量与期望的输出向量之间的差异的度量。由于权重调整的结果,不属于输入或输出的而是内部“隐藏”单元来完成的,并且任务中的规则由这些单元的交互制定。例如感知器收敛过程。Nature323,533-536(1986年10月9日)。
为了理解论文的核心,我们将用DeepMind的Andrew Trask编写来帮助我们理解。这不是一个随机的代码段。它曾被用于斯坦福大学Andrew Karpathy的深度学习课程,以及Siraj Raval的Udacity课程。除此之外,它解决了XOR问题,也解冻了第一个AI冬天。
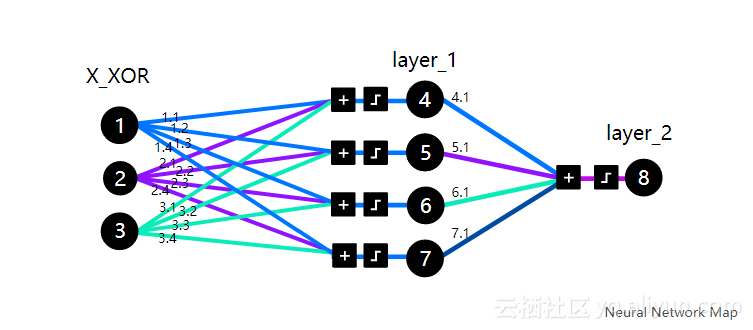
在我们编写代码之前,需要一到两个小时来掌握核心逻辑,然后阅读Trask的博客文章。请注意,X_XOR数据中添加的参数[1]是偏置神经元,它们与线性函数中的常量具有相同的行为。
import numpy as np
X_XOR = np.array([[0,0,1], [0,1,1], [1,0,1],[1,1,1]])
y_truth = np.array([[0],[1],[1],[0]])
np.random.seed(1)
syn_0 = 2*np.random.random((3,4)) - 1
syn_1 = 2*np.random.random((4,1)) - 1
def sigmoid(x):output = 1/(1+np.exp(-x))return output
def sigmoid_output_to_derivative(output):return output*(1-output)
for j in range(60000):layer_1 = sigmoid(np.dot(X_XOR, syn_0))layer_2 = sigmoid(np.dot(layer_1, syn_1))error = layer_2 - y_truthlayer_2_delta = error * sigmoid_output_to_derivative(layer_2)layer_1_error = layer_2_delta.dot(syn_1.T)layer_1_delta = layer_1_error * sigmoid_output_to_derivative(layer_1)syn_1 -= layer_1.T.dot(layer_2_delta)syn_0 -= X_XOR.T.dot(layer_1_delta)print("Output After Training: \n", layer_2)
反向传播,矩阵乘法和梯度下降组合可能很难理解。我们只需专注于理解背后的逻辑,不需要关注其他东西。
另外,可以看看安德鲁·卡尔皮斯(Andrew Karpathy)关于反向传播的演讲,并阅读了迈克尔·尼尔森(Michael Nielsen)关于它的第一章,或许这能够帮助你理解。
6.深层神经网络:
深层神经网络是输入层和输出层之间具有多层的神经网络。这个概念由Rina Dechter(Dechter,1986)介绍,但在2012年才开始获得了主流关注。
深层神经网络的核心结构基本保持不变,但现在应用于几个不同的问题,专业化也有很多改进。最初,这是一组数学函数来简化嘈杂的地球数据(Tikhonov,AN,1963)。他们现在正在使用神经网络,以提高其泛化能力。
计算能力的提升也是其大火的原因之一。一个超级计算机在八十年代中期计算一年的计算量而在今天的GPU技术的帮助下需要半秒钟就OK了。
计算方面的成本降低以及深度学习库的发展,深层神经网络结构正在被大多数人接受使用。我们来看一个普通的深层学习堆栈的例子,从底层硬件开始介绍:
- GPU: Nvidia特斯拉K80。硬件常用于图形处理。与CPU相比,深度学习平均速度要快50-200倍。
- CUDA :GPU的低级编程语言
- CuDNN : Nvidia的库来优化CUDA
- Tensorflow :Google在CuDNN之上的深层学习框架
- TFlearn :Tensorflow的前端框架
我们先来看看MNIST图像分类的数字,这是深度学习的“Hello World”
在TFlearn实施:
from __future__ import division, print_function, absolute_import
import tflearn
from tflearn.layers.core import dropout, fully_connected
from tensorflow.examples.tutorials.mnist import input_data
from tflearn.layers.conv import conv_2d, max_pool_2d
from tflearn.layers.normalization import local_response_normalization
from tflearn.layers.estimator import regression
# Data loading and preprocessing
mnist = input_data.read_data_sets("/data/", one_hot=True)
X, Y, testX, testY = mnist.train.images, mnist.train.labels, mnist.test.images, mnist.test.labels
X = X.reshape([-1, 28, 28, 1])
testX = testX.reshape([-1, 28, 28, 1])
# Building convolutional network
network = tflearn.input_data(shape=[None, 28, 28, 1], name='input')
network = conv_2d(network, 32, 3, activation='relu', regularizer="L2")
network = max_pool_2d(network, 2)
network = local_response_normalization(network)
network = conv_2d(network, 64, 3, activation='relu', regularizer="L2")
network = max_pool_2d(network, 2)
network = local_response_normalization(network)
network = fully_connected(network, 128, activation='tanh')
network = dropout(network, 0.8)
network = fully_connected(network, 256, activation='tanh')
network = dropout(network, 0.8)
network = fully_connected(network, 10, activation='softmax')
network = regression(network, optimizer='adam', learning_rate=0.01,loss='categorical_crossentropy',
name='target')
# Training
model = tflearn.DNN(network, tensorboard_verbose=0)
model.fit({'input': X}, {'target': Y}, n_epoch=20,validation_set=({'input': testX}, {'target': testY}),snapshot_step=100, show_metric=True, run_id='convnet_mnist')
有很多不错的文章介绍MNIST:这里 这里和这里。
总结:
我认为:深度学习的主要逻辑仍然类似于Rosenblatt的感知器。而不是使用Heaviside二进制步骤功能,今天神经网络大多使用Relu激活。在卷积神经网络的最后一层,损失等于categorical_crossentropy。这是勒布雷最小平方的演变,是多类别的逻辑回归。优化器adam源于德拜梯度下降的工作。或许有了这些认识,我们才可以更好的进行深度学习的研究。
希望上述能够帮助到你!
本文由北邮@爱可可-爱生活老师推荐,@阿里云云栖社区组织翻译。
文章原标题《Coding the History of Deep Learning》
作者Emil Wallner 曾经执教于牛津大学商学院,现在正致力于技术教育。
译者:袁虎 审阅:
文章为简译,更为详细的内容,请查看原文
这篇关于“寻根问祖”深度学习只需六段代码的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!





