Domain Adaptation 相关介绍

本文主要是介绍Domain Adaptation 相关介绍，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

1. Transfer Learning

Transfer learning 是机器学习的一个分支, 而 Domain adpatation 是 transfer learning 的一个分支.
在 transfer learning 中有两个概念: source domain (源域) 和 target domain (目标域).
源域中往往有丰富的信息, 比如有大量的数据点和其真实的标签; 但目标域中相反, 数据不带有标签或少量数据带有标签, 所以无法用传统的方式学习. Transfer learning 的目标是: 利用两个域的信息, 学习一个能在 target domain 上准确率高的分类器.

根据两个域的背景设定不同, transfer learning 有以下分类, 本文关注于 domain adaptation.

上图来自于综述论文 A survey on domain adaptation theory: learning bounds and theoretical guarantees.

• 传统的学习设定: 两个域的输入分布相同, 且任务相同. 这时的 source domain 就是训练集, target domain 就是测试集.
• Inductive transfer learning: 两个域的输入分布相同, 但任务不同.
• Transductive transfer learning/ Domain adaptation: 两个域的输入分布不同, 但任务相同.
• Unsupervised transfer learning: 两个域的输入分布不同, 且任务不同.

所以在 Domain adaptation 任务中, source domain 与 target domain 是不同的, 这种差别称为: distributional change, distributional shift 或 domain shift. 下面介绍下 domain shift.

2. Domain Shift

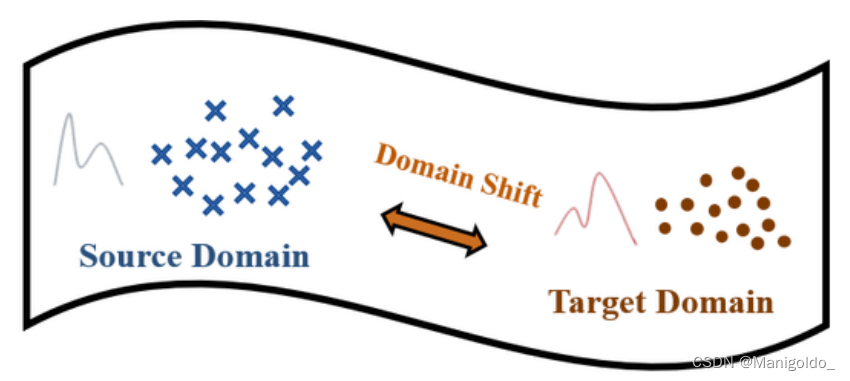
Domain shift 主要分为以下三种: prior shift, covariate shift 和 concept shift.

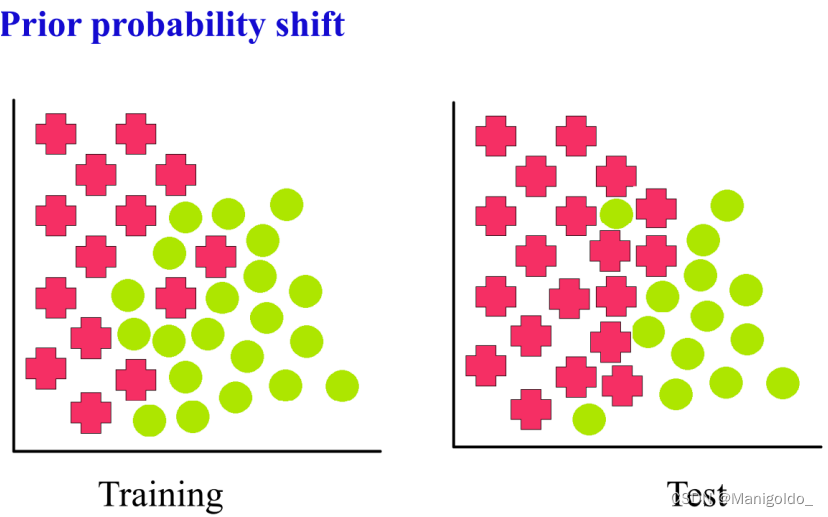
2.1 Prior shift

用于 $Y\to X$ problems, 设定为:

• posterior distributions are equivalent: $p_s(x|y)=p_t(x|y)$
• prior distributions of classes are different: $p_s(y)\ne p_t(y)$

2.2 Covariate shift

用于 $X\to Y$ problems, 设定为:

• marginal distributions are different: $p_s(x)\ne p_t(x)$
• conditional distributions are equivalent: $p_s(y|x)=p_t(y|x)$

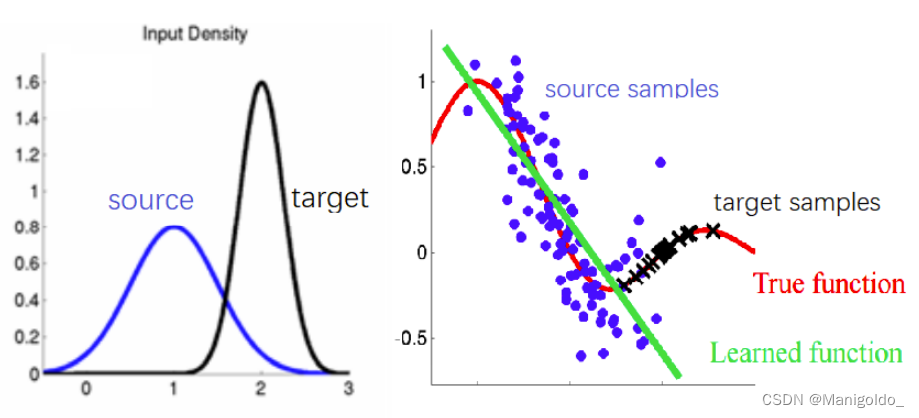
Covariate shift 是最常见的设定, 大多domain adaptation 的论文都是以这个为背景. 上图是一个例子, source 与 target 的分布不同(左图), 但它们的样本点都坐落在 true function 的周围(右图), 如果只用 source samples 做训练可能会得到绿色的函数, 无法用在 target domain上.

2.3 Concept shift

又叫 Data drift, 用于 $X\to Y$ 和 $Y\to X$ problems.

• In $X\to Y$ problems: $p_s(x)=p_t(x)$ and $p_s(y|x)\ne p_t(y|x)$
• In $Y\to X$ problems: $p_s(y)=p_t(y)$ and $p_s(x|y)\ne p_t(x|y)$

3. Closed-set Unsupervised Domain Adaptation

Domain Adaptation 其实也有很多类型, 比如 closed-set 或 open-set, unsupervised 或 supervised. 研究最多的是 closed-set unsupervised domain adaptation. 每个单词的意思是:

• Domain Adaptation(DA): 正如前面讲的, source 与 target domain 的分布不同, 但任务相同
• Unsupervised DA: target domain 中的数据不带有标签
• Closed-set DA (traditional DA): source 与 target domain 的输入和输出空间相同，但联合概率分布不同 $\Rightarrow {\mathcal{X}}_{\mathcal{S}}={\mathcal{X}}_{\mathcal{T}},{\mathcal{Y}}_{\mathcal{S}}={\mathcal{Y}}_{\mathcal{T}},p_s(x,y)\ne p_t(x,y)$.

4. 经典方法

DA 的目标是学习一个在 target domain 上效果好的分类器, 这等价于最小化在 target domain 上的expected risk, 用数学表示:
$$\begin{gathered} R_T(h)={\mathbb{E}}_{(x,y)\sim p_t(x,y)}[\ell (h(x),y)] \\ =\sum _{y\in Y}{\int }_X\ell (h(x),y)p_t(x,y)\frac{p_s(x,y)}{p_s(x,y)}dx \\ =\sum _{y\in Y}{\int }_X\ell (h(x),y)p_s(x,y)\frac{p_t(x,y)}{p_s(x,y)}dx \\ ={\mathbb{E}}_{(x,y)\sim p_s(x,y)}[\frac{p_t(x,y)}{p_s(x,y)}\ell (h(x),y)] \end{gathered}$$
这就可以与 source 建立联系, 且当设定为 covariate shift 时 [ $p_s(x)\ne p_t(x),p_s(y|x)=p_t(y|x)$]:
$$\begin{gathered} R_T(h)={\mathbb{E}}_{(x,y)\sim p_s(x,y)}[\frac{p_t(x)p_t(y|x)}{p_s(x)p_s(y|x)}\ell (h(x),y)] \\ ={\mathbb{E}}_{(x,y)\sim p_s(x,y)}[\frac{p_t(x)}{p_s(x)}\ell (h(x),y)] \end{gathered}$$
当设定为 prior shift 时 [$p_s(x|y)=p_t(x|y),p_s(y)\ne p_t(y)$]:
$$\begin{gathered} R_T(h)={\mathbb{E}}_{(x,y)\sim p_s(x,y)}[\frac{p_t(y)p_t(x|y)}{p_s(y)p_s(x|y)}\ell (h(x),y)] \\ ={\mathbb{E}}_{(x,y)\sim p_s(x,y)}[\frac{p_t(y)}{p_s(y)}\ell (h(x),y)] \end{gathered}$$
其中 $w(x)=\frac{p_t(x)}{p_s(x)}$ 被称为 importance weight 或 re-weighting factor, $w(y)=\frac{p_t(y)}{p_s(y)}$ 被称为 class weight.

所以很多早期经典论文都是从估计$w(x)$角度出发, 主要思路是寻找一个合适的$w(x)$ 使得 re-weighted source dist. 与 target dist. 之间的差距最小化, 这种方法称为 Density Ratio Estimation (DRE), 可以读以下论文:

• KMM - NeurIPS 2006
• KLIEP - NeurIPS 2007

还有很多方法从 source 和 target 的子空间进行研究 (GFK, SA, SDA), 随着神经网络的流行, 又有一些文章用 DNNs 学习 source 和 target 之间的关系 (DDC, DAN, DANN, DeepCoral, DRCN, CoGAN), 多为基于GAN的模型.

5. 常用数据集

1. Office-Home: https://arxiv.org/abs/1706.07522
2. VLSC: https://openaccess.thecvf.com/content_iccv_2013/papers/Fang_Unbiased_Metric_Learning_2013_ICCV_paper.pdf
3. DomainNet: https://ai.bu.edu/M3SDA/
4. RMNIST: https://arxiv.org/abs/1508.07680
5. CMNIST: https://arxiv.org/abs/1907.02893
6. PACS: https://arxiv.org/abs/1710.03077
7. Terra Incognita: https://arxiv.org/abs/1807.04975

这篇关于Domain Adaptation 相关介绍的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---