本文主要是介绍gdal平面几何空间关系，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！
关于平面几何的空间关系判定，gdal提供了8个函数，分别是：Intersects（相交），Equals（相等），Disjoint（不相交），Touches（接触），Crosses（交叉），Within（被包含），Contains（包含），Overlaps（重叠）。关于几种空间关系的概念，网上有许多权威解释，此处不做解释说明。本文仅研究gdal如何判定平面几何的空间关系。
面与面 
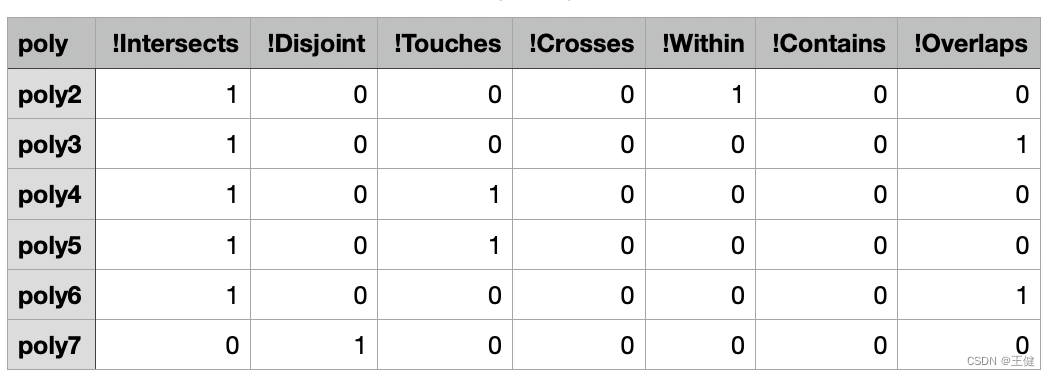
上图给出了一组多边形poly1~poly7，通过gdal判定poly1和其他几个多边形的空间关系，可以得到下面两张表（OP表示poly1.OP(poly*)，!OP表示poly*OP（poly1））：
线与面
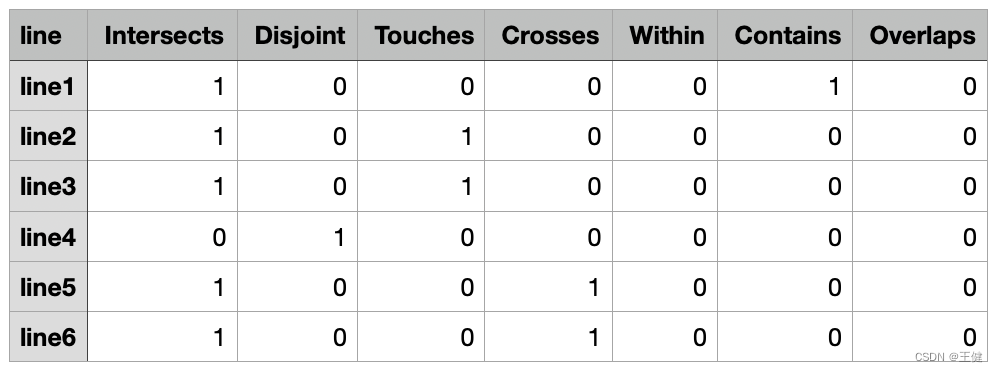
上图给出了一个多边形poly和一组线段line1~line6，通过gdal计算poly和line1~line6的空间关系，可以的到西面两张表（OP表示poly.OP(line*)，!OP表示line*OP（poly））：
点与面
上图给出了一个多边形poly和一组点F，C，G，通过gdal计算poly和F，C，F的空间关系，得出下面两张表（OP表示poly.OP(point*)，!OP表示line*OP（poly）)：
线与线
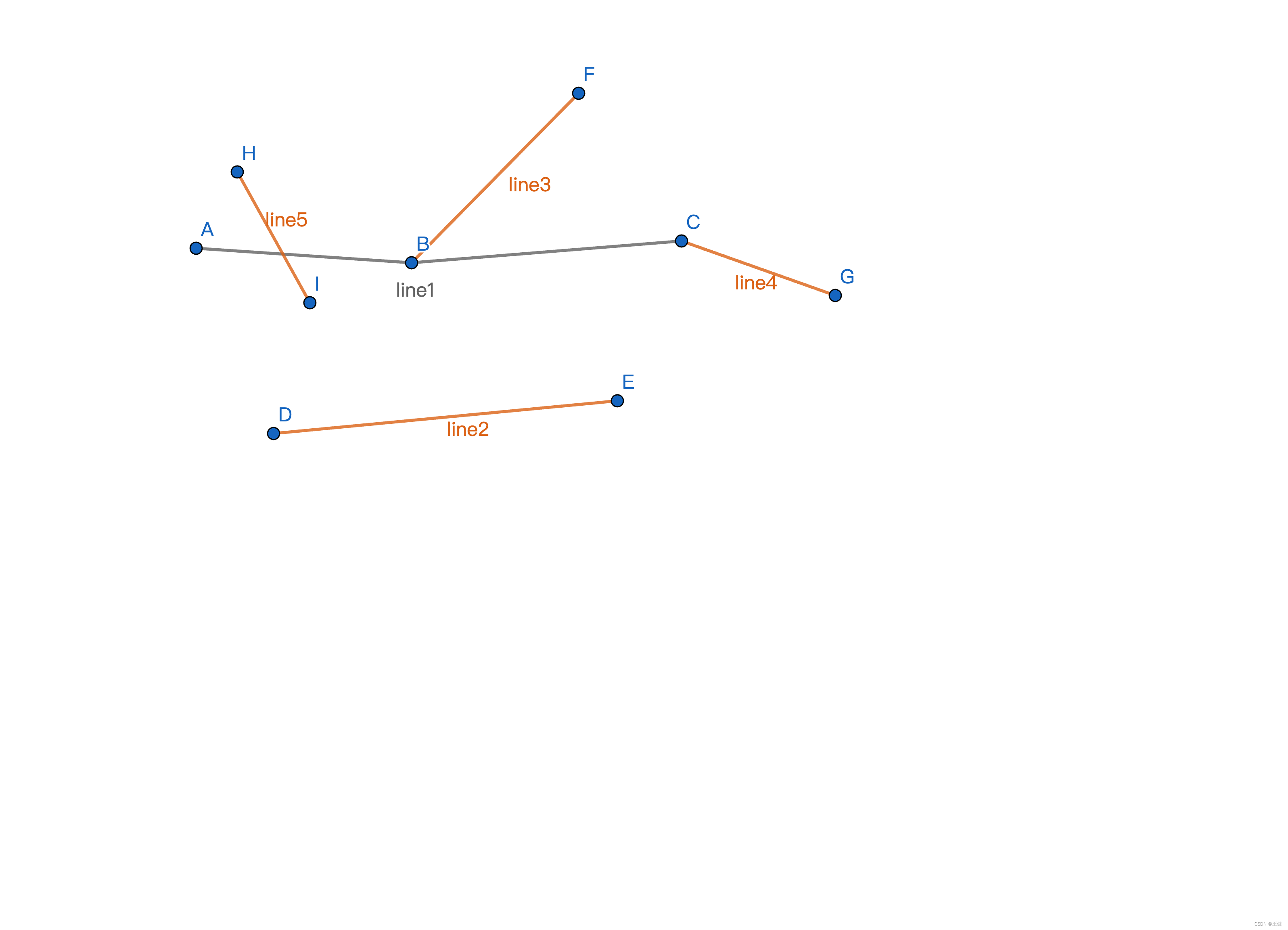
上图给出了一组线line1~line5，通过gdal计算line1和其他线line2~line5的空间关系，得出下面两张表（OP表示line1.OP(line*)，!OP表示line*OP（line）)：
点与线
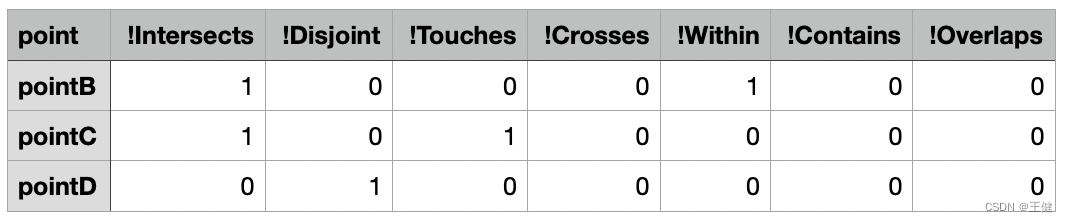
上图给出了一条线line和三个点B、C、D，通过gdal计算line和点B、C、D的空间关系，得出下面两张表（OP表示line.OP(point*)，!OP表示point*OP（line）)： 
由上面的表可以得出下面的结论：
-
Intersects和Disjoint两种空间关系互斥，两个几何图形要么Intersects，要么Disjoint，并且两种空间关系对于参与运算的双方是相互的，即如果A OP B成立，那么B OP A一定成立
-
Touches, Crosses，Within, Contains, Overlaps属于Intersects的特殊情况，Crosses、Intersects和Overlaps对于参与运算的双方是相互的，即如果A OP B成立，那么B OP A一定成立
-
Within和Contains两种位置关系不是相互的，即如果A OP B成立，那么B OP A一定不成立，但两种位置关系相反，即如果A Within B成立，那么B Contains A一定成立
-
面与面的空间关系包括 Intersects, Disjoint, Touches, Within, Contains, Overlaps
-
面与线的空间关系包括 Intersects, Disjoint, Touches, Crosses, Within, Contains
-
面与点的空间关系包括 Intersects, Disjoint, Touches, Within, Contains
-
线与线的空间关系包括 Intersects, Disjoint, Touches, Crosses, Within, Contains
-
线与点的空间关系包括 Intersects, Disjoint, Touches, Within, Contains
这篇关于gdal平面几何空间关系的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！
