【教学类-43-16】 20240106 推算5-9宫格数独可能出现的不重复题量（N宫格数独模板数量的推算）

本文主要是介绍【教学类-43-16】 20240106 推算5-9宫格数独可能出现的不重复题量（N宫格数独模板数量的推算），希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

作品展示：

通过对各种已有结果的人工推算，目前得到两个结论

一、阶乘==基本样式的数量【【123】【321】【231】【132】【312】【312】】6组

结论：阶乘等于出现的基本样式数量

以下N*N格会出现的最大排序数量（比如包含333222111这种不符合数独规律的元素）

'''
目的：测试N宫格可以生成多少组基本样式（乘阶）[1,2,3,4,5][5,4,3,2,1]}
作者：阿夏
时间：2024年1月6日19:00
'''import random
import math
from itertools import permutations# 宫格数gg=[1,2,3,4,5,6,7,8,9]
# gg=[5]
ggg=[]
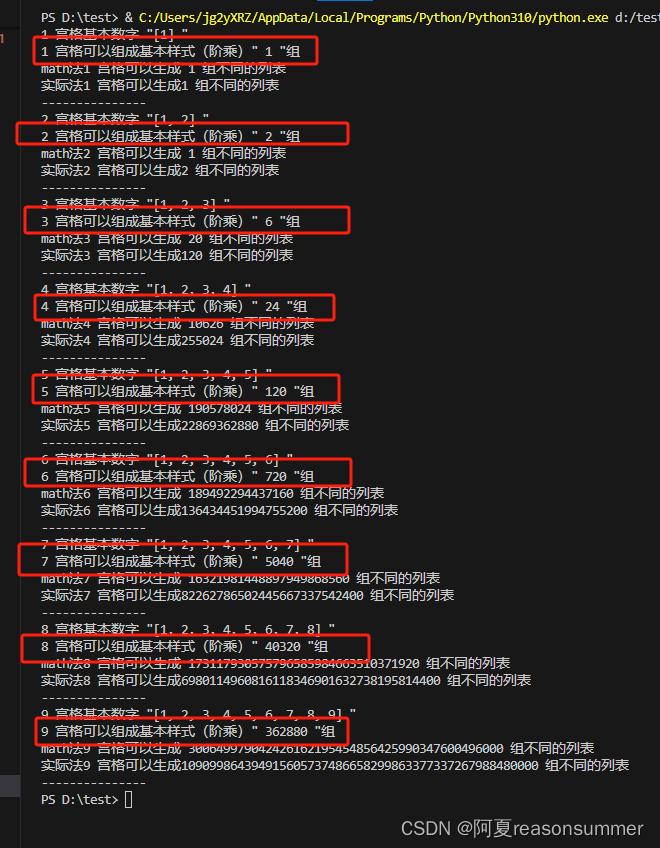
for hs in gg:n=[]for nu in range(1,hs+1):n.append(nu)# lst = ''.join(str(num) for num in n)# print(n)print('{} 宫格基本数字 "{} "'.format(hs,n))# 3宫格，基础数字是'123'# 123中间随机抽取3个，不同的3个数字排序方法permutations_list = list(permutations(n))numbers = [list(permutation) for permutation in permutations_list]# numbers = ''.join(str(num) for num in number)# print(numbers)print('{} 宫格可以组成基本样式（阶乘）" {} "组'.format(hs,len(numbers)))# [[1, 2, 3], [1, 3, 2], [2, 1, 3], [2, 3, 1], [3, 1, 2], [3, 2, 1]]# 6种组合# math生成可能的数量combinations = math.comb(len(numbers), hs)print("math法{} 宫格可以生成 {} 组不同的列表".format(hs ,combinations))# 在原有基础上乘上基本样式组的数量，如宫格基本样式是6组【123】【132】【213】【231】【312】【321】，通过互相交叉选取3个为一组，会有20种可能# 最后需要20*6=120，才是最大的生成数量。因此math计算后，还要乘以基本样式数量print("实际法{} 宫格可以生成{} 组不同的列表".format(hs ,combinations*len(numbers)))print('---------------')# 1 宫格基本数字 "[1] "
# 1 宫格可以组成基本样式（阶乘）" 1 "组       
# math法1 宫格可以生成 1 组不同的列表
# 实际法1 宫格可以生成1 组不同的列表
# ---------------
# 2 宫格基本数字 "[1, 2] "
# 2 宫格可以组成基本样式（阶乘）" 2 "组       
# math法2 宫格可以生成 1 组不同的列表
# 实际法2 宫格可以生成2 组不同的列表
# ---------------
# 3 宫格基本数字 "[1, 2, 3] "
# 3 宫格可以组成基本样式（阶乘）" 6 "组       
# math法3 宫格可以生成 20 组不同的列表        
# 实际法3 宫格可以生成120 组不同的列表        
# ---------------
# 4 宫格基本数字 "[1, 2, 3, 4] "
# 4 宫格可以组成基本样式（阶乘）" 24 "组      
# math法4 宫格可以生成 10626 组不同的列表     
# 实际法4 宫格可以生成255024 组不同的列表     
# ---------------
# 5 宫格基本数字 "[1, 2, 3, 4, 5] "
# 5 宫格可以组成基本样式（阶乘）" 120 "组     
# math法5 宫格可以生成 190578024 组不同的列表 
# 实际法5 宫格可以生成22869362880 组不同的列表
# ---------------
# 6 宫格基本数字 "[1, 2, 3, 4, 5, 6] "        
# 6 宫格可以组成基本样式（阶乘）" 720 "组     
# math法6 宫格可以生成 189492294437160 组不同的列表
# 实际法6 宫格可以生成136434451994755200 组不同的列表
# ---------------
# 7 宫格基本数字 "[1, 2, 3, 4, 5, 6, 7] "
# 7 宫格可以组成基本样式（阶乘）" 5040 "组
# math法7 宫格可以生成 16321981448897949868560 组不同的列表
# 实际法7 宫格可以生成82262786502445667337542400 组不同的列表
# ---------------
# 8 宫格基本数字 "[1, 2, 3, 4, 5, 6, 7, 8] "
# 8 宫格可以组成基本样式（阶乘）" 40320 "组
# math法8 宫格可以生成 173117930575796585984663510371920 组不同的列表
# 实际法8 宫格可以生成6980114960816118346901632738195814400 组不同的列表
# ---------------
# 9 宫格基本数字 "[1, 2, 3, 4, 5, 6, 7, 8, 9] "
# 9 宫格可以组成基本样式（阶乘）" 362880 "组
# math法9 宫格可以生成 300649979042426162195454856425990347600496000 组不同的列表
# 实际法9 宫格可以生成109099864394915605737486658299863377337267988480000 组不同的列表
# ---------------

二、用“阶乘结果”倒推，预测5-9宫格数独的不重复最大样式数量

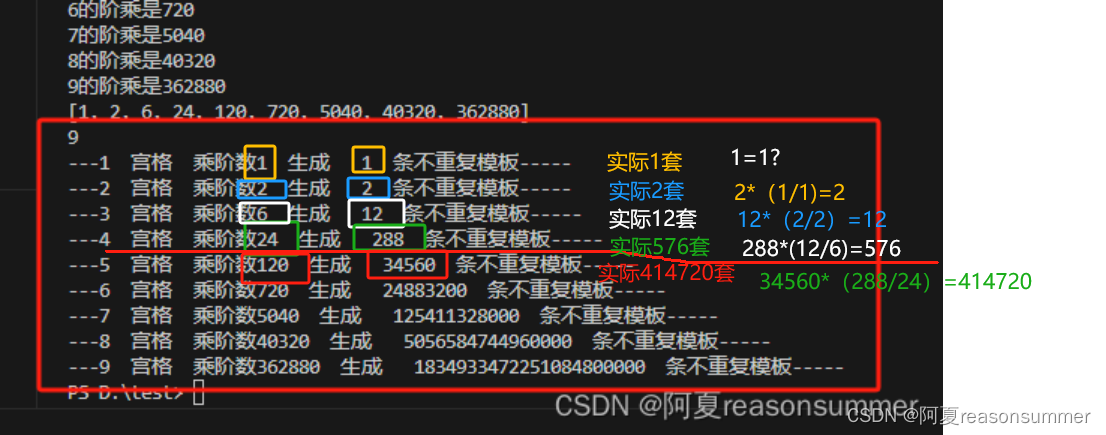我发现4宫格限制条件后，实际出现576套不重复模板，比阶乘测试的不重复模板288，正好是2倍。288*2=576，而这个2倍恰好是“3宫格中，不重复模板12条和阶乘6的除法结果。（前一条的除差）

用这个思路推算了1-4宫格，发现1宫格无法找前面一条的除法结果，但2宫格、3宫格、4宫格，都是符合这个规律。

------------------------------------------------------------------------------------------------------------

手动推算了5宫格的不重复模板数量

5宫格的阶乘推算不重复模板数量*（4宫格的阶乘模板数/4宫格的阶乘数）=预估数量

                 34460                         *              （288   /    24）                       =414720

代码推算5-9宫格数独题符合标准的不重复题目数量

'''
目的：测试N宫格可以生成多少不重复的数独题，从576=288*12/2推测
作者：阿夏
时间：2024年1月6日19:00
'''import random
import math
from itertools import permutations# 宫格数P=[]
Q=[]
R=[]hsall=[]
for i in range(1,10):    # 1-9宫格hsall.append(i)# 计算1-9各自的乘阶  jc=[]for hs in hsall:    j = math.factorial(hs)print('{}的阶乘是{}'.format(hs,j))jc.append(j)
print(jc)
# [1, 2, 6, 24, 120, 720, 5040, 40320, 362880]
print(len(jc))
# jc bs=[]
ds=[]result = []
product = 1
for num in range(len(jc)):product *= jc[num]c=int(product/jc[num])    # 除法结果，倍数# print(c)print('---{}  宫格  乘阶数{}  生成   {}  条不重复模板,除法结果是 {}-----'.format(hsall[num],jc[num],product,c))# 除法的结果（倍数）做成列表bs.append(c)# 阶乘推算的不重复模板数量ds.append(product)
print(bs)
# [1, 1, 2, 12, 288, 34560, 24883200, 125411328000, 5056584744960000]
print(ds)
# [1, 2, 12, 288, 34560, 24883200, 125411328000, 5056584744960000, 1834933472251084800000]# 因为1宫格无法找到0宫格的生成数量，所以bs前面再加1
bs.insert(0,1)
print(bs)
# [1, 1, 1, 2, 12, 288, 34560, 24883200, 125411328000, 5056584744960000]# 推算结果
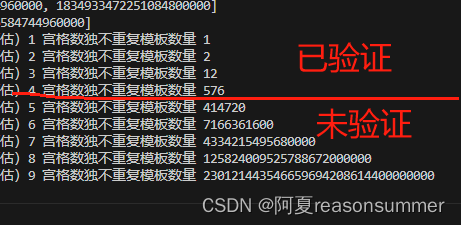
for o in range(len(ds)):print('阶乘推算不重复数量乘以“前宫格除法结果” 最大不重复数量（预估）{} 宫格数独不重复模板数量 {} '.format(o+1,int(ds[o])*int(bs[o])))# 阶乘推算不重复数量乘以“前宫格除法结果” 最大不重复数量（预估）1 宫格数独不重复模板数量 1
# 阶乘推算不重复数量乘以“前宫格除法结果” 最大不重复数量（预估）2 宫格数独不重复模板数量 2
# 阶乘推算不重复数量乘以“前宫格除法结果” 最大不重复数量（预估）3 宫格数独不重复模板数量 12
# 阶乘推算不重复数量乘以“前宫格除法结果” 最大不重复数量（预估）4 宫格数独不重复模板数量 576
# 阶乘推算不重复数量乘以“前宫格除法结果” 最大不重复数量（预估）5 宫格数独不重复模板数量 414720
# 阶乘推算不重复数量乘以“前宫格除法结果” 最大不重复数量（预估）6 宫格数独不重复模板数量 7166361600
# 阶乘推算不重复数量乘以“前宫格除法结果” 最大不重复数量（预估）7 宫格数独不重复模板数量 4334215495680000
# 阶乘推算不重复数量乘以“前宫格除法结果” 最大不重复数量（预估）8 宫格数独不重复模板数量 125824009525788672000000
# 阶乘推算不重复数量乘以“前宫格除法结果” 最大不重复数量（预估）9 宫格数独不重复模板数量 230121443546659694208614400000000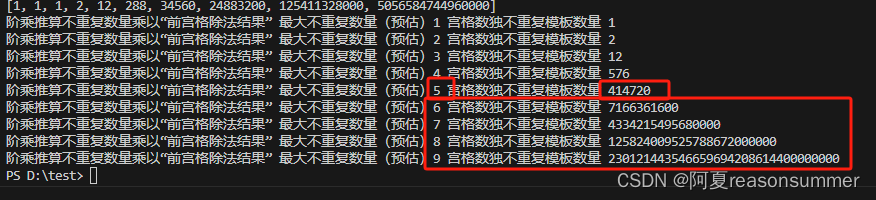

说明:

由于现在还无法用代码生成5宫格数独不重复题目，并排除重复（数据千亿次，电脑无法计算 MemoryError），获得正确的结果。

所以以上只是我根据已有的一些数字（3宫格数独12套、4宫格数独576套），按照一定规律推算出来的。不保证正确性。

最后把所有参数都写在一起print

'''
目的：测试N宫格可以生成多少不重复的数独题，从576=288*12/2推测
作者：阿夏
时间：2024年1月6日19:00
'''import random
import math
from itertools import permutations# 宫格数P=[]
Q=[]
R=[]hsall=[]
for i in range(1,10):    # 1-9宫格hsall.append(i)# 计算1-9各自的乘阶  jc=[]for hs in hsall:    j = math.factorial(hs)print('{}的阶乘是{}'.format(hs,j))jc.append(j)
print(jc)
# [1, 2, 6, 24, 120, 720, 5040, 40320, 362880]
print(len(jc))
# jc bs=[]
ds=[]
jcs=[]
jcmb=[]result = []
product = 1
for num in range(len(jc)):product *= jc[num]c=int(product/jc[num])    # 除法结果，倍数# print(c)print('---{}  宫格  乘阶数{}  生成   {}  条不重复模板,除法结果是 {}-----'.format(hsall[num],jc[num],product,c))jcs.append(jc[num])jcmb.append(product)# 除法的结果（倍数）做成列表bs.append(c)# 阶乘推算的不重复模板数量ds.append(product)
print(bs)
print(jcs)
# [1, 1, 2, 12, 288, 34560, 24883200, 125411328000, 5056584744960000]
print(ds)
# [1, 2, 12, 288, 34560, 24883200, 125411328000, 5056584744960000, 1834933472251084800000]# 因为1宫格无法找到0宫格的生成数量，所以bs前面再加1
bs.insert(0,1)
print(bs)
# [1, 1, 1, 2, 12, 288, 34560, 24883200, 125411328000, 5056584744960000]print('阶乘推算不重复数量乘以“前宫格除法结果” 最大不重复数量（预估）')
print('-----------------------------------')
# 推算结果
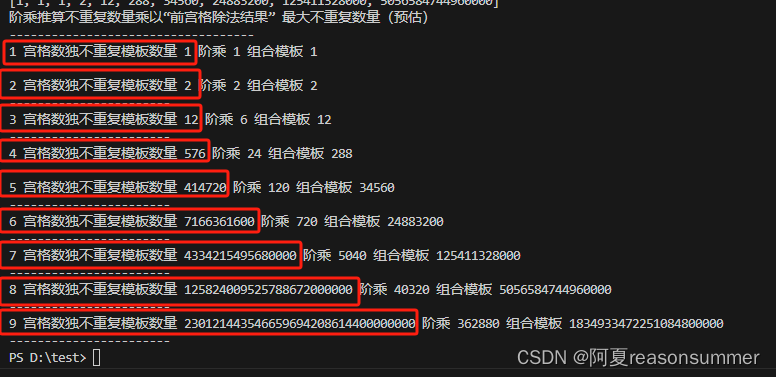
for o in range(len(ds)):print('{} 宫格数独不重复模板数量 {} 阶乘 {} 组合模板 {}  '.format(o+1, int(ds[o])*int(bs[o]),jcs[o],jcmb[o]))print('-----------------------')# 阶乘推算不重复数量乘以“前宫格除法结果” 最大不重复数量（预估）1 宫格数独不重复模板数量 1
# 阶乘推算不重复数量乘以“前宫格除法结果” 最大不重复数量（预估）2 宫格数独不重复模板数量 2
# 阶乘推算不重复数量乘以“前宫格除法结果” 最大不重复数量（预估）3 宫格数独不重复模板数量 12
# 阶乘推算不重复数量乘以“前宫格除法结果” 最大不重复数量（预估）4 宫格数独不重复模板数量 576
# 阶乘推算不重复数量乘以“前宫格除法结果” 最大不重复数量（预估）5 宫格数独不重复模板数量 414720
# 阶乘推算不重复数量乘以“前宫格除法结果” 最大不重复数量（预估）6 宫格数独不重复模板数量 7166361600
# 阶乘推算不重复数量乘以“前宫格除法结果” 最大不重复数量（预估）7 宫格数独不重复模板数量 4334215495680000
# 阶乘推算不重复数量乘以“前宫格除法结果” 最大不重复数量（预估）8 宫格数独不重复模板数量 125824009525788672000000
# 阶乘推算不重复数量乘以“前宫格除法结果” 最大不重复数量（预估）9 宫格数独不重复模板数量 230121443546659694208614400000000# 阶乘推算不重复数量乘以“前宫格除法结果” 最大不重复数量（预估）
# -----------------------------------
# 1 宫格数独不重复模板数量 1 阶乘 1 组合模板 1
# -----------------------
# 2 宫格数独不重复模板数量 2 阶乘 2 组合模板 2
# -----------------------
# 3 宫格数独不重复模板数量 12 阶乘 6 组合模板 12
# -----------------------
# 4 宫格数独不重复模板数量 576 阶乘 24 组合模板 288
# -----------------------
# 5 宫格数独不重复模板数量 414720 阶乘 120 组合模板 34560
# -----------------------
# 6 宫格数独不重复模板数量 7166361600 阶乘 720 组合模板 24883200
# -----------------------
# 7 宫格数独不重复模板数量 4334215495680000 阶乘 5040 组合模板 125411328000
# -----------------------
# 8 宫格数独不重复模板数量 125824009525788672000000 阶乘 40320 组合模板 5056584744960000
# -----------------------
# 9 宫格数独不重复模板数量 230121443546659694208614400000000 阶乘 362880 组合模板 1834933472251084800000
-----------------------

作为学美术专业的老师，我只有初中数学水平，o(╥﹏╥)o，

很希望有专业的编程员能提供经过验证的5宫格数独不重复模板题目数量 Thanks♪(･ω･)ﾉ

这篇关于【教学类-43-16】 20240106 推算5-9宫格数独可能出现的不重复题量（N宫格数独模板数量的推算）的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---