本文主要是介绍捍卫中华数学产权系列1.中国定理,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
知识产权是国家的文化命脉,是行业的生存根本,越是大国强国、越是头部行业越重视知识产权,他们在这上面可以说是锱铢必较、寸土不让。
古代中国数学是有许许多多知识产权的,但在不肖子孙的嚯嚯下,被强盗抢夺得寥寥无几,而面对强盗行径,中国数学人的一贯表现是呆若木鸡不敢说一个不字。本人致力于恢复、重建中华数学体系,也最看重数学创新,因为只有拥有知识产权,才能实现拓土开疆、才能让强权俯首。我认为学术是有国界的,中国人的知识产权绝不准许以任何方式送给他国!我在研究欧系数学漏洞的过程中有过一些发现,这些发现所带来的知识产权永远为中国数学所有,未来它们将成为中华数学体系的组成部分。今天是第一篇:关于中国定理。
中国定理决定中华数学复兴
一、来历
1982年,我第一次接触调和放缩法“1+1/2+1/3+1/4+…+1/n+…=1+1/2+(1/3+1/4)+…+(1/2)^k>1+1/2+1/2+…+1/2+…” 就认为它错得不可接受!无论是“1+1/2+1/3+1/4+…+1/n+…=1+1/2+(1/3+1/4)+…+(1/2)^k”还是“1+1/2+1/3+…+1/n+…>1+1/2+1/2+…+1/2+…” 都赤裸裸地反数理不成立,我认为世间绝不存在这种颠倒黑白的“等式”和“不等式”,并与科任数学老师李德福发生争执,遭到他的严厉斥责批评,他说“调和放缩法是西方经典,经典不可质疑”。尽管老师的态度如此鲜明,我还是不服气,我认为我的智商是正常的,我一眼就能看出的“没有通项、反逻辑、反数理”错误,难道数学家看不见吗?“1+1/2+1/3+1/4=1+1/2+(1/3+1/4)”可以没有问题,但是“1+1/2+1/3+1/4+…+1/n+…=1+1/2+(1/3+1/4)+…+(1/2)^k”有天大的问题啊!
调和放缩法,欧洲人的逆天经典
1983年春夏之交,受中华谜题“老汉分羊”启示我发现了一个公式:任意自然数之无穷等比数列之和,等于该自然数减1的倒数,写作“Σ(1/n)^k=1/(n-1)”。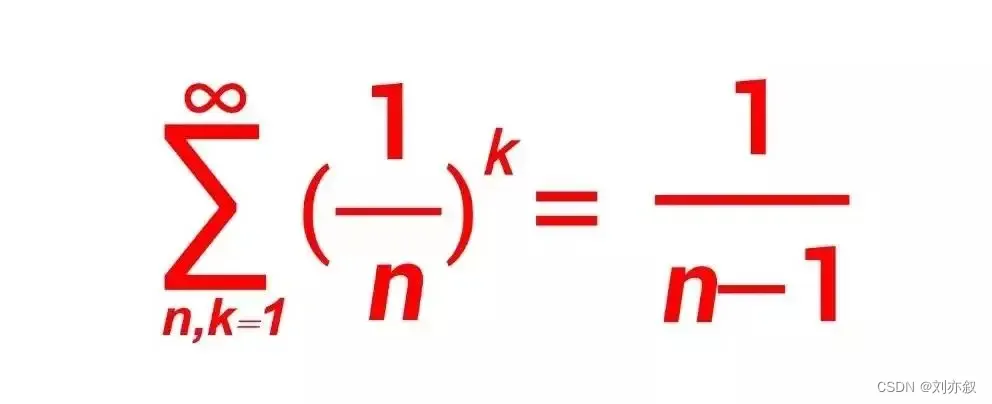
自然数之无穷等比数列之和,等于该数减1的倒数
为此写了“论文(叙述说明文)”,找时任数学老师周大德,他毫无兴趣;1984年秋天,我找到大连师专(现大连大学)数学系王麒麟老师,他认为很有价值推荐给校报发表,最终被系主任以“属于趣味数学,没有高数价值”挡了回来。后来我去了大连市内最著名的大连工学院(现大连理工大学)、大连海运学院(现大连海事大学),想寻求支持都没能如愿。之后我就将该话题束之高阁,直到2010年春节打扫卫生旧稿重现。
2013年我发现了“自然数集全覆盖通式”以后,坐实了调和级数绝对收敛,在随后多年与贴吧网友交流争论中意识到Σ(1/n)^k=1/(n-1)关乎中国数学“立国之战”,遂于2022年命名为中国定理。
二、证明方法。
中国定理的证明来自中华数学的消元法:1/2+1/4+…+1/2^k=(1-1/2)+(1/2-1/4)+…+{1/〔2^k-2^(k-1)-1/〔2^(k+1)-2^k}=1/(2-1)=1;1/3+1/9+…+1/3^k=(1/2-1/6)+(1/6-1/18)+…+{1/〔3^k-3^(k-1)-1/〔3^(k+1)-3^k}=1/(3-1)=1/2;1/5+1/25+…+1/5^k=(1/4-1/20)+(1/20-1/100)+…+{1/〔5^k-5^(k-1)-1/〔5^(k+1)-5^k}=1/(5-1)=1/4;……;1/n+1/n²+…+1/n^k=〔1/(n-1)-1/n(n-1)〕+〔1/n(n-1)-1/(n-1)*n²〕+…+{1/〔n^k-n^(k-1)-1/〔n^(k+1)-n^k}=1/(n-1),证毕!
消元法证明中国定理
三、广泛应用
中国定理功能强大用途广泛,解决问题得心应手、方法一目了然。
例一,团灭“22种Σ1/n发散证明方法”。
一步直算团灭欧系22种发散证明
中国定理对调和级数Σ1/n创造性地的实现了实算法(欧系使用的都是估算法、替代法、假冒法):1+1/2+1/3+1/4+…+1/n+…=1+(1/2+1/4+…+1/2^k)+(1/3+1/9+…+1/3^k)+…+(1/n+1/n²+…+1/n^k)=1+1+1/2+1/4+1/5+1/6+1/9+…+1/(n-1)【注:n≠(n+1)^(k+1)】,这是直算等式、是纯有理数整算,既不存在四舍五入误差也没有丝毫实值丢失,然而仅此一步,即能令“调和放缩法”失灵、让欧系数学祖祖辈辈积攒归纳的“22种Σ1/n发散证明方法”一并归谬(本人有26种证明调和级数收敛方法)!
例二、1/n级数求和公式鼻祖,利用中国定理可以推出众多1/n级数求和公式(如截图)。
例三、类Σ1/n问题求和通项公式。
例四、终结欧洲人0.999…≠1的扯皮难题。
四、中国定理与等比数列求和公式没有任何瓜葛。国内的欧系拥趸在这个问题上一直是胳膊肘往外拐,他们不断地叫嚣中国定理就是欧洲人的等比数列求和公式,试图让我把自己的发现让给他们的欧洲主人。
对这种声音,我总是据理力争
中国定理确实是等比数列求和,但从发现到推证、到应用都与欧洲人的等比数列求和公式都没有任何关联,等比数列求和公式也推导不出中国定理。有以下事实可以作证:①中国定理针对1/n无穷求和,等比求和公式用于任意等比有限求和;②等比求和公式如果能推导出中国定理,Σ1/n早就不会发散了;③无论欧洲典籍还是欧系拥趸从来没有出现过、使用过Σ(1/n)^k=1/(n-1)这个表达式;④我面对面接触过的专家学者没有哪个把中国定理与等比数列求和公式画过等号。
以上说明的目的就是:中国定理自始至终与欧洲人的等比数列求和公式没有关联,它的知识产权属于中国数学!假如有一天中国定理面对着欧美的产权纠缠,中国人能不能齐心协力捍卫自己的知识权利?别说它彻头彻尾属于中国智慧,即便牵扯到了欧系,中国人都应该据理力争,这是主权和原则问题!
这篇关于捍卫中华数学产权系列1.中国定理的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!







