本文主要是介绍sql实现均衡度计算(洛伦兹曲线,基尼系数),希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
1.基本介绍
均衡度:使用洛伦兹曲线计算基尼系数,基尼系数代表均衡度,系数值越大证明越不均衡度,值约小证明越均衡。【例:拿贫富差距人口收入举例,将累计人口百分比作X轴,累计收入百分比作Y轴,绘制贫富差距洛伦兹曲线如下图,使用面积法计算:基尼系数=A面积/(A面积+B面积)】(这里基尼系数不会大于1,也不会小于零)。
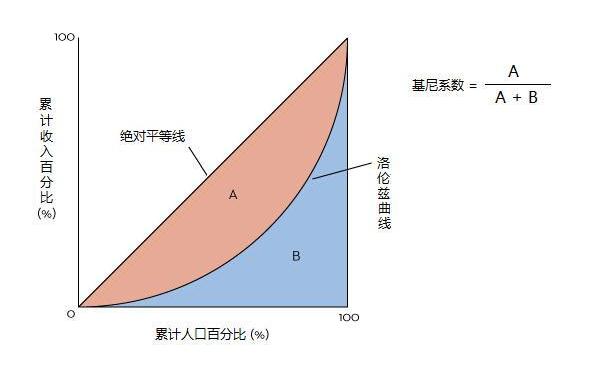
2.使用场景
(一)职权履行均衡度
假设某执法单位有职权2000项,按照职权触发次数由低到高排序,等分10份,及每200个职权分一个挡位,计算X轴(累计职权数百分比)、Y轴(累计职权触发次数百分比)如下表:
| 职权分档排序 | 每档职权触发次数 | X轴(职权累计百分比) | y轴(职权累计触发次数百分比) |
|---|---|---|---|
| 1-200 | 0 | 10% | 0 |
| 201-400 | 200 | 20% | 0.7% |
| 401-600 | 300 | 30% | 1.8% |
| 601-800 | 500 | 40% | 3.6% |
| 801-1000 | 550 | 50% | 5.6% |
| 1001-1200 | 999 | 60% | 9.3% |
| 1201-1400 | 1111 | 70% | 14% |
| 1401-1600 | 1765 | 80% | 20% |
| 1600-1800 | 1800 | 90% | 26% |
| 1800-2000 | 20000 | 100% | 100% |
绘制洛伦兹曲线如下图:
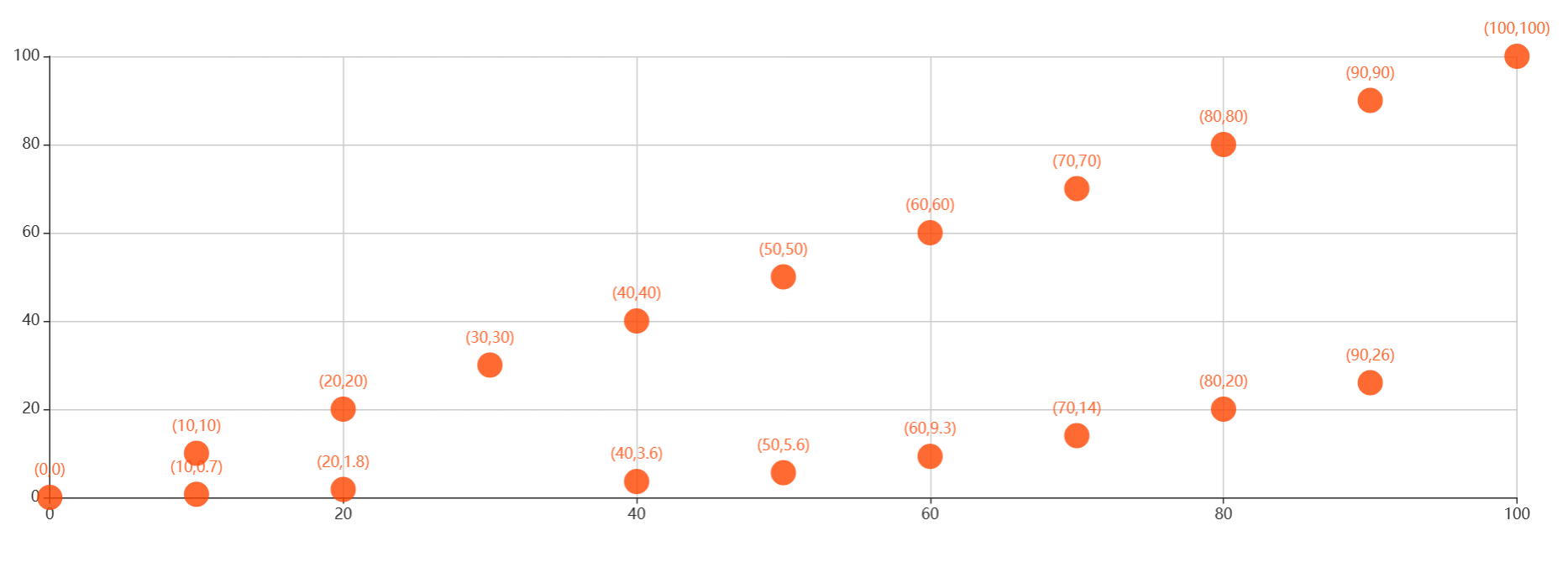
如图计算A、B区域面积得基尼系数为0.8,可得此单位处罚职权履行不均衡。
(二)案件月度分布均衡度
将某一执法单位每月案件量按照由小到大顺序排序,计算X轴(累计月份百分比)、Y轴(累计月案件量百分比)如下表:
| 月份 | 月检查量(万) | X轴(累计月份百分比) | Y轴(累计月检查量百分比) |
|---|---|---|---|
| 6月 | 1 | 8% | 2% |
| 11月 | 1 | 16% | 3% |
| 12月 | 1 | 25% | 5% |
| 1月 | 2 | 33% | 8.3% |
| 4月 | 4 | 42% | 15% |
| 2月 | 5 | 50% | 23.3% |
| 8月 | 5 | 58% | 31.6% |
| 3月 | 6 | 67% | 42% |
| 7月 | 8 | 75% | 55% |
| 5月 | 9 | 83% | 70% |
| 9月 | 9 | 92% | 85% |
| 10月 | 9 | 100% | 100% |
绘制洛伦兹曲线如下图:
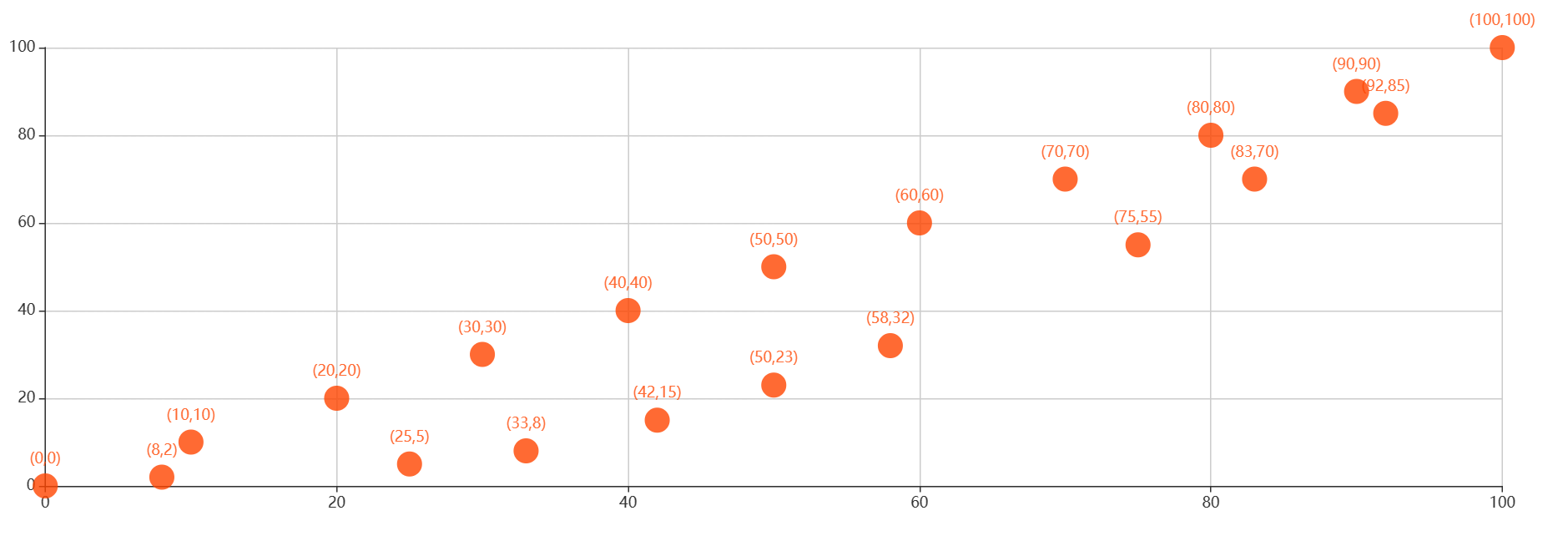
如图计算A、B区域面积得基尼系数为0.36,可得此单位检查月度分布较为均衡。
3.sql实现(函数)
计算均衡度(基尼系数)自定义函数(十等份计算,参数为查询到数据的sql语句的字符形式)
-- 根据批量数据进行分值切割从而计算均衡度
CREATE OR REPLACE FUNCTION JHD_JN(TABLENAME VARCHAR2) RETURN NUMBER
AS
T_COUNT NUMBER;
QUERY_SQL VARCHAR2(20000);
BEGIN
QUERY_SQL:='
-- 先计算得到各维度不同职权code的被触发数量
WITH POWER_ALL AS (' || TABLENAME || '
),
-- 对上方进行10等分切割得到每段的长度以及需要在第一段补充(0,0)的长度
-- eg: aa:73 bb:2 (每段73个但是第一段73-2个)
POWER_SUM AS (
SELECT CASE WHEN MOD((SELECT COUNT(1) FROM POWER_ALL), 10) > 0 THEN TRUNC(ROUND((SELECT COUNT(1) FROM POWER_ALL)/10, 1))+1 ELSE ROUND((SELECT COUNT(1) FROM POWER_ALL)/10) END aa,CASE WHEN MOD((SELECT COUNT(1) FROM POWER_ALL), 10) > 0 THEN10-MOD((SELECT COUNT(1) FROM POWER_ALL),10)ELSE 0END bb
FROM dual
),
-- 如果当前列数不满足等份便在开头增加上一步的余数个0,0
POWER_ALL_DATA AS (SELECT tb1.*,ROWNUM SORT FROM (SELECT ''0'' NAME,CASE WHEN (SELECT bb-aa FROM POWER_SUM) > 0 THEN 0ELSE NULLEND ALL_COUNT FROM (SELECT 1 FROM dual CONNECT BY LEVEL <= (SELECT bb FROM POWER_SUM))UNION ALLSELECT NAME,ALL_COUNT FROM POWER_ALL) tb1 WHERE tb1.ALL_COUNT IS NOT NULL
),
-- 先根据上方的aa对数据进行分割,假如有余数的话便先加上这个余数进行分割
POWER_LB1 AS (
SELECT tb1.ll-((SELECT aa FROM POWER_SUM)-1) s,tb1.ll e
FROM (SELECT LEVEL ll FROM dual CONNECT BY LEVEL < (SELECT COUNT(1) FROM POWER_ALL_DATA) + 1 + CASE WHEN (SELECT aa-bb FROM POWER_SUM) > 0 AND (SELECT bb FROM POWER_SUM) > 0 THEN (SELECT bb FROM POWER_SUM) ELSE 0 END
) tb1 WHERE MOD(tb1.ll, (SELECT aa FROM POWER_SUM)) = 0
),
-- 如果有余数的话再次进行处理,从而实现如果有余数的话将第一段减少
POWER_LB AS (
SELECT CASE WHEN (SELECT aa-bb FROM POWER_SUM) > 0 AND (SELECT bb FROM POWER_SUM) > 0 AND s != 1 THEN s - (SELECT bb FROM POWER_SUM)ELSE sEND s,CASE WHEN (SELECT aa-bb FROM POWER_SUM) > 0 AND (SELECT bb FROM POWER_SUM) > 0 THEN e - (SELECT bb FROM POWER_SUM)ELSE eEND e,ROWNUM*10 r
FROM POWER_LB1
),
-- 获取x和y轴数据(包含原点一共11个)
POWER_RESULT AS (
SELECT tb1.*,ROWNUM so FROM (SELECT 0 bfb,0 r FROM dual
UNION
SELECT CASE WHEN (SELECT SUM(ALL_COUNT) FROM POWER_ALL_DATA) = 0 THEN 0ELSE ROUND((SELECT SUM(ALL_COUNT)*100 FROM POWER_ALL_DATA WHERE SORT <= tb1.e)/(SELECT SUM(ALL_COUNT) FROM POWER_ALL_DATA),5)END bfb,rFROM POWER_LB tb1
) tb1 ORDER BY r
),
-- 计算面积一个三角形,九个梯形的和
POWER_DOWN_AREA AS (
SELECT SUM(jhd) DOWN_AREA FROM (SELECT CASE -- 三角形面积WHEN tb1.r < 1 THEN (SELECT ROUND(bfb*r/2 , 2)FROM POWER_RESULT WHERE so = 2)WHEN tb1.r = 11 THEN 0-- 九个梯形面积ELSE ROUND((tb1.bfb+(SELECT bfb FROM POWER_RESULT WHERE so = tb1.so + 1))*((SELECT r FROM POWER_RESULT WHERE so = tb1.so + 1) - tb1.r)/2,2)END jhd,tb1.*FROM POWER_RESULT tb1
))
-- 基尼系数(如果参数查询无数据则返回1,基尼系数最大为1。如果总面积为0则设置基尼系统为1)
-- 返回结果为百分数 eg:0.3 返回30
SELECT CASE WHEN ROUND(bfb*r/2, 2) = 0 THEN 100ELSE--NVL(ROUND(bfb*r/2, 2) - (SELECT * FROM POWER_DOWN_AREA),100)--ROUND(bfb*r/2, 2)NVL(ROUND((ROUND(bfb*r/2, 2) - (SELECT * FROM POWER_DOWN_AREA))/ROUND(bfb*r/2, 2),2),1)*100END AREA
FROM (SELECT * FROM POWER_RESULT ORDER BY SO DESC) WHERE ROWNUM < 2';
EXECUTE IMMEDIATE QUERY_SQL INTO T_COUNT;
RETURN T_COUNT;
END JHD_JN;
-- 直接根据X,Y数组进行均衡度计算
CREATE OR REPLACE FUNCTION JHD_JN1(TABLENAME VARCHAR2) RETURN NUMBER
AS
T_COUNT NUMBER;
QUERY_SQL VARCHAR2(20000);
BEGIN
QUERY_SQL:='
WITH POWER_RESULT AS (
' || TABLENAME || '
),
POWER_DOWN_AREA AS (
SELECT SUM(jhd) DOWN_AREA FROM (SELECT CASE -- 三角形面积WHEN tb1.X < 1 THEN (SELECT ROUND(Y*X/2 , 2)FROM POWER_RESULT WHERE so = 2)WHEN tb1.X = (SELECT COUNT(1) FROM POWER_RESULT) THEN 0-- 多个梯形面积ELSE ROUND((tb1.Y+(SELECT Y FROM POWER_RESULT WHERE so = tb1.so + 1))*((SELECT X FROM POWER_RESULT WHERE so = tb1.so + 1) - tb1.X)/2,2)END jhd,tb1.*FROM POWER_RESULT tb1
))
-- 基尼系数(如果参数查询无数据则返回1,基尼系数最大为1。如果总面积为0则设置基尼系统为1)
-- 返回结果为百分数 eg:0.3 返回30
SELECT CASE WHEN ROUND(Y*X/2, 2) = 0 THEN 100ELSENVL(ROUND((ROUND(Y*X/2, 2) - (SELECT * FROM POWER_DOWN_AREA))/ROUND(Y*X/2, 2),2),1)*100END AREA
FROM (SELECT * FROM POWER_RESULT ORDER BY SO DESC) WHERE ROWNUM < 2';
EXECUTE IMMEDIATE QUERY_SQL INTO T_COUNT;
RETURN T_COUNT;
END JHD_JN1;这篇关于sql实现均衡度计算(洛伦兹曲线,基尼系数)的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!





