153. Find Minimum in Rotated Sorted Array 旋转数组的最小数字

本文主要是介绍153. Find Minimum in Rotated Sorted Array 旋转数组的最小数字，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

题目描述

把一个数组最开始的若干个元素搬到数组的末尾，我们称之为数组的旋转。输入一个非递减序列的一个旋转，输出旋转数组的最小元素。例如数组{3,4,5,1,2}为{1,2,3,4,5}的一个旋转，该数组的最小值为1。

解答

　　最直观的解法从头到尾遍历整个数组，找到最小元素。这个解法的时间复杂度是O(n)。
　　注意到，旋转之后的数组实际上可以划分为两个排序的子数组，且前面的子数组的元素都大于或者等于后面子数组的元素。
　　还注意到，最小元素恰好是这两个子数组的分界线。
　　与二分查找一样，我们使用两个指针分别指向数组的第一个元素和最后一个元素。按照题目规则，第一个元素应该大于或等于最后一个元素（不完全正确，特例后叙）。
　　接着我们可以找到位于数组中间的元素。如果该元素位于前面的递增子数组，那么它应该大于或等于第一个指针指向的元素。此时数组中最小的元素应该位于该元素的后面。我们可以把第一个指针指向该中间元素，缩小寻找范围。移动后的第一个指针仍然位于前面的递增子数组中。
　　同样的，如果位于中间的元素位于后面的递增子数组，那么它应该小于或者等于第二个指针指向的元素。此时该数组中最小元素应该位于改中间元素的前面。我们可以把第二个指针指向中间元素，这样也可以缩小寻找范围。移动之后的第二个指针仍然位于后面的递增子数组。
　　接下来，我们使用更新后的两个指针，进行新一轮的查找。
　　按照上述思路，第一个指针总是指向前面递增数组的元素，第二个指针总是指向后面递增数组的元素。最终，第一个指针指向前面子数组的最后一个元素，第二个指针指向后面子数组的第一个元素。也就是说他们会指向相邻的元素，而第二个指针指向数组中的最小元素。这就是循环的终止条件。
　　这里写图片描述

int minNumberInRotateArray(vector<int> rotateArray) {if(rotateArray.empty())return 0;int start = 0;int end = rotateArray.size() - 1;int middle = 0;while (rotateArray[start] >=rotateArray[end]){if (end - start == 1){middle = end;break;}middle = (start + end) / 2;if (rotateArray[middle] >= rotateArray[start])start = middle;else if (rotateArray[middle] <= rotateArray[end])end = middle;}return rotateArray[middle];}

根据题目可以知道，在旋转数组中，总是把递增排序数组前面若干个数字搬到数组的后面，因此第一个数字总是大于或者等于最后一个数字。但是，按照定义，存在特例：将排序数组的前面0个元素搬到后面，即排序数组本身，也是一个旋转数组。此时，数组的第一个数字就是最小元素，可以直接返回。因此最开始把middle初始为start。即一旦发现第一个元素小于最后一个元素，就直接返回。

　　但是，考虑start和end指向的元素相等的情况，在前面的代码中，当二者相等且与middle指向的元素也想等时，将middle赋值给了start，即认为最小元素位于中间元素的后面。一定是这样么？
　　举个栗子，数组{1，0，1，1，1}和{1，1，1，0，1}都可以看做递增排序数组{0，1，1，1，1}的旋转。
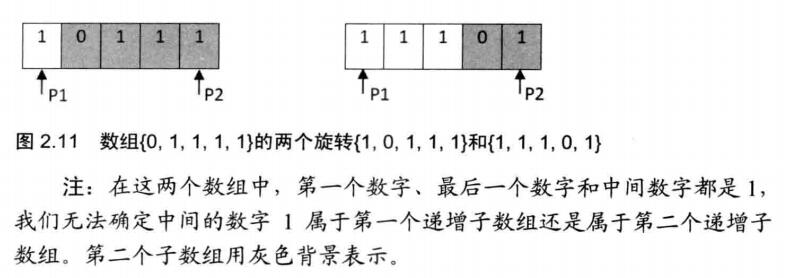
　　这里写图片描述
在这两种情况下，start、end和middle指针指向的数字都是1。在第一个数组中，中间数字位于后面的子数组；在第二个数组中，中间数字位于前面的子数组。因此，当两个指针指向的数字及它们中间的数字三者相等时，无法判断中间数字是位于前面的子数组还是后面的子数组，也就无法通过移动两个指针来缩小搜索范围。 此时，要采用顺序查找。

int minNumberInRotateArray(vector<int> rotateArray) {if(rotateArray.empty())return 0;int start = 0;int end = rotateArray.size() - 1;int middle = 0;while (rotateArray[start] >=rotateArray[end]){if (end - start == 1){middle = end;break;}middle = (start + end) / 2;if(rotateArray[start] == rotateArray[end] && rotateArray[middle] == rotateArray[start])return MinInOrder(rotateArray,start,end);if (rotateArray[middle] >= rotateArray[start])start = middle;else if (rotateArray[middle] <= rotateArray[end])end = middle;}return rotateArray[middle];}int MinInOrder(vector<int> rotateArray,int index1,int index2){int ret = rotateArray[index1];for(int i = index1+1;i<=index2;++i){if(ret >rotateArray[i])ret = rotateArray[i];}return ret;}

牛客网的oj有个问题，如果排序数组为空的情况下，直接返回0。这个bug。。。。。

Leetcode 讨论区的机智答案

对于这个问题，我们只会遇到三种情况
1. 数组中最左侧的值小于最右侧的值，这意味着数组没有旋转，例如[0,1,2,4,5,6,7]
2. 数组中间位置的数大于最左侧和最右侧的值，例如[4,5,6,7,0,1,2]
3. 数组中间位置的数小于最左侧和最右侧的值，例如[6,7,0,1,2,4,5]

从上面可以看到，如果我们遇到的是情况1，那么我们直接返回数组最左侧的值；如果我们遇到的是情况2，那么我们在数组的右半边寻找；如果我们遇到的是情况3，那么我们在数组的左半边寻找。

注意边界情况

class Solution {
public:int findMin(vector<int>& nums) {int start = 0;int end = nums.size()-1;while(start<end){if(nums[start] < nums[end])return nums[start];int mid = (start+end)/2;if(nums[mid] >= nums[start])start = mid+1;elseend = mid;}return nums[start]; }
};