【现代信号处理第六次作业】

2024-01-04 02:10
文章标签 作业 信号处理 现代 第六次

本文主要是介绍【现代信号处理第六次作业】，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

现代信号处理第六次作业

  • 1. 圆周卷积的定义如下
  • 2. DTFT和DFT变换
  • 3. 小波强制去噪
  • 4. 二次小波图像变换
  • 5. 心得和体会

1. 圆周卷积的定义如下

定义长度都为N的有限长序列 的循环卷积（圆周卷积）
x 1 ( n ) ⊗ x 2 ( n ) = ∑ i = 0 N − 1 x 1 ( i ) x 2 ( ( n − i ) ) N x_1(n)\otimes x_2(n)=\sum_{i=0}^{N-1}{x_1(i)x_2((n-i)})_N x1​(n)⊗x2​(n)=i=0∑N−1​x1​(i)x2​((n−i))N​
循环卷积所得序列的长度还是N，长度不变。
其中 表示对 进行圆周右移m运算，如长度为6的序列 ，其图形及圆周移位的图形如下图所示：
在这里插入图片描述

（a） （b） （c）
长度为N的序列 通过长度为L（ L<N）的系统 ，其响应可用圆周卷积定义为
y ( n ) = x 1 ( n ) ⊗ h 1 ( n ) = ∑ i = 0 N − 1 x 1 ( i ) h 1 ( ( n − i ) ) N y(n)=x_1(n)\otimes h_1(n)=\sum_{i=0}^{N-1}{x_1(i)h_1((n-i)})_N y(n)=x1​(n)⊗h1​(n)=i=0∑N−1​x1​(i)h1​((n−i))N​
其中 是将 的长度扩展到N（补零）得到。
如长度为4的有限长序列x(n)={1，1，1，1},通过系统h(n)={n=0,1,2}，则有 h 1 ( n ) = 1 ， 2 ， 0 ， 0 h_1(n)={1， 2，0，0} h1​(n)=1，2，0，0响应为
y ( 0 ) = x ( 0 ) h 1 ( ( 0 ) ) 4 + x 1 ( 1 ) h 1 ( ( − 1 ) ) 4 + x 1 ( 2 ) h 1 ( ( − 2 ) ) 4 + x ( 3 ) h 1 ( ( − 3 ) ) 3 y(0)=x(0)h_1((0))_4+x_1(1)h_1((-1))_4+x_1(2)h_1((-2))_4+x(3)h_1((-3))_3 y(0)=x(0)h1​((0))4​+x1​(1)h1​((−1))4​+x1​(2)h1​((−2))4​+x(3)h1​((−3))3​
= x 1 ( 0 ) h 1 ( 0 ) + x 1 ( 1 ) h 1 ( 3 ) + x 1 ( 2 ) h 1 ( 2 ) + x ( 3 ) h 1 ( 1 ) =x_1(0)h_1(0)+x_1(1)h_1(3)+x_1(2)h_1(2)+x(3)h_1(1) =x1​(0)h1​(0)+x1​(1)h1​(3)+x1​(2)h1​(2)+x(3)h1​(1)
y ( 1 ) = x ( 0 ) h 1 ( ( 1 ) ) 4 + x 1 ( 1 ) h 1 ( ( 0 ) ) 4 + x 1 ( 2 ) h 1 ( ( − 1 ) ) 4 + x ( 3 ) h 1 ( ( − 2 ) ) 3 y(1)=x(0)h_1((1))_4+x_1(1)h_1((0))_4+x_1(2)h_1((-1))_4+x(3)h_1((-2))_3 y(1)=x(0)h1​((1))4​+x1​(1)h1​((0))4​+x1​(2)h1​((−1))4​+x(3)h1​((−2))3​
= x 1 ( 0 ) h 1 ( 1 ) + x 1 ( 1 ) h 1 ( 0 ) + x 1 ( 2 ) h 1 ( 3 ) + x ( 3 ) h 1 ( 2 ) . . . . . =x_1(0)h_1(1)+x_1(1)h_1(0)+x_1(2)h_1(3)+x(3)h_1(2)\bigm...... =x1​(0)h1​(1)+x1​(1)h1​(0)+x1​(2)h1​(3)+x(3)h1​(2).....
参考我们上课讲到的卷积实现的算法完成下列问题
问题：序列 x ( n ) = c o s ( 0.2 π n ) x(n)=cos{(}0.2\pi n) x(n)=cos(0.2πn)，通过系统 h 1 ( n ) = 1 ， 2 ， 0 ， 0 h_1(n)={1， 2，0，0} h1​(n)=1，2，0，0 ；
（1）用matlab完成下列圆周卷积的结果（ 的长度取100）,并与matlab的cconv(x1,x2,N)函数结果进行比较。
（2）比较圆周卷积和线性卷积（conv普通卷积）所得到的结果，分析圆周卷积的优点。（20分）
解：（1）
代码：
定义圆周卷积函数circonvt

function y=circonvt(x1,x2,N) 
x_1=[x1 zeros(1,N-length(x1))]; 
h_1=[x2 zeros(1,N-length(x2))]; 
y1=conv(x_1,h_1);
z_1=[zeros(1,N) y1(1:(N-1))]; 
z_2=[y1((N+1):(2*N-1)) zeros(1,N)];
z=z_1(1:(2*N-1))+z_2(1:(2*N-1))+y1(1:(2*N-1)); 
y=z(10:N+10);
end

%% 1圆周卷积的定义如下
%（1）
clc;clear;
n=20;
t=0:99;
t1=0:n-1;
xn=cos(0.2*pi*t);
hn=[1,-2,2,-1,zeros(1,96)];
y1=circonvt(xn,hn,100);
y2=cconv(xn,hn,100);
hn=hn(1:n);
Y1=y1(1:n);
Y2=y2(1:n);
figure(1);
subplot(1,3,1);
stem(t,xn); ylabel ('hn'); xlabel ('t');title('xn原始信号'); grid on;
subplot(1,3,2);
stem(t1,Y1); ylabel ('Y1'); xlabel ('t');title('自定义圆周卷积circonvt'); grid on;
subplot(1,3,3);
stem(t1,Y2); ylabel ('Y2'); xlabel ('t');title('matlab圆周卷积cconv'); grid on;
hold on;
%%

如图1：
在这里插入图片描述
图1
对比上图可知，两种图像一致，说明函数构造正确。
（2）
代码：

%（2）
y3=conv(xn,hn);
Y3=y3(1:n);
figure(2);
subplot(1,3,1);
stem(t,xn); ylabel ('hn'); xlabel ('t');title('xn原始信号'); grid on;
subplot(1,3,2);
stem(t1,Y2); ylabel ('Y2'); xlabel ('t');title('matlab圆周卷积cconv'); grid on;
subplot(1,3,3);
stem(t1,Y3); ylabel ('Y3'); xlabel ('t');title('matlab线性卷积conv'); grid on;
%%

如图2：
在这里插入图片描述

图2
对比分析可得，圆周卷积是周期函数，线性卷积不是周期函数，线性卷积后面周期与圆周卷积一致。

2. DTFT和DFT变换

无限长序列 ，（1）画出其幅度谱；（2）将序列截取长度N=128的有限长序列，画出其DTFT频谱和DFT频谱。（3）例举计算机借助傅里叶变换分析信号频谱的步骤和方法，并指出会带来那些失真？（20分）
解：（1）
代码：
dfs函数

function[Xk]=dfs(xn,N)
n=0:N-1;
k=0:N-1;
WN=exp(-j*2*pi/N);
nk=n'*k;
Xk=(xn*WN.^nk)/N;
end

Idfs函数

function[xn]=Idfs(Xk,N)
n=0:N-1;
k=0:N-1;
WN=exp(j*2*pi/N);
nk=n'*k;
xn=(Xk*WN.^nk);
end

%% 2
% (1)
clc;clear;
n=0:0.01:2*pi;
x1n=(0.98).^n;
N = size(n,2);
Xk = dfs(x1n, N);
figure(3);
plot(n,abs(Xk));ylabel ('|Xk|'); xlabel ('n'); title('原序列的幅度谱'); %显示序列的幅度谱
hold on;
%%

如图3：
在这里插入图片描述

图3

（2）
代码：

%%
% (2)
n2 = 0:128;
n2 = n2*2*pi/128;
x128n=(0.98).^n2;
N2 = size(x128n,2);
X128k = dfs(x128n,N2);
k128 = 0:N2-1;
figure(4);
subplot(1,2,1);%2*2图形中的第一个
plot(k128,abs(X128k)); ylabel ('|X128k|'); xlabel ('k128');  title('128序列的DTFT频谱');
subplot(1,2,2);
stem(k128,abs(X128k)); ylabel ('|X128k|'); xlabel ('k128'); title('128序列的DFT频谱');
hold on;
%%

如图4：
在这里插入图片描述

图4
(3)
傅里叶变换分析信号频谱的步骤：先离散后傅里叶变换
方法：dfs /fft
由图4可知，无限长序列在截取后，其频谱会失真，此失真叫截取失真。截取长度越小失真越严重。无限长序列截短后，其频谱会产生失真，此失真叫截取失真。

3. 小波强制去噪

构造一个正弦信号 + 噪声，只采用matlab的dwt(x,’wname’)和idwt(ca1,cd1,‘db2’)函数完成小波强制去噪的仿真。其中wname分别采用db1和db2、小波去噪采用一次分解和二次分解情况，总共4个仿真结果，分析去噪前后的信噪比。（20分）
解：
代码：

%% 3
clc;clear
X = 10*sin(0:pi/100:6*pi);
Y = awgn(X,15,'measured');
sigPower = sum(abs(X).^2)/length(X)           %求出信号功率
noisePower=sum(abs(Y-X).^2)/length(Y-X)  %求出噪声功率
SNR=10*log10(sigPower/noisePower)          %由信噪比定义求出信噪比，单位为db
figure(5);
subplot(5,1,1);plot(Y);
xlabel('采样点'); ylabel('振幅');title(sprintf('原始信号,信噪比 %f',SNR));
% db1第一次分解
[ca1,cd1]=dwt(Y,'db1');
cd1=zeros(1,length(cd1));
X1=idwt(ca1,cd1,'db1');
X1=X1(1,1:601);
sigPower = sum(abs(X1).^2)/length(X1)           %求出信号功率
noisePower=sum(abs(X1-X).^2)/length(X1-X)  %求出噪声功率
SNR=10*log10(sigPower/noisePower)          %由信噪比定义求出信噪比，单位为db
subplot(5,1,2);plot(X1);
xlabel('采样点'); ylabel('振幅');title(sprintf('db1第一次分解,信噪比 %f',SNR));
% db1第二次分解
[ca2,cd2]=dwt(X1,'db1');
cd2=zeros(1,length(cd2));
X2=idwt(ca2,cd2,'db1');
X2=X2(1,1:601);
sigPower = sum(abs(X2).^2)/length(X2)           %求出信号功率
noisePower=sum(abs(X2-X).^2)/length(X2-X)  %求出噪声功率
SNR2=10*log10(sigPower/noisePower)          %由信噪比定义求出信噪比，单位为db
subplot(5,1,3);plot(X2);
xlabel('采样点'); ylabel('振幅');title(sprintf('db1第二次分解,信噪比 %f',SNR2));
% db2第一次分解
[ca3,cd3]=dwt(Y,'db2');
cd3=zeros(1,length(cd3));
X3=idwt(ca3,cd3,'db2');
X3=X3(1,1:601);
sigPower = sum(abs(X3).^2)/length(X3)           %求出信号功率
noisePower=sum(abs(X3-X).^2)/length(X3-X)  %求出噪声功率
SNR3=10*log10(sigPower/noisePower)          %由信噪比定义求出信噪比，单位为db
subplot(5,1,4);plot(X3);
xlabel('采样点'); ylabel('振幅');title(sprintf('db2第一次分解,信噪比 %f',SNR3));
% db2第二次分解
[ca4,cd4]=dwt(X3,'db2');
cd4=zeros(1,length(cd4));
X4=idwt(ca4,cd4,'db2');
X4=X4(1,1:601);
sigPower = sum(abs(X4).^2)/length(X4)           %求出信号功率
noisePower=sum(abs(X4-X).^2)/length(X4-X)  %求出噪声功率
SNR4=10*log10(sigPower/noisePower)          %由信噪比定义求出信噪比，单位为db
subplot(5,1,5);plot(X4);
xlabel('采样点'); ylabel('振幅');title(sprintf('db2第二次分解,信噪比 %f',SNR4));

如图5：
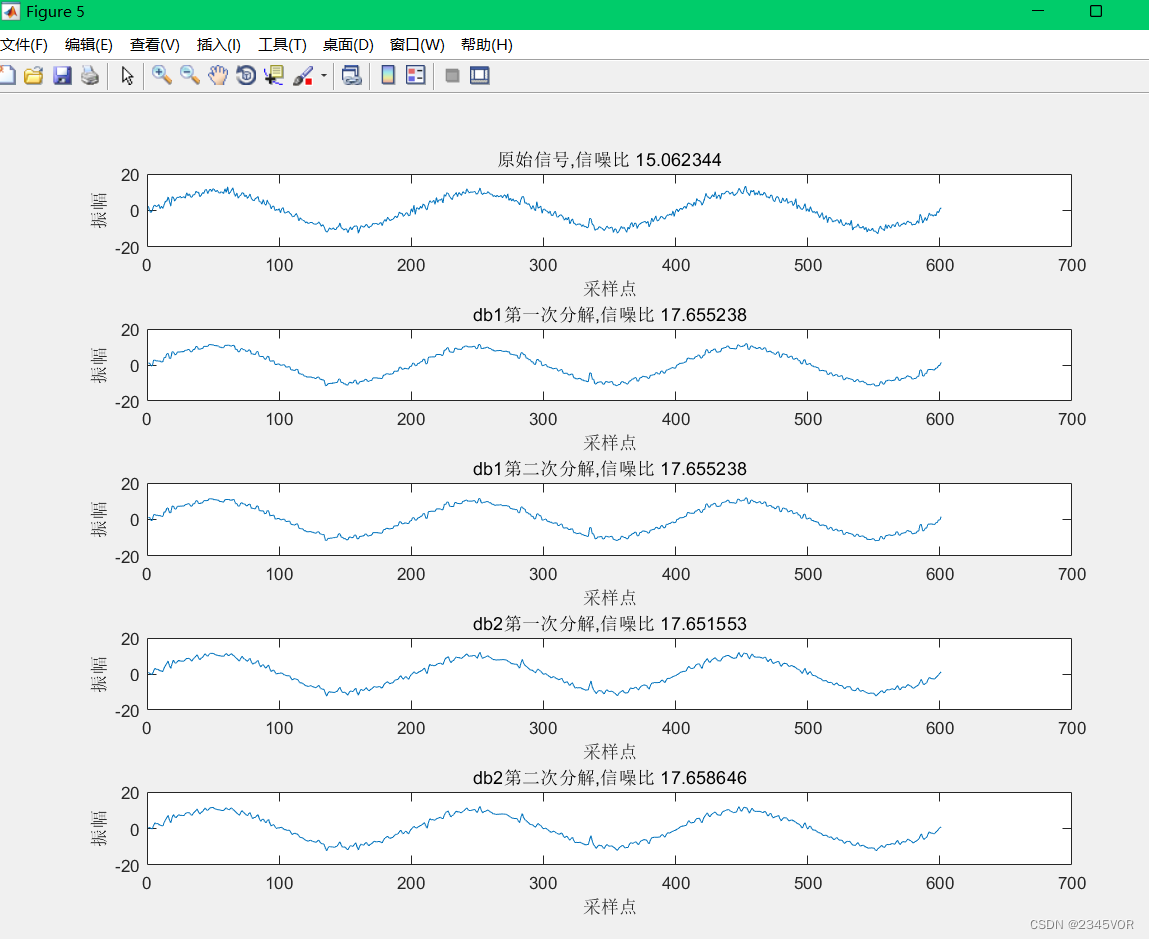
在这里插入图片描述

图5
对比前后图像可知，针对此模型型号强制去噪信噪比有了明显提高，db1比db2强制去噪明显。

4. 二次小波图像变换

用二次小波变换函数dwt2完成一幅图篇的2次小波变换，并用idwt2实现2次小波分解后的图像还原。（20分）
解：
代码：

%% 
% idwt2函数
% 功能：二维离散小波反变换
clc;clear;
load woman;
nbcol = size(map,1);%返回矩阵的行数和列数
[cA1,cH1,cV1,cD1]=dwt2(X,'db1');
cod_x=wcodemat(X,nbcol);%返回矩阵X的编码矩阵，nbcol为编码的最大值
cod_cA1=wcodemat(cA1,nbcol);
cod_cH1=wcodemat(cH1,nbcol);
cod_cV1=wcodemat(cV1,nbcol);
cod_cD1=wcodemat(cD1,nbcol);
dec2d=[cod_cA1,cod_cH1;cod_cV1,cod_cD1];
A0=idwt2(cA1,cH1,cV1,cD1,'db1');
figure(10);
subplot(2,2,1),imshow(X,[]);
title('原始图像');
subplot(2,2,2),imshow(dec2d,[])
title('二维离散小波分解后的图像');
subplot(2,2,3),imshow(X,[])
title('原始图像');
subplot(2,2,4),imshow(A0,[])
title('二维小波分解重构后的图像');
%%

如图6
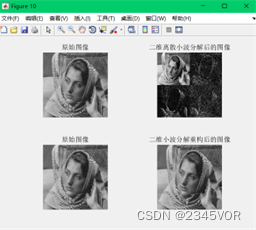
在这里插入图片描述
图6
test完整代码：

%% 1圆周卷积的定义如下
%（1）
clc;clear;
n=20;
t=0:99;
t1=0:n-1;
xn=cos(0.2*pi*t);
hn=[1,-2,2,-1,zeros(1,96)];
y1=circonvt(xn,hn,100);
y2=cconv(xn,hn,100);
hn=hn(1:n);
Y1=y1(1:n);
Y2=y2(1:n);
figure(1);
subplot(1,3,1);
stem(t,xn); ylabel ('hn'); xlabel ('t');title('xn原始信号'); grid on;
subplot(1,3,2);
stem(t1,Y1); ylabel ('Y1'); xlabel ('t');title('自定义圆周卷积circonvt'); grid on;
subplot(1,3,3);
stem(t1,Y2); ylabel ('Y2'); xlabel ('t');title('matlab圆周卷积cconv'); grid on;
hold on;
%(2)
y3=conv(xn,hn);
Y3=y3(1:n);
figure(2);
subplot(1,3,1);
stem(t,xn); ylabel ('hn'); xlabel ('t');title('xn原始信号'); grid on;
subplot(1,3,2);
stem(t1,Y2); ylabel ('Y2'); xlabel ('t');title('matlab圆周卷积cconv'); grid on;
subplot(1,3,3);
stem(t1,Y3); ylabel ('Y3'); xlabel ('t');title('matlab线性卷积conv'); grid on;%% 2
% (1)
clc;clear;
n=0:0.01:2*pi;
x1n=(0.98).^n;
N = size(n,2);
Xk = dfs(x1n, N);
figure(3);
plot(n,abs(Xk));ylabel ('|Xk|'); xlabel ('n'); title('原序列的幅度谱'); %显示序列的幅度谱
hold on;
% (2)
n2 = 0:128;
n2 = n2*2*pi/128;
x128n=(0.98).^n2;
N2 = size(x128n,2);
X128k = dfs(x128n,N2);
k128 = 0:N2-1;
figure(4);
subplot(1,2,1);%2*2图形中的第一个
plot(k128,abs(X128k)); ylabel ('|X128k|'); xlabel ('k128');  title('128序列的DTFT频谱');
subplot(1,2,2);
stem(k128,abs(X128k)); ylabel ('|X128k|'); xlabel ('k128'); title('128序列的DFT频谱');
hold on;%% 3
clc;clear
X = 10*sin(0:pi/100:6*pi);
Y = awgn(X,15,'measured');
sigPower = sum(abs(X).^2)/length(X)           %求出信号功率
noisePower=sum(abs(Y-X).^2)/length(Y-X)  %求出噪声功率
SNR=10*log10(sigPower/noisePower)          %由信噪比定义求出信噪比，单位为db
figure(5);
subplot(5,1,1);plot(Y);
xlabel('采样点'); ylabel('振幅');title(sprintf('原始信号,信噪比 %f',SNR));
% db1第一次分解
[ca1,cd1]=dwt(Y,'db1');
cd1=zeros(1,length(cd1));
X1=idwt(ca1,cd1,'db1');
X1=X1(1,1:601);
sigPower = sum(abs(X1).^2)/length(X1)           %求出信号功率
noisePower=sum(abs(X1-X).^2)/length(X1-X)  %求出噪声功率
SNR=10*log10(sigPower/noisePower)          %由信噪比定义求出信噪比，单位为db
subplot(5,1,2);plot(X1);
xlabel('采样点'); ylabel('振幅');title(sprintf('db1第一次分解,信噪比 %f',SNR));
% db1第二次分解
[ca2,cd2]=dwt(X1,'db1');
cd2=zeros(1,length(cd2));
X2=idwt(ca2,cd2,'db1');
X2=X2(1,1:601);
sigPower = sum(abs(X2).^2)/length(X2)           %求出信号功率
noisePower=sum(abs(X2-X).^2)/length(X2-X)  %求出噪声功率
SNR2=10*log10(sigPower/noisePower)          %由信噪比定义求出信噪比，单位为db
subplot(5,1,3);plot(X2);
xlabel('采样点'); ylabel('振幅');title(sprintf('db1第二次分解,信噪比 %f',SNR2));
% db2第一次分解
[ca3,cd3]=dwt(Y,'db2');
cd3=zeros(1,length(cd3));
X3=idwt(ca3,cd3,'db2');
X3=X3(1,1:601);
sigPower = sum(abs(X3).^2)/length(X3)           %求出信号功率
noisePower=sum(abs(X3-X).^2)/length(X3-X)  %求出噪声功率
SNR3=10*log10(sigPower/noisePower)          %由信噪比定义求出信噪比，单位为db
subplot(5,1,4);plot(X3);
xlabel('采样点'); ylabel('振幅');title(sprintf('db2第一次分解,信噪比 %f',SNR3));
% db2第二次分解
[ca4,cd4]=dwt(X3,'db2');
cd4=zeros(1,length(cd4));
X4=idwt(ca4,cd4,'db2');
X4=X4(1,1:601);
sigPower = sum(abs(X4).^2)/length(X4)           %求出信号功率
noisePower=sum(abs(X4-X).^2)/length(X4-X)  %求出噪声功率
SNR4=10*log10(sigPower/noisePower)          %由信噪比定义求出信噪比，单位为db
subplot(5,1,5);plot(X4);
xlabel('采样点'); ylabel('振幅');title(sprintf('db2第二次分解,信噪比 %f',SNR4));
%% 4 二次小波变换函数dwt2
% idwt2函数
% 功能：二维离散小波反变换
clc;clear;
load woman;
nbcol = size(map,1);%返回矩阵的行数和列数
[cA1,cH1,cV1,cD1]=dwt2(X,'db1');
cod_x=wcodemat(X,nbcol);%返回矩阵X的编码矩阵，nbcol为编码的最大值
cod_cA1=wcodemat(cA1,nbcol);
cod_cH1=wcodemat(cH1,nbcol);
cod_cV1=wcodemat(cV1,nbcol);
cod_cD1=wcodemat(cD1,nbcol);
dec2d=[cod_cA1,cod_cH1;cod_cV1,cod_cD1];
A0=idwt2(cA1,cH1,cV1,cD1,'db1');
figure(6);
subplot(2,2,1),imshow(X,[]);
title('原始图像');
subplot(2,2,2),imshow(dec2d,[])
title('二维离散小波分解后的图像');
subplot(2,2,3),imshow(X,[])
title('原始图像');
subplot(2,2,4),imshow(A0,[])
title('二维小波分解重构后的图像');

5. 心得和体会

分享学习本课程的心得和体会；并与自己的研究方向相联系，所学知识如何应用到今后的科研中（1000字左右）。

现代信号处理学习心得
首先非常感谢老师这八周来的激情演讲，让我们深刻领略到现代信号处理的魅力，无论我们来自何方，专业怎么样，老师从最基础的给我们一点一点的讲解，非常难得可贵的！
回望这八周的系统性学习，深刻感受到老师的数学素养，功底十分深厚，值得我们追随学习。首先从信号的采样讲起，了解到我们这个世界基本都是把无限序列进行有限离散化处理，然后再从中发现其规律和特点，以捕捉到最细微的本质。紧接着探索卷积的本质，从手撸代码一点一点教会我们理解他是怎样的思想以及背后的数学原理。虽然这个过程中出了许多小插曲，但老师还是克服万难。像我们展示了其中的奥妙。
随机数字信号处理是由多种学科知识交叉渗透形成的，在通信、雷达、语音处理、图象处理、声学、地震学、地质勘探、气象学、遥感、生物医学工程、核工程、航天工程等领域中都离不开随机数字信号处理。随着计算机技术的进步，随机数字信号处理技术得到飞速发展。本门课主要研究了随机数字信号处理的两个主要问题:滤波器设计和频谱分析。在数字信号处理中，滤波技术占有极其重要的地位。数字滤波是语音和图像处理、模式识别、频谱分析等应用中的一个基本处理算法。但在许多应用场合，常常要处理一些无法预知的信号、噪声或时变信号，如果采用具有固定滤波系数的数字滤波器则无法实现最优滤波。在这种情况下，必须设计自适应滤波器，以使得滤波器的动态特性随着信号和噪声的变化而变化，以达到最优的滤波效果。
还学习了小波变换本文介绍了使用小波完成：间断点识别、时频分析(短时傅里叶变换)、信号去噪。下面把文中得到的一些有用结论再列举如下：小波域的高频细节的系数图像，专门用来检查原始信号间断点；随着分解级数的增加，最高级高频细节的系数图像几乎只反映间断点位置！时频分析的目的是观察原始信号中频率随时间的变换规律，窗口大小是个较为关键的参数；现实情况时频图基本上都是连在一起的；小波去噪用到的函数较多，并且很多时配套使用。
我认为接下来的学习是可以跟我的专业是相关的，基本已经确定的方向是3D打印机的故障诊断，因为这里面不仅仅还要采用视觉信息故障诊断，而且还会加入到声音震动这些性进行负荷诊断，因此小波变化是非常有用的3D打印机的故障诊断暂时分为四大类，一个是断丝，然后第二个是有层纹，第三个就是有拉丝，第四个模型就脱离平台，至于大的方面，可以采用视觉进行卷积神经网络进行区分，针对有成文和拉丝这一块儿可以采用声音传感器，进行细微的划分。再次感谢老师和同学！！！

这篇关于【现代信号处理第六次作业】的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！


http://www.chinasem.cn/article/567842。

相关文章

Go信号处理如何优雅地关闭你的应用

Go信号处理如何优雅地关闭你的应用

《Go信号处理如何优雅地关闭你的应用》Go中的优雅关闭机制使得在应用程序接收到终止信号时,能够进行平滑的资源清理,通过使用context来管理goroutine的生命周期,结合signal... 目录1. 什么是信号处理？2. 如何优雅地关闭 Go 应用？3. 代码实现3.1 基本的信号捕获和优雅关闭3.2
阅读更多...
作业提交过程之HDFSMapReduce

作业提交过程之HDFSMapReduce

作业提交全过程详解 （1）作业提交 第1步：Client调用job.waitForCompletion方法，向整个集群提交MapReduce作业。 第2步：Client向RM申请一个作业id。 第3步：RM给Client返回该job资源的提交路径和作业id。 第4步：Client提交jar包、切片信息和配置文件到指定的资源提交路径。 第5步：Client提交完资源后，向RM申请运行MrAp
阅读更多...
深入理解RxJava：响应式编程的现代方式

深入理解RxJava：响应式编程的现代方式

在当今的软件开发世界中，异步编程和事件驱动的架构变得越来越重要。RxJava，作为响应式编程（Reactive Programming）的一个流行库，为Java和Android开发者提供了一种强大的方式来处理异步任务和事件流。本文将深入探讨RxJava的核心概念、优势以及如何在实际项目中应用它。 文章目录 💯 什么是RxJava？💯 响应式编程的优势💯 RxJava的核心概念
阅读更多...
Java高级Day38-网络编程作业

Java高级Day38-网络编程作业

112.网络编程作业 //1.使用字符流的方式，编写一个客户端程序和服务器端程序//2.客户端发送"name"，服务器端接收到后，返回"我是nova"//3.客户端发送"hobby"，服务器端接收到后，返回"编写java程序"//4.不是这两个问题，回复"你说啥呢"​​===============//客户端//===============public class SocketT
阅读更多...
0906作业+思维导图梳理

0906作业+思维导图梳理

一、作业： 1、创捷一个类似于qq登录的界面 1）源代码 #include "widget.h"#include "ui_widget.h"Widget::Widget(QWidget *parent): QWidget(parent), ui(new Ui::Widget){ui->setupUi(this);//QPushbutton:登录、退出this->join = new QP
阅读更多...
TCP/IP协议栈详解及其在现代网络中的应用

TCP/IP协议栈详解及其在现代网络中的应用

在当今数字化时代，网络已成为我们生活中不可或缺的一部分。无论是社交、工作还是娱乐，网络都在背后发挥着至关重要的作用。而这一切的实现，都离不开TCP/IP协议栈。本文将详细介绍TCP/IP协议栈的结构、各层功能以及它在现代网络中的应用。 什么是TCP/IP协议栈？ TCP/IP协议栈，全称为传输控制协议/互联网协议栈（Transmission Control Protocol/Internet
阅读更多...
构建现代API：FastAPI中Query与Body参数的最佳搭配

构建现代API：FastAPI中Query与Body参数的最佳搭配

在FastAPI中，Query 和 Body 是两种不同的依赖注入器，它们的应用场景取决于你的具体需求。以下是它们各自常见的使用场景： Query 参数 使用场景： 当你需要从URL中获取一些简单的参数时，例如过滤、排序、分页等。 当数据量不大，且可以作为URL的一部分安全传输时。当数据不需要复杂的结构时。 Body 参数 使用场景： 当你需要发送较为复杂的数据结构时，例如包含多个字段
阅读更多...
2024.9.6 作业

2024.9.6 作业

1> 手写unique_ptr指针指针 #include <iostream>using namespace std;template <typename T>class my_unique_ptr{public:explicit my_unique_ptr(T *p = nullptr) noexcept // 构造函数{ptr = p;}~my_unique_ptr() noexcep
阅读更多...
9月6号作业

9月6号作业

1：.h文件 #ifndef MAINWINDOW_H #define MAINWINDOW_H #include <QMainWindow> #include <QWidget> #include<QIcon> //图标类 #include<QLabel> //标签类 #include<QMovie> //动图类 #include<QLineEdit> //行编辑器类
阅读更多...
【数字信号处理】一文讲清FFT(快速傅里叶变换)

【数字信号处理】一文讲清FFT(快速傅里叶变换)

目录 快速傅里叶变换（Fast Fourier Transform，FFT）FFT的背景快速傅里叶变换（Fast Fourier Transform，FFT）DFT的数学表达实际计算重要性和应用频谱泄露、频谱混叠奈奎斯特采样定理参考链接 快速傅里叶变换（Fast Fourier Transform，FFT） FFT的背景 1、为什么要时域→频域频率？50Hz+频率120Hz
阅读更多...

Copyright China编程 23002807@qq.com

沪ICP备2023033072号-2