《Quantum state transfer on unsymmetrical graphs via discrete-time quantum walk》论文解读

本文仅仅代表个人的读后感，如有不对，欢迎大家指出呀~

论文简要概述

这篇论文是针对butterfly-network上的量子态转移的研究。
它的核心思想就是将butterfly network转化成二部图（因为处理二部图有一个比较完整的流程，并且保真度挺高）

1.introduction

第一部分主要是讲quantum walk、perfect state transfer等一些背景的介绍。

2.Preliminaries

第二部分主要是论文的预备知识。
（1）二分图的介绍
（2）butterfly-network的介绍
（3）将butterfly-network转化成二分图。
如下图中的（a）是butterfly-network，然后可以转换成（b）中的二分图的形式。

3.Quantum State Transfer Over the Butterfly Network via Discrete-Time Quantum Walk（核心部分）

这一部分就是和完全二部图的量子态转移的过程相同。

1. 定义初态、终态

量子态转移的目标就是从顶点1转到顶点6.

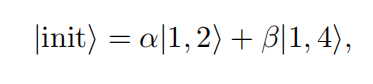
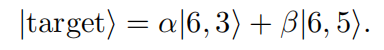
2. 定义coin-operator

在标记点使用的是I当做coin-operator,在非标记点使用的是G.

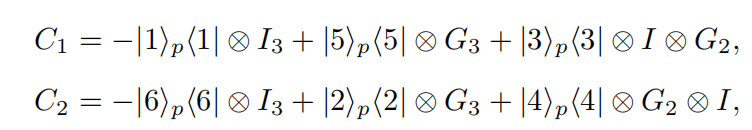
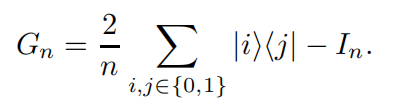
3. 定义shift-operator

shift-operator就是从在图里面进行移动，有那个边的就可以移动。

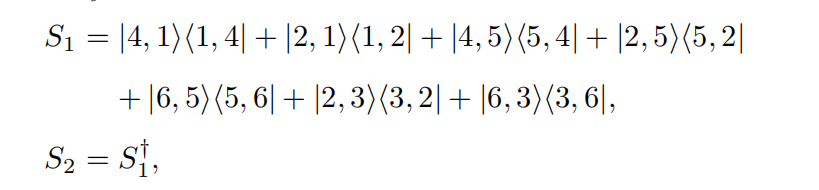
4.定义U

(1)U是先进行coin-operator的操作

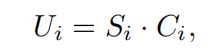
（2）由于初态和终态在不同侧，所以要对初态先进行一次U操作，让初态和转移到和终态同一侧。

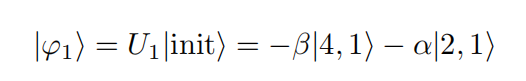
（3）现在初态和终态在同一侧了，所以如果最终转移到终态时，则必定经过了偶数次U操作，而且是先进行U2，再进行U1,所以定义了Ueff.

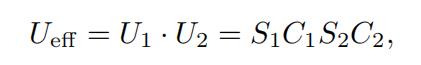
5. U在一组标准正交基下的矩阵表示，并求改矩阵的特征值和特征向量。

这组正交基就是把二部图下的所有边都表示出来，并且基与基之间的内积为0.这里的每一条边都是正交的，所以把这七条边当成一组标准正交基。

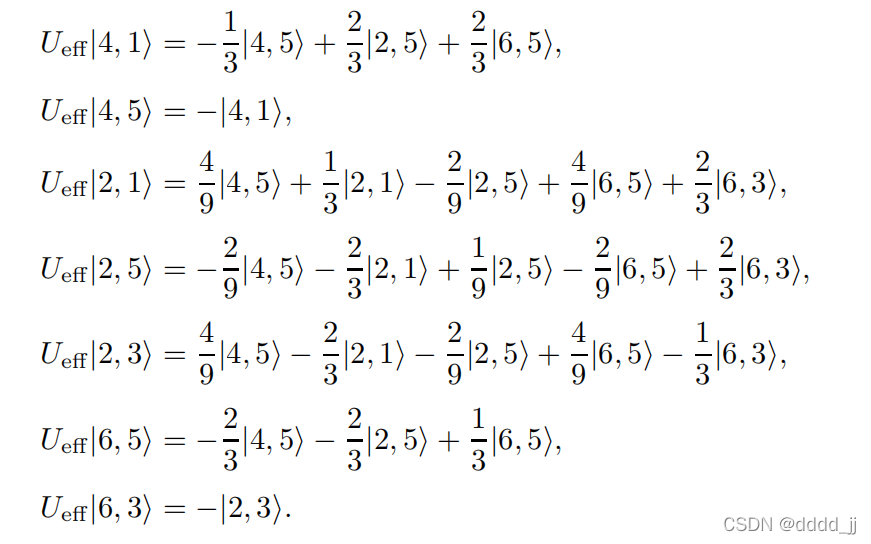
所以，在这组标准正交基的矩阵表示为如下：

求出改矩阵的特征值和特征向量。

6.将初态、终态用特征向量表示出来。

初态用特征向量进行表示。

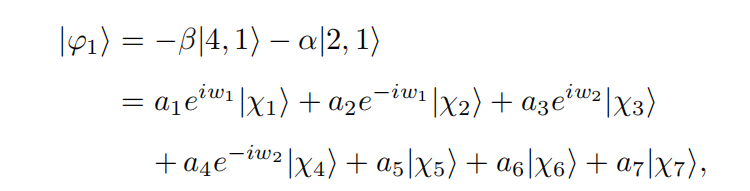
初态经过了t次之后，变成的状态。

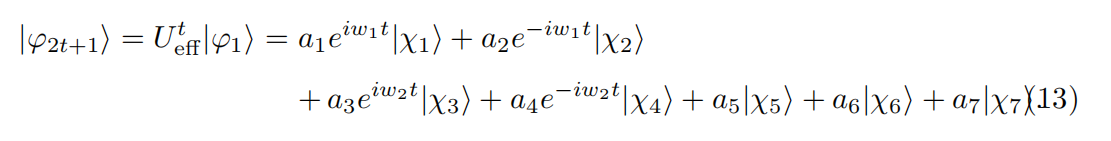
终态用特征向量表示出来。

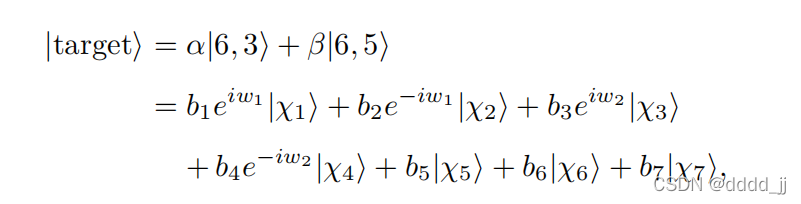
7.计算保真度

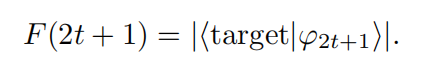
最终经过计算，发现保真度和要传输的量子态有关。

4.Conclusion

结论就是发现，保真度与要传输的量子态有关。

5.论文读后感

其实个人不太赞同它的结论，个人觉得保真度与图的每个顶点的度有关，但是可以借鉴它的方式，把一些不对称的图，转移到对称的图上。