HoudiniVex笔记_P13_TrigonometryBasics三角函数

本文主要是介绍HoudiniVex笔记_P13_TrigonometryBasics三角函数，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

原视频：https://www.youtube.com/playlist?list=PLzRzqTjuGIDhiXsP0hN3qBxAZ6lkVfGDI
Bili：Houdini最强VEX算法教程 - VEX for Algorithmic Design_哔哩哔哩_bilibili

Houdini版本：19.5

1、度和弧度

角度的两种表达方式：度【°】和弧度【π】。
在Houdini里的大多数情况下，需要将角度转换成弧度进行计算。
π=180°≈3.14=圆周长/直径。

eg.可使用类型为detail的attributeWrangle节点验证以下代码：

float degrees = chf('degrees');
float radians = chf('radians') * PI * 2.0;;f@radians = radians(degrees);   //若degrees=180，则radians≈3.14159
f@degrees = degrees(radians);   //若radians=1,则degrees=360
f@pi= PI;                       // pi ≈ 3.14

2、π计算

略

3、正弦sin、余弦cos、正切tan

如下图所示，在单位为1的圆内，正弦sinθ = b，余弦cosθ = c，正切tanθ = b/c，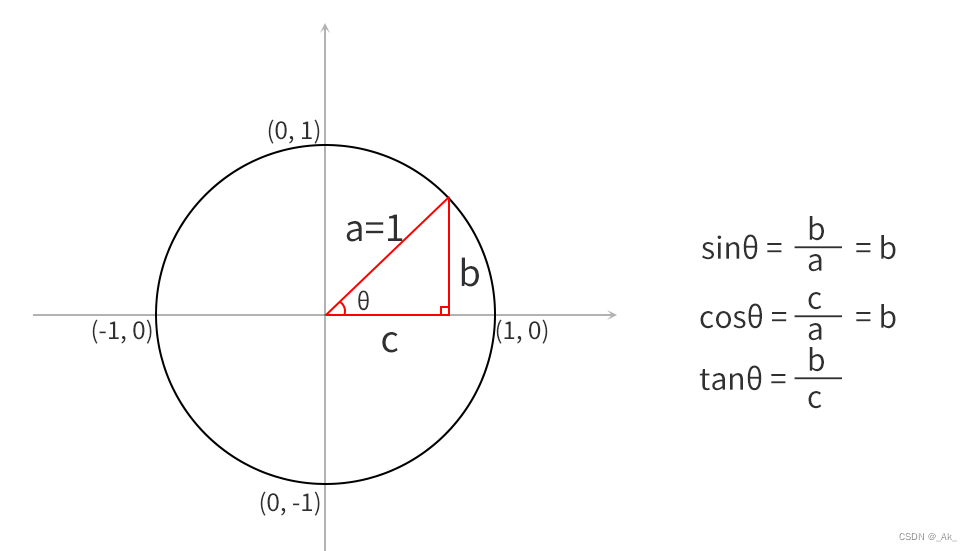

4、三角函数可视化

eg.①首先搞条z轴旋转45°的直线/Transform节点的旋转z轴(方便理解)

②以这条线为直角三角形的斜边，创建另外两条边，并设置detail属性，分别在PointWrangle中输入代码：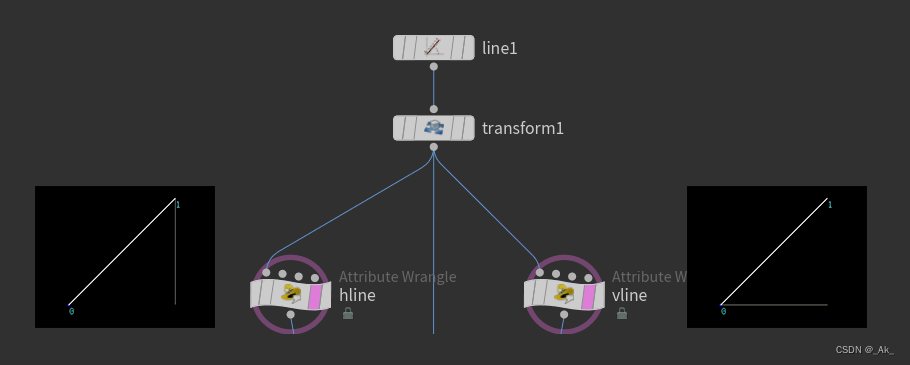

//PointWrangle节点hline    
if(@ptnum == 1){@P.y = 0.0;setdetailattrib(0, 'c', @P.x);
}

//PointWrangle节点vline
if(@ptnum == 0){vector npos = point(0, 'P', 1);@P.x = npos.x;
}if(@ptnum == 1){setdetailattrib(0, 'b', @P.y);
}

③合并三条边之前，先用测量节点measure确定斜边的长，以及用attribpromote节点把斜边长度转为detail属性：

④三边合并，并添加一个以斜边为半径的圆合并：
其中圆的半径引用斜边的长度【复制—粘贴参数引用】，

⑤最后在，mergre下添加一个类型为detail的AttributeWrangle节点，写入以下代码：

float rad = chf('rad');             //自定义半径
float ang = radians(chf('ang'));    //自定义角度float a = f@a;  //高度
float b = f@b;  //宽度
float c = f@c;  //斜边f@sinval = b/a;
f@cosval = c/a;
f@tanval = b/c;f@sinval2 = sin(ang);
f@cosval2 = cos(ang);
f@tanvla2 = tan(ang);f@b2 = sin(ang) * a;
f@c2 = cos(ang) * a;

其中，自定义半径<——斜线【复制—粘贴参数引用】、自定义角度<——Transform节点的旋转z轴【复制—粘贴参数引用】，

结果：略

5、练习1——画圈圈

eg.利用sin、cos函数画圈圈。在类型为detail的attributeWrangle节点写入以下代码：

int num = chi('num');
float rad = chf('rad');for(int i =0; i<num; i++){float ang = 2.0 * $PI / num * i;    //角度递增，最大为360°float x = cos(ang) * rad;float y = sin(ang) * rad;vector pos = set(x, y, 0);int pt = addpoint(0, pos);
}    //结果如下：

6、练习2——画转圈圈

先上结果：小球从最左点开始绕圈圈运动。

操作：
类型为Points的AttributeWrangle节点(命名为oribt)写入以下代码：

float ang = radians(chf('ang'));    //角度、范围设为0~360
float rad = chf('rad');             //半径、大小随意float x = cos(ang) * rad;       //x坐标
float y = sin(ang) * rad;       //y坐标@P = set(x, y, 0);

其它设置：add节点(添加1个点)、sphere节点(polygon、缩小)、circle3节点的缩放<——oribt节点的半径通道rad【复制—粘贴参数引用】、oribt节点的角度通道Ang写成【$FF / $FEND * 360】。

7、练习3——画大波浪

大概就是利用三角函数画出它们的坐标图。

eg.在类型为detail的attributeWrangle节点写入以下代码：

int num = chi('num');
int switch = chi('switch');   //根据输入的数字，切换不同三角函数计算方式for(int i=0; i<num; i++){float ang = $PI * 2.0 *i / num * chf('wavenum');    //起伏幅度次数，即角度大小float x = ang;float y = 0.0;if(switch == 0){y = sin(ang);}else if(switch == 1){y = cos(ang);}else if(switch == 2){y = tan(ang);}vector pos = set(x, y, 0.0);int pt = addpoint(0, pos);
}

结果大概是类似下面这种样子：

8、练习4——沿着大波浪动

eg.如下图添加节点，其中add节点(添加一个点)、animate_wave节点(points类型)，

在animate_wave中输入以下代码：

float ang = radians(chf('ang'));    //设置范围0~360float x = ang;        //若x=0，小球将上下运动
float y = sin(ang);@P = set(x, y, 0);

其中，在通道角度ang中输入【$FF / $FEND * 360 * 2.0】(2.0为自定义倍速)
结果为：小球运动规律符合sin函数规律。

9、三角函数值范围

如下图所示，图片来自@门酱胡安，图一为sin、cos函数图像，第二章为tan函数图像。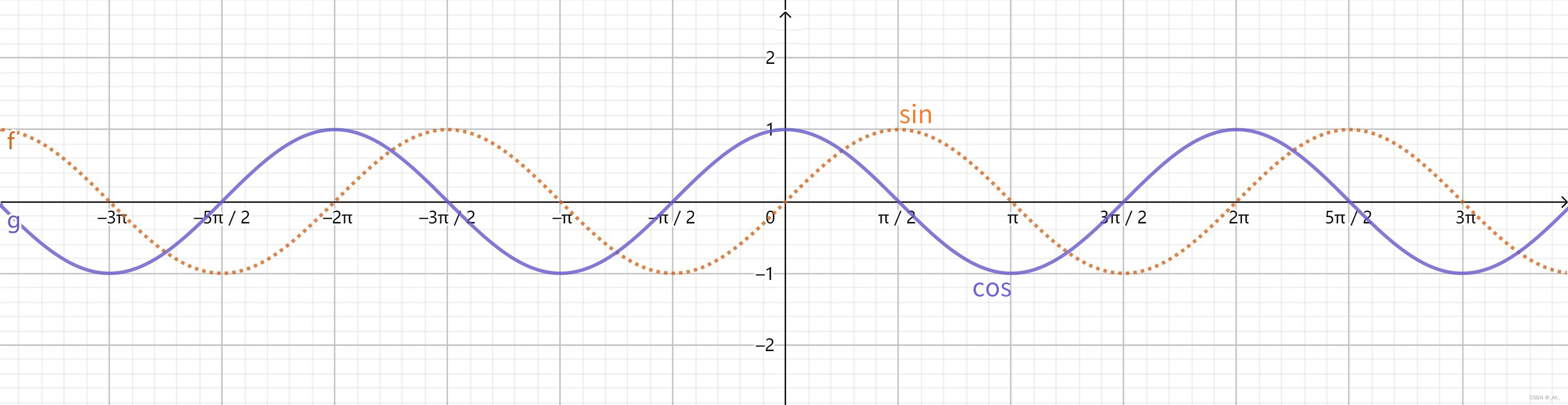

如若不懂，可以结合【3、正弦sin、余弦cos、正切tan】的图像去理解。

10、练习5——动态缩放

eg.Sphere小球节点(polygon)、PointWrangle节点，并写入以下代码：

float val = cos($PI * 2.0 * @Frame / $FEND * 2);    // *2仅是让小球缩放快些val = fit(val, -1.0, 1.0, 0.1, 1.0);    //映射函数，把val值(-1.0, 1.0)，映射到(0.1， 1.0）@P *= val;

结果：小球缩放规律类似cos函数

11、反三角函数

这里大概看看就好，深入了解可以看这篇文章的推导过程。

常用的另外三个三角函数：
cot余切=1/正切=邻边/对边，
sec正割=1/余弦=斜边/邻边，
csc余割=1/正弦=斜边/对边。

反三角函数：反正弦arcsin、反余弦arccos、反正切arctanx。可以理解为将原三角函数的x、y调换位置所得，如图所示，

反函数的导数等于直接函数的导数的倒数: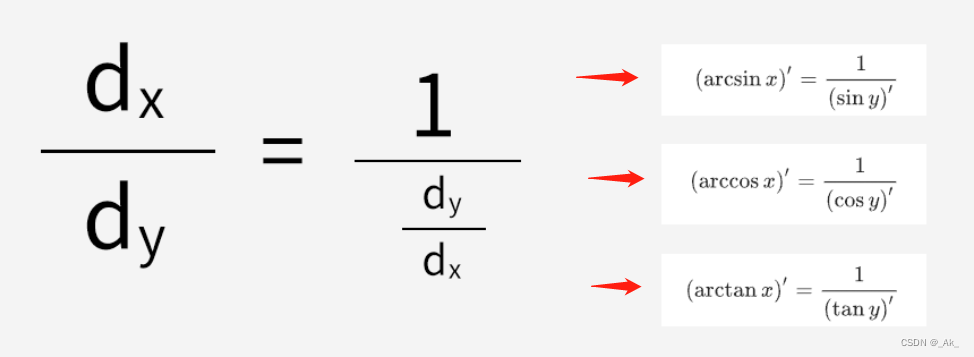

eg、可以在类型为detail的attributeWrangle节点写入以下代码，并结合前面代码验证另外三个三角函数结果：

//余割、余切、正割
float ang = radians(chf('ang'));f@cosecant = 1.0 / sin(ang);
f@secant = 1.0 / cos(ang);
f@cotangent = 1.0 / tan(ang);

12、使用反三角函数获取角度

使用反三角函数估算角度，多少有点不完美，使用 atan2() 函数完美解决。

eg.直接使用【4、三角函数可视化】的案例，仅对最后的attributeWrangle节点的代码进行修改，

float rad = chf('rad');             //自定义半径
float ang = radians(chf('ang'));    //自定义角度float a = f@a;  //高度
float b = f@b;  //宽度
float c = f@c;  //斜边f@sinval = b/a;
f@cosval = c/a;
f@tanval = b/c;f@sineang = degrees(asin(f@sinval));    //当角度位于180°~270°~360°时，得到的角度值从0°开始到-90°再到0°
f@cosang = degrees(acos(f@cosval));     //当角度位于180°~270°~360°时，得到的角度值为180°~0°
f@tanang = degrees(atan(f@tanval));     //当角度位于90°~270°、270°~360°时，得到的角度值为-90°~90°，-90°~0°//用Houdini自带的atan2()函数完美解决角度估算问题
// atan2() 函数仅需要x、y值(两条直角边)
f@tanang2 = degrees(atan2(b, c));

结果：略

13、练习6——两向量角度

理论：如下图所示，求向量A、B的夹角角度。
①对向量A进行归一化，利用点积求得边长a的值；
②勾股定理，a²+b²=c²，求得b值（c²=x²+y²+z²）；
③反函数atan2()求得角度θ。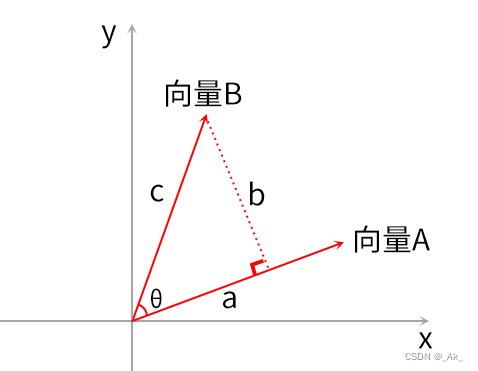

eg.按下图设置创建两条直线，通道参数可直接拖拽创建：通道与直线的旋转【复制—粘贴参数引用】，当然也可以对直线直接设定恒定旋转值，以验证结果。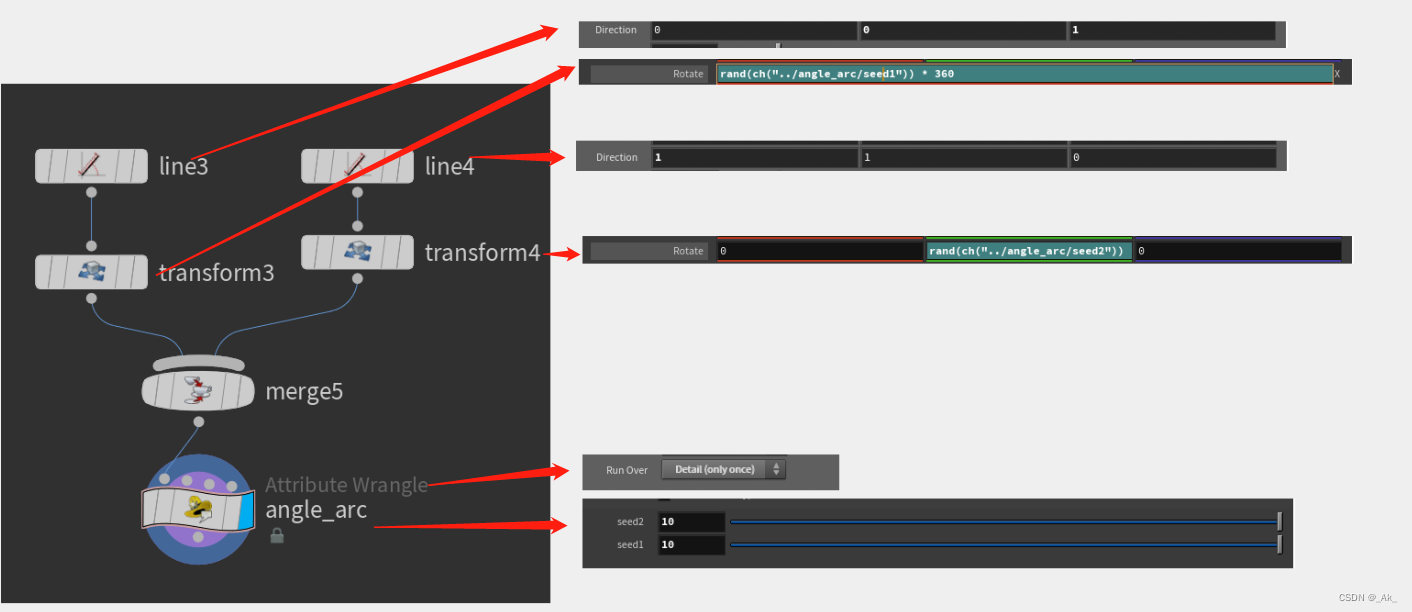

在angle_arc输入以下代码：

//根据直线首末两个顶点坐标，获取向量值
int pts1[] = primpoints(0, 0);
int pt11 = pts1[0];
int pt12 = pts1[1];
vector pos11 = point(0, 'P', pt11);
vector pos12 = point(0, 'P', pt12);
vector dir1 = pos12 - pos11;           //根据直线首末两个顶点坐标，获取向量值
int pts2[] = primpoints(0, 1);
int pt21 = pts2[0];
int pt22 = pts2[1];
vector pos21 = point(0, 'P', pt21);
vector pos22 = point(0, 'P', pt22);
vector dir2 = pos22 - pos21;float dot = dot(normalize(dir1), dir2);     //根据点积，求得a值
float vlen = length(dir2);                  //向量B的长度
float h = sqrt(pow(vlen, 2) - pow(dot, 2)); //勾股定理，求得b值float ang = atan2(h, dot);                  //反三角函数，求得角度f@ang = degrees(ang);                       //两个向量之间的夹角

结果：略

14、练习——两向量之间画弧

理论：①根据叉乘，可以得到两个向量的垂直向量，即法线向量，暂且将其定为(虚假的)Z轴；
②把其中一个向量作为(虚假)的X轴，与Z轴求得(虚假的)Y轴；
③(虚假)X、(虚假)Y轴所构成的平面就是两个向量之间构成的平面；用三角函数sin、cos即可求得生成点在(虚假)X轴、(虚假)Y轴上的坐标。

直接使用【13、Exercise练习6——两向量角度】的项目，对代码进行修改为，

//根据直线首末两个顶点坐标，获取向量值
int pts1[] = primpoints(0, 0);
int pt11 = pts1[0];
int pt12 = pts1[1];
vector pos11 = point(0, 'P', pt11);
vector pos12 = point(0, 'P', pt12);
vector dir1 = pos12 - pos11;           //根据直线首末两个顶点坐标，获取向量值
int pts2[] = primpoints(0, 1);
int pt21 = pts2[0];
int pt22 = pts2[1];
vector pos21 = point(0, 'P', pt21);
vector pos22 = point(0, 'P', pt22);
vector dir2 = pos22 - pos21;float dot = dot(normalize(dir1), dir2);     //根据点积，求得a值
float vlen = length(dir2);                  //向量B的长度
float h = sqrt(pow(vlen, 2) - pow(dot, 2)); //勾股定理，求得b值float ang = atan2(h, dot);                  //反三角函数，求得角度f@ang = degrees(ang);                       //两个向量之间的夹角//上面代码与前面相同//画弧
vector xaxis = normalize(dir1);             //其中之一的向量归一化，虚假的X轴
vector zaxis = normalize(cross(xaxis, normalize(dir2)));    //两个向量的垂直向量，即法线向量，虚假的Z轴
vector yaxis = normalize(cross(zaxis, xaxis));              //虚假的Y轴int num = chi('num');
for(int i=0; i<num; i++){float sang = ang * i / (num - 1.0);             //对两个向量之间的夹角进行细分float x = cos(sang);                    //生成点的宽度，即直角三角形的宽度边float y = sin(sang);                    //生成点的高度，即直角三角形的高度边vector tx = xaxis * x;                  //生成点在(虚假X轴)方向的宽度/坐标vector ty = yaxis * y;                  //生成点在(虚假Y轴)方向的高度/坐标//为什么没Z轴？因为我们是以(假)X轴和(假)Y轴为平面，生成弧度点vector tpos = tx + ty;                  // "X"、"Y"轴的坐标相加，得到具体位置int pt = addpoint(0, tpos);
}

结果大概是这个样子：