电子学：第011课——实验 9：时间与电容器

电子学：第011课——实验 9：时间与电容器

实验 9：时间与电容器

电子能够以接近光速的速度运动，但我们仍然可以使用它们以秒、分钟甚至小时为单位测量时间。这个实验将向你展示如何测量时间。

需要的物品

• 面包板、连接线、剪线钳、剥线钳、测试引线、万用表
• 9 V 电池和连接器 1 个
• 触摸开关 2 个
• 通用 LED 1 个
• 电阻器：470 Ω、1 kΩ、10 kΩ 各 1 个
• 电容器：0.1μF、1 μF、10 μF、100μF、1000 μF 各 1 个

给电容器充电

首先，设置万用表为测量直流电压，用万用表测量 9 V 电池的电压。如果电池电压小于 9.2 V，那么你需要用一块新电池进行本实验。

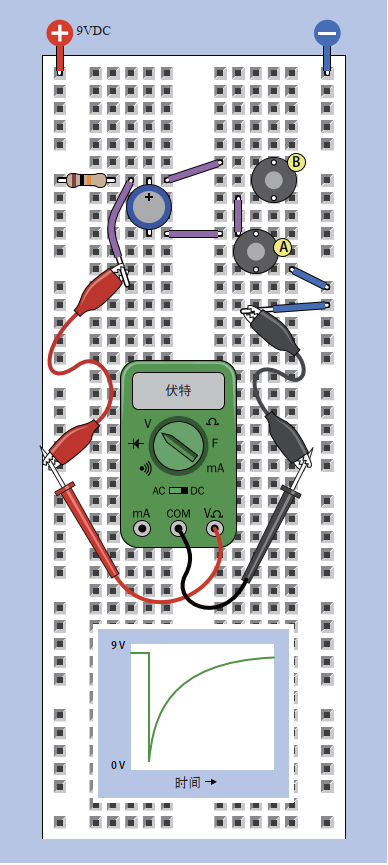
在面包板上安装两个触摸开关、一个 1 kΩ 电阻器和一个 1000 μF 电容器，如图 2-79 所示。使用几根测试引线连接万用表，这样就可以测量电容器两引脚之间的电压，同时不占用双手。

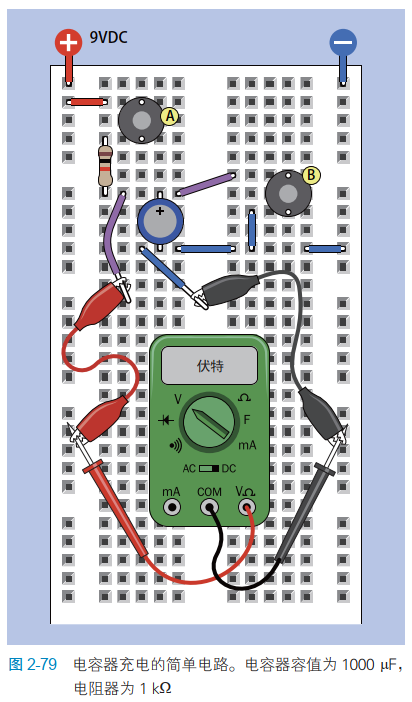
把连接器紧扣在电池上，导线插入面包板，向面包板的两根总线提供 9 V 直流电，左侧总线连接电源正极，如图所示。

如果万用表测得的电压大于 0.1 V，就按压B按钮，让电容器的两侧短接，从而使其放电。

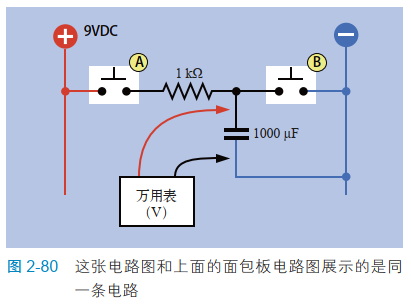
图 2-80 中的电路图展示了相同的电路，能够帮助你了解原理。

现在按住按钮 A，用手表、钟表或手机计时，看电容器充电到 9 V 需要多少秒。如果你使用的是自调量程万用表，随着电荷的增加，它应当自动从一开始的测量毫伏变化为测量伏特。我做这个实验时，万用表完成变化只用了 3 秒。

随着越来越多的电子空穴和电子被吸引到电容器的两个极板上，电容器的正极板变得更“正”，负极板变得更“负”了。电流不能通过电容器，因此电容器两引脚间的电势差增加。在任何一本入门电子学教材中，你最先看到的一条结论就是：

电容器阻碍直流

只要你给电容器两端施加稳定的电势差，就能得到这个结论。

RC 网络

拆下 1 kΩ 的电阻器，换上 10 kΩ 的电阻器。如果万用表显示电容器两端仍有电压，就按住按钮B 给电容器放电。

现在重复测试。电容器通过 10 kΩ 的电阻器充电到 9 V 需要多长时间？

电容器和电阻器的简单组合称为 RC 网络（R 代表电阻器，C 代表电容器）。这是一个非常重要的电子学概念。在我解释 RC 网络的原理之前，先考虑以下几个问题。

• 把 1 kΩ 电阻器换成 10 kΩ 电阻器后，电容器充电到 9 V 用的时间恰好是原来的 10 倍吗？
• 电容器两端的电压是匀速增加，还是先快后慢或者先慢后快？
• 如果等上足够长的时间，电容器两端的电压会达到电池电压的初始测量值吗？

电压、电阻和电容

把电阻器想象为一个限制水流的水龙头，把电容器想象成一个等待灌满的气球（见图 2-81）。
如果你拧紧水龙头，只让水一滴滴地流出，气球灌满的时间就要长一些，但是只要你等的时间足够长，很小的水流也能灌满气球。假设气球不会
爆炸，那么当气球内部的压力等于供水管中的水压时，这个过程就会结束。

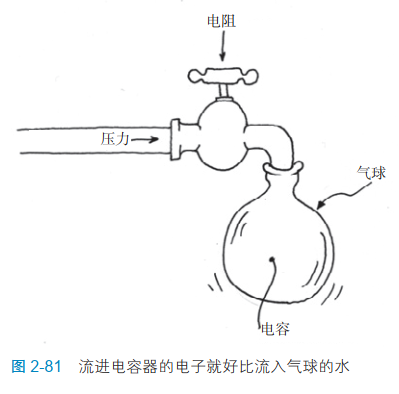
但是这种描述遗漏了一个重要的因素。随着气球充满水，它会伸长，对内部的水施加更多的压力。随着气球内部压力增大，水的流入会受阻。因此，在这个过程中，我们可以预计水流的速度减慢。

这个过程是如何与电子流入电容器的过程相类比的呢？概念很简单。起初，电子源源不断地涌入电容器，但是随着它们占据越来越多的电子空穴，新进入的电子就需要更长时间才能找到位置。充电的速度因此变得越来越慢。实际上，理论上讲，电容器两端的电压永远无法达到充电电压。

背景知识：时间常量

电容器的充电速度以“时间常量”函数计量。时间常量的定义很简单：
$$T=R\times C$$
T 单位为秒，是电容器的容值为 C（单位为法拉）通过阻值为 R 的电阻器充电所用的时间常数。

回到第一次测试的电路，使用 1 kΩ 的电阻器，我们可以把各个元件的值代入时间常数公式中——但是要把单位转换成欧姆和法拉。1 kΩ 是 1000 Ω，1000 μF 是 0.001 F。这样计算就很容易了。
$$TC=1000\times 0.001$$

因此，对于所取的阻值和容值，TC=1。
但是 TC 究竟有什么意义呢？它是不是指电容器在一秒钟内就能充满电呢？很遗憾，并不是那么简单。

• 时间常量 T 是电容器从 0V 开始至获得所供给的电压的 63% 所需的时间（秒）。

如果电容器的初始电压不是 0V，又会怎么样呢？如果我们测量的时候电容器已经获得了初始电压，定义就有些复杂了。设 $V_{DIF}$ 是电容器两端电压和电源电压的差值，T 就是电容器在已有电荷基础上，增加 $V_{DIF}$ 的 63% 电压所用的时间。

（为什么是 63%，而不是 62%、64% 或 50% 呢？这个问题的答案对于本书来说过于复杂了，如果你想了解更多关于时间常数的知识，就需要去查阅其他资料。准备好学习微分方程。）

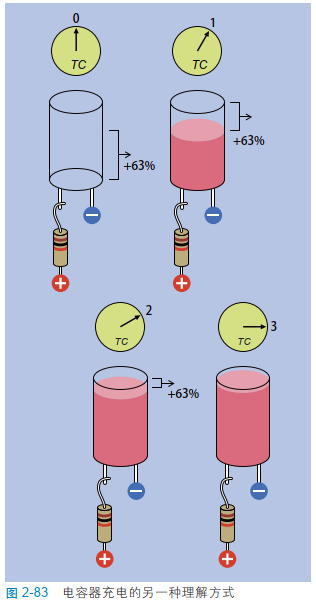
也许打个比方会有助理解。图 2-82 画了一个贪吃的人，他正准备吃一块蛋糕。一开始，他实在饿极了，于是他切下 63% 的蛋糕，1 秒钟吃完了它，1 秒钟就是他吃蛋糕的时间常量。第二次吃的时候，他切下了剩余蛋糕的 63%——他不再觉得那么饿了，他吃下这块蛋糕又用了 1 秒钟（记住，这是他的时间常量）。第三次，他再切下剩余蛋糕的 63%，仍然用 1 秒钟吃完，以此类推。他逐渐吃下整块蛋糕，就如同电容器逐渐充满电子。但是他永远吃不完整块蛋糕，因为他只取剩余蛋糕的 63%。

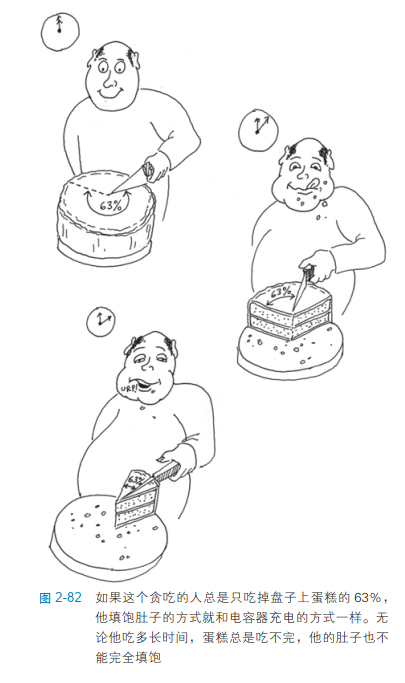
图 2-83 以另一种方式展示了这个过程。在每个时间常量（若使用的是 1000 μF 电容器和 1 kΩ 电阻器，常量就为 1 s）之后，电容器的电压都会增加它原有电压和电源电压差值的 63%。

在一个使用理想元件的理想世界里，电容器的充电过程将永远持续。在现实世界里，我们专横地规定：

五个时间常量之后，电容器上的电荷接近100%充满，可以认为充电完成。

背景知识：绘制曲线图

我想画出一条曲线图，展示电容器两端电压随电容器充电的变化情况。为此，我将使用时间常量公式计算数据。

设 $V_{CAP}$是电容器两端当前的电压，而 $V_{DIF}$ 是该电压与电源电压的差值（同前）。下面的公式将告
诉我一个时间常量之后，电容器两端的电压是多大。设这个新电压值为 $V_{NEW}$。公式如下：
$V_{NEW}=V_{CAP}+(0.63\times V_{DIF})$

设电池电压为 9 V，电容器起始电压为 0 V。则 $V_{CAP}$ = 0，$V_{DIF}$ = 9。将以上数值代入公式：
$V_{NEW}=0+(0.63\times 9)$
计算器得到 0.63×9 = 5.67。因此，在一个时间常量（1 s，R = 1 kΩ，C = 1000 μF）之后，电容器两端的电压达到 5.67 V。
下一秒情况如何？我们需要使用新的值重复计算。电容器两端的电压 $V_{CAP}$ 现在为 5.67 V，电池电压仍为 9 V，因此 $V_{DIF}$ 等于 9 减去 5.67，即 3.33。将这些值代入同一个公式：
$V_{NEW}=5.67+(0.63\times 3.33)$
计算器得到 0.63×3.33 ≈ 2.1，而 2.1 + 5.67 = 7.77。因此，两秒钟后，电容器获得了 7.77 V 电压。
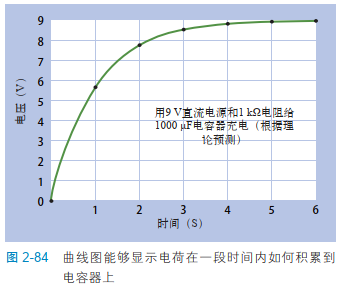
我们可以计算多次，得到一系列结果（保留两位小数），它们是电源电压为 9 V 时，每秒末电容器两端的电压：
1 秒后：5.67 V
2 秒后：7.77 V
3 秒后：8.54 V
4 秒后：8.83 V
5 秒后：8.94 V
6 秒后：8.98 V
图 2-84 中的曲线是根据上述数值绘出的平滑曲线。6 秒钟以后的值我没有计算，因为它们已经十分接近 9 V。

实验验证

我已经讲过如何计算 RC 网络中的电容器电量。但是你怎么知道我讲的对不对呢？应不应该直接相信我呢？

也许你应该自己测试一下。也就是说，你可以进行实验验证，这是发现学习法的重要组成部分。

回到你原先使用的电路，并确定电路里连接的是 10 kΩ 而非 1 kΩ 的电阻器。找个朋友坐在你旁边计时，你自己观察万用表上的电压示数。每隔 10 秒钟，朋友就说一声“好”，你则记录下此刻万用表显示的电压。整个过程持续大约一分钟。

因为你使用的是 10 kΩ 而非 1 kΩ 的电阻器，所以时间常量是 10 秒钟，而不是 1 秒钟。因此，你的读数应该和上文中我每隔一秒的一系列读数相似，只是时间间隔为 10 秒。

你测得的电压值应当与我测得的电压值相近，但不会完全一致。为什么呢？我能想到很多原因。

• 你的电池提供的电压与我的电池不完全一致。
• 你的电阻器的阻值不是恰好为 10 000 Ω。
• 你的电容器的容值不是恰好为 1000 μF。
• 你的万用表并不完全精确。
• 你在万用表上读数要用几微秒。
• 你的朋友不一定能完全精确地隔 10 秒钟提示一次。

还有两个因素你可能想不到。首先，电容器不能完美地储存电能。它们会漏电，逐渐漏掉其中的电荷。甚至在电容器充电时，漏电也在发生。在充电过程快结束时，电子流入的速度十分缓慢，与之相比，漏电现象（电子流出的速率）就十分显著了。

另外，你的万用表还有一定的内阻。它的阻值很高，但也客观存在。这就意味着在你测量电压时，万用表会从电容器上拿走一点电荷。于是测量过程就改变了你要测量的值！这确实是物理学和工程学面临的一个共同难题。

我可以想出很多方法来减小这些因素的影响，却无法彻底消除它们。实验误差总是存在，这是用实验验证理论时需要面临的挑战。理论的验证可能是一个很长的过程，需要很大的耐心——这就是理论家与实践者性格常常不同的原因。

电容耦合

既然已经讲过了电容器的充放电原理，我们就要回到前文得出的结论：

电容器阻碍直流

你可能还记得，我说过：“只要你给电容器两端施加稳定的电势差，就能得到这个结论。”

但是如果没有稳定的电势差，会怎么样？空电容器接上电源上的一瞬间会发生什么？

啊，这就另当别论了。在这些情况下，电容器会允许信号通过。

这怎么可能呢？电容器的两个极板互相不接触，电流怎么能从一片极板跳到另一片极板上呢？

我将在稍后解答这两个问题。首先，你需要确信我所说的现象确实会发生。
看一看图 2-85 中面包板上的元件，它们的布局与图 2-79 中的电路很像，但是 10 kΩ 的电阻器从左侧移到了右侧，还增加了一个 LED 和一个 470 Ω 的电阻器。

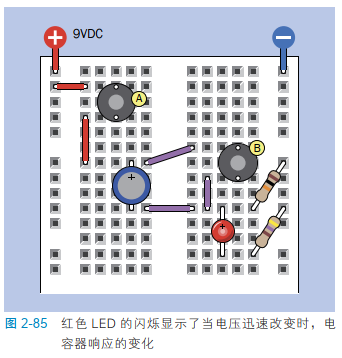
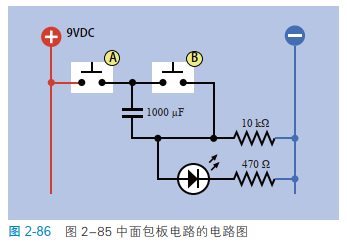
图 2-86 是面包板电路的电路图，可以帮助解释说明。

为避免混淆，我在图 2-87 中列出了各元件的值。

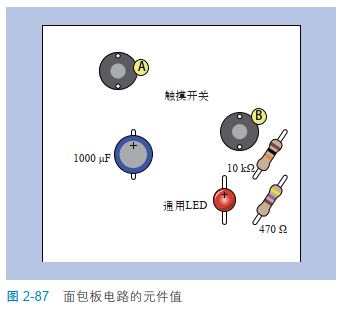
搭建好电路后，首先要记得按下按钮 B 给电容器放电。接着按下按钮 A——为什么 LED 开始闪烁，之后逐渐变暗了？

再次按下按钮 A。这一次几乎什么都没有发生，很明显，电容器刚才已经放电完毕，现在开始充电了。那么，再次按下按钮 B 来给电容器放电。现在再按下按钮 A，LED 又开始闪烁。

我们知道，电容器的下引脚上一开始几乎没有正电压，因为它通过 10 kΩ 电阻器连接到了负极。我们还知道，电容器的上引脚一开始也几乎没有正电压，因为按钮 B 把电容器的两个极板短接了。（这就是我让你给电容器放电的原因。）

然后你按下了按钮 A，它突然施加了一个正脉冲，电容器另一侧的 LED 点亮。通过 LED 的电流一定是从某个地方来的，而唯一的解释就是它来自电容器。

位移电流

让我们再试一试，把 LED 和串联电阻器换成万用表。图 2-89 展示了面包板布局，图 2-88 展示了电路图。按下按钮 B 给电容器放电，然后检查一下万用表的读数，应该为接近 0 V。

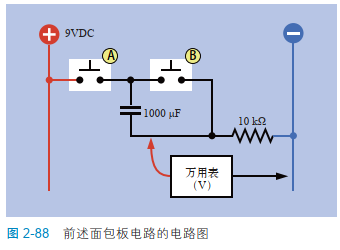
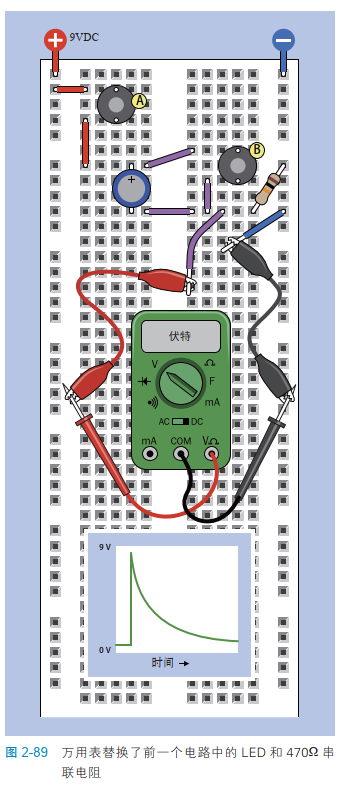
在按下按钮 A 的同时，仔细观察万用表。数字万用表的响应速度不太快，但在电压逐渐下降之后，你仍能发现电压骤然上升。

当我把示波器（可以测量和显示非常迅速的电压变化）连接到电路上时，显示出的波形看起来很像我在图 2-89 底部添加的曲线。电压上升得如此迅速，仿佛就在一瞬间。

瞬间变化的电压能够通过电容器，这一点我们已经熟知，电子学也经常用到这个原理。但这是为什么呢？

这个现象引起了一位早期的实验者詹姆斯 •麦克斯韦（James Maxwell）的兴趣，他觉得这一切无法用当时公认的理论来解释，于是他建立了一门理论，并创造了一个短语来描述他看到的现象。他称之为位移电流。这个名称与他当时正在研究的一些理论很契合。

今天，又有其他理论出现。很明显，电流的涌入在电容器内部引发了场效应，场效应可以在一对极板上产生电压。但是这个理论很快就变得十分复杂，大多数教材的讲解都很简略——电容器会阻碍直流，而允许波动的电压通过。”
如果换上一个更小的电容器，你就会发现，它允许更短暂的脉冲通过。取下万用表，把 LED 和470 Ω 串联电阻连回电路，分别连入 100 μF、10 μF、1 μF 和 0.1 μF 的电容器。连入最小的电容器时，LED 几乎不闪烁。

交流电

如果你把电路反向连接，虽然电流从相反的方向流入，但电路仍能工作。图 2-91 展示了反向连接后的电路，10 kΩ 电阻器移到了左侧，按钮 A移到了右侧。万用表仍然测量电阻器和电容器之间一点的电压。图 2-90 展示了同一个电路。

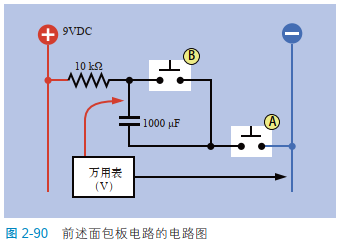
2-91 修改了前一个电路，电压反相

按下按钮 B 再松开，给电容器放电，此时万用表的读数约为 9 V 直流，电容器的上引脚通过 10 kΩ电阻器连接到了正极总线。电容器隔断直流，因此阻值约等于无限大，正电荷便“无处可去”。图 2-92展示了两个电阻器之间一点的电压如何随着该点与地之间阻值的增大而上升，从而解释了这个现象。

但是，当你按下面包板电路中的按钮 A 时，就产生了一个负脉冲。随着负脉冲通过电容器，电容器的等效电阻暂时消失，使得万用表的读数下降。然后，电容器缓慢充电，过程与本实验的第一次测试相同。

图 2-91 中的曲线图大致显示了电容器上电荷的变化情况。

• 电容器能阻碍直流。
• 电容器允许通过短暂的波动电流，无论电流方向如何。
• 之后，电容器积累电荷，过程如我在实验开始时所述。

这就引出了一个重要的结论。因为交流电（AC）是在正负之间迅速变换的一连串脉冲，所以电容器会允许它通过。
电容器的尺寸非常重要。用小容值的电容器进行同一个实验，你会发现它只会作出短暂的响应。小电容器能够通过高频的波动电流，同时又阻碍低频的波动电流——这一特性得到了很多应用，包括用于音频。在实验 29 中，你将自己尝试这一应用。记住，音频信号也是一种交流电，因为它们的变化速度很快。

当电容器连入电路用来通交阻直时，我们就称它为耦合电容。它可以允许信号从电路的一部分传递到另一部分，同时阻碍信号的直流电压，信号的两部分电压可能截然不同。在实验 11 中，我将使用这个概念。.