「NOIP2014」无线网络发射器选址

「NOIP2014」无线网络发射器选址 - 前缀和

本文主要是介绍「NOIP2014」无线网络发射器选址 - 前缀和，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

题目描述

随着智能手机的日益普及，人们对无线网的需求日益增大。某城市决定对城市内的公共场所覆盖无线网。

假设该城市的布局为由严格平行的129条东西向街道和129条南北向街道所形成的网格状，并且相邻的平行街道之间的距离都是恒定值1。东西向街道从北到南依次编号为0,1,2…128 , 南北向街道从西到东依次编号为0,1,2…128。

东西向街道和南北向街道相交形成路口，规定编号为x的南北向街道和编号为y的东西向街道形成的路口的坐标是（x,y）。在某些路口存在一定数量的公共场所。

由于政府财政问题，只能安装一个大型无线网络发射器。该无线网络发射器的传播范围
一个以该点为中心，边长为2*d的正方形。传播范围包括正方形边界。

例如下图是一个d=1的无线网络发射器的覆盖范围示意图。

noip2014

现在政府有关部门准备安装一个传播参数为d的无线网络发射器，希望你帮助他们在城市内找出合适的安装地点，使得覆盖的公共场所最多。

输入格式

第一行包含一个整数d，表示无线网络发射器的传播距离。

第二行包含一个整数n，表示有公共场所的路口数目。

接下来n行，每行给出三个整数x,y,k,中间用一个空格隔开，分别代表路口的坐标(x,y)以及该路口公共场所的数量。同一坐标只会给出一次。

输出格式

输出一行，包含两个整数，用一个空格隔开，分别表示能覆盖最多公共场所的安装地点方案数，以及能覆盖的最多公共场所的数量。

样例输入

1
2
4 4 10
6 6 20

样例输出

1 30

数据规模与范围

对于100%的数据, $1\le d\le 20,1\le n\le 20,0\le x,y\le 128,0\le k\le 1000000$

分析

由于本题数据范围较小，可以用暴力过，但我还是讲讲二维前缀和的做法。

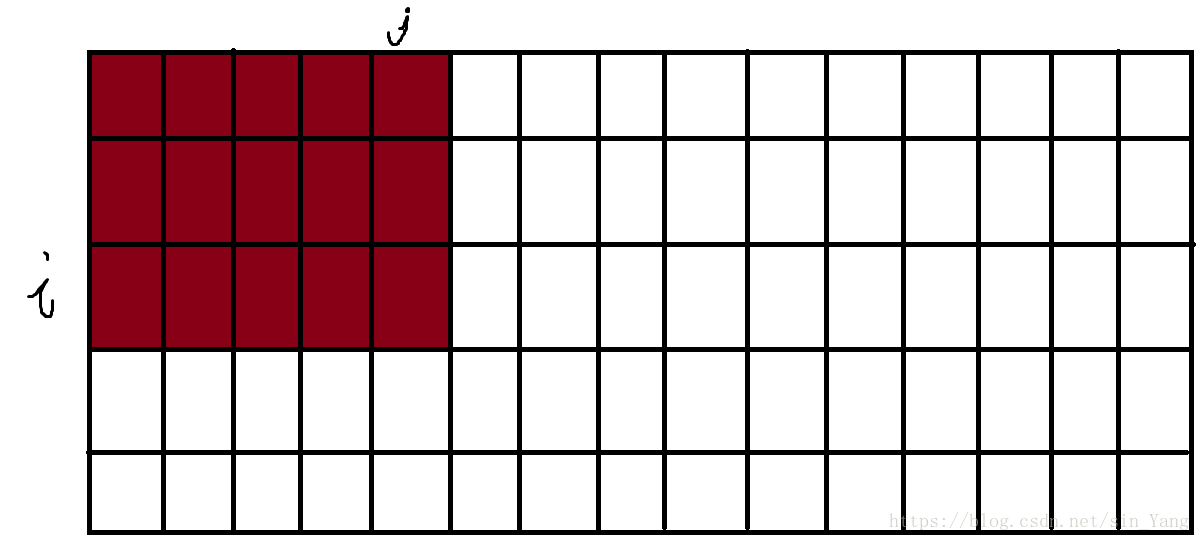
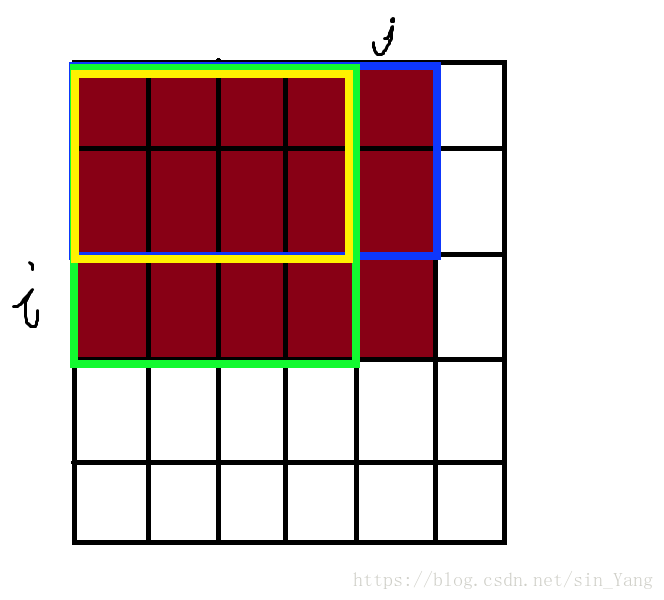
定义， $sum[i][j]$ 为前 $i$ 行前 $j$ 列在 $a[][]$ 中的和。所以， $sum[i][j]$ 就是下图中棕色区域的和。

这里写图片描述

通过这张图，也可以知道，棕色区域就等于蓝色框起来的区域和+绿色框起来的区域和-它们重叠的黄色区域和+右下角没有没覆盖到的棕色值。

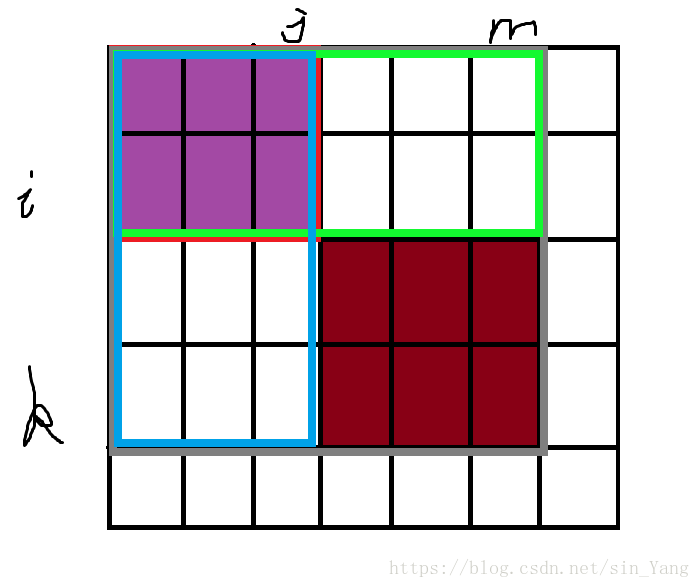
这里写图片描述

即

s u m [i] [j] = s u m [i - 1] [j] + s u m [i] [j - 1] - s u m [i - 1] [j - 1] + a [i] [j]

$sum[i][j]=sum[i-1][j]+sum[i][j-1]-sum[i-1][j-1]+a[i][j]$

这样我们就可以把前缀和算出来了。可要怎么快速查询 $a[i][j]-a[k][m]$ 的和？也很简单，如下图：

这里写图片描述

我们可以看到， $a[i][j]-a[k][m]$ 的和可以表示为棕色区域的和，而棕色区域的和就等于 $sum[j][m]-sum[i][m]-sum[k][j]$ 再加上多减的 $sum[i][j]$ ，即为

s u m [k] [m] - s u m [i] [m] - s u m [j] [m] + s u m [i] [j]

$sum[k][m]-sum[i][m]-sum[j][m]+sum[i][j]$

这样就可以在 $O(1)$ 时间内求解。

对于这道题，也是差不多的。

代码

#include <iostream>
#include <cstdio>
using namespace std;
int d,n;
long long sum[131][131],ans,cnt;
int g[130][130];
int main() {scanf("%d%d",&d,&n);for (int i = 1;i <= n;i++) {int a,b,c;scanf("%d%d%d",&a,&b,&c);g[a+1][b+1]=c;}for (int i = 1;i <= 129;i++)for (int j = 1;j <= 129;j++)sum[i][j]=sum[i-1][j]+sum[i][j-1]-sum[i-1][j-1]+g[i][j];//制造前缀和for (int i = 1;i <= 129;i++) {for (int j = 1;j <= 129;j++) {long long t=sum[min(i+d,129)][min(j+d,129)]-sum[max(i-d,1)-1][min(j+d,129)]-sum[min(i+d,129)][max(j-d,1)-1]+sum[max(i-d,1)-1][max(j-d,1)-1];//注意是从i+d,j+d到i-d,j-d的和if (t>ans) {ans=t;cnt=1;}else if (t==ans) {cnt++;}}}printf("%lld %lld",cnt,ans);return 0;
}