本文主要是介绍【教学类-43-11】 20231231 3*3宫格数独提取单元格坐标数字的通用模板（做成2*2=4套、3*2=6套），希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！
背景需求：
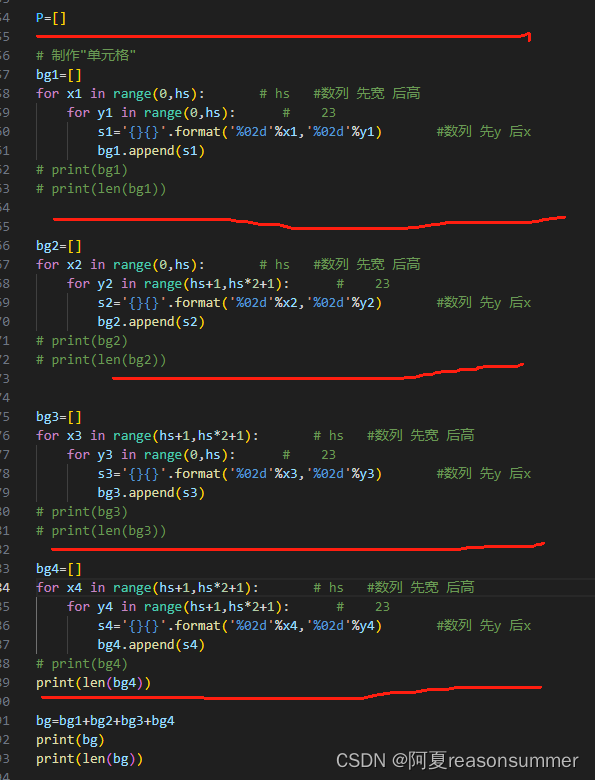
1、以前做单元格填充，都是制作N个分开的单元格
（表格=8）
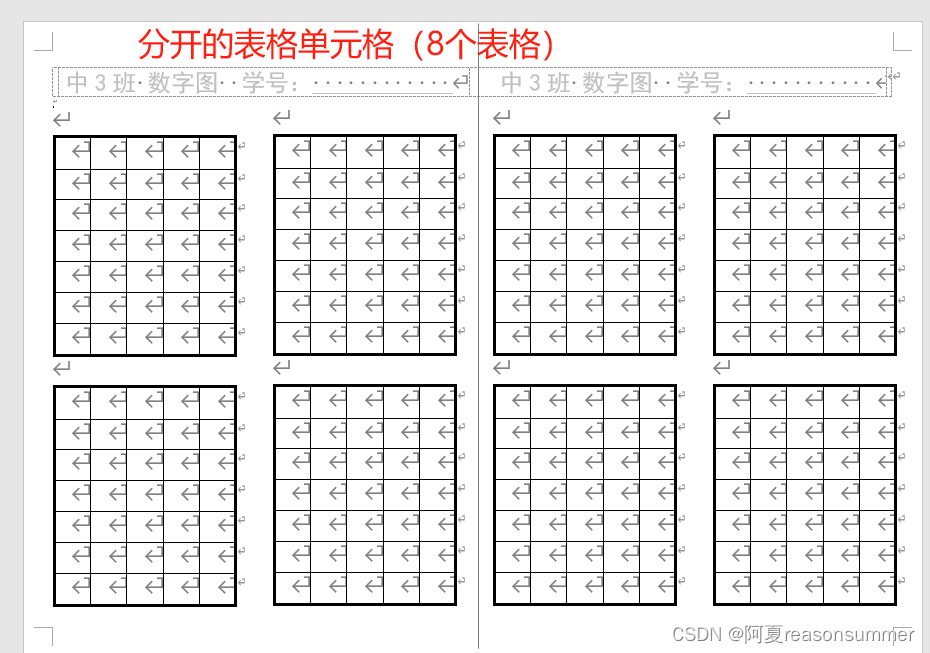
2、这次做五宫格数独的Word模板，我图方便，就只用了一个大表格，第六行第六列隐藏框线，看上去就是分开的，实际还是一个表格（0）
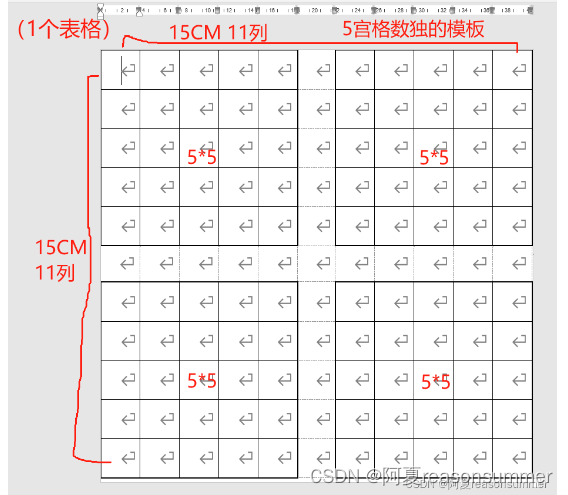
我要提取中间4套5*5的坐标，就需要写四次XY
如果是6*3、9*9，这样的写法就太长了，要写6份，9份
所以，我需要设计一个简略的遍历代码，实现所有填充单元格坐标的提取
设计过程：
工具：AI对话大师
第1问
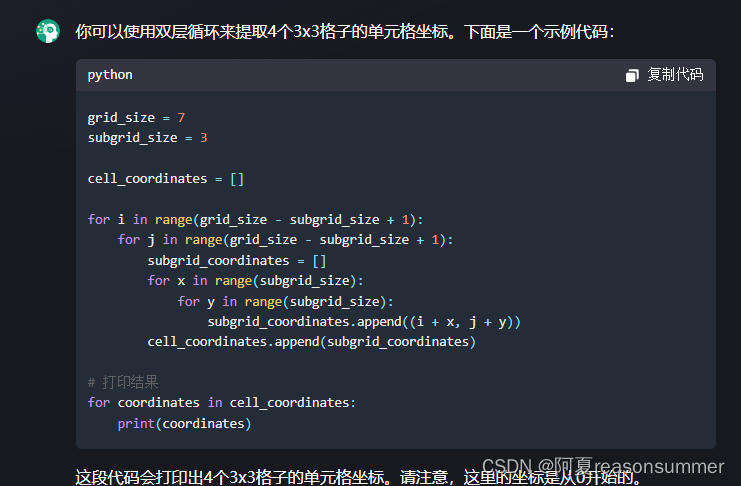
第2问
第3问
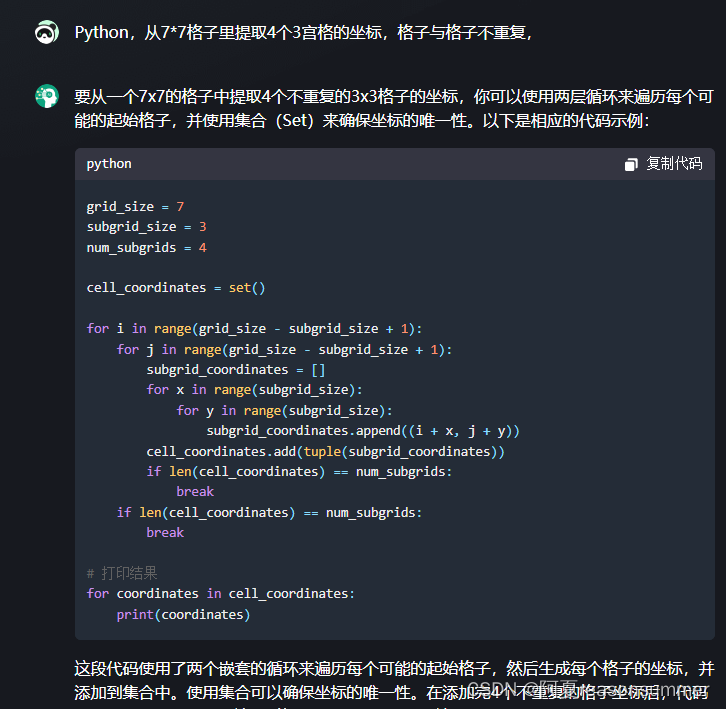第4问
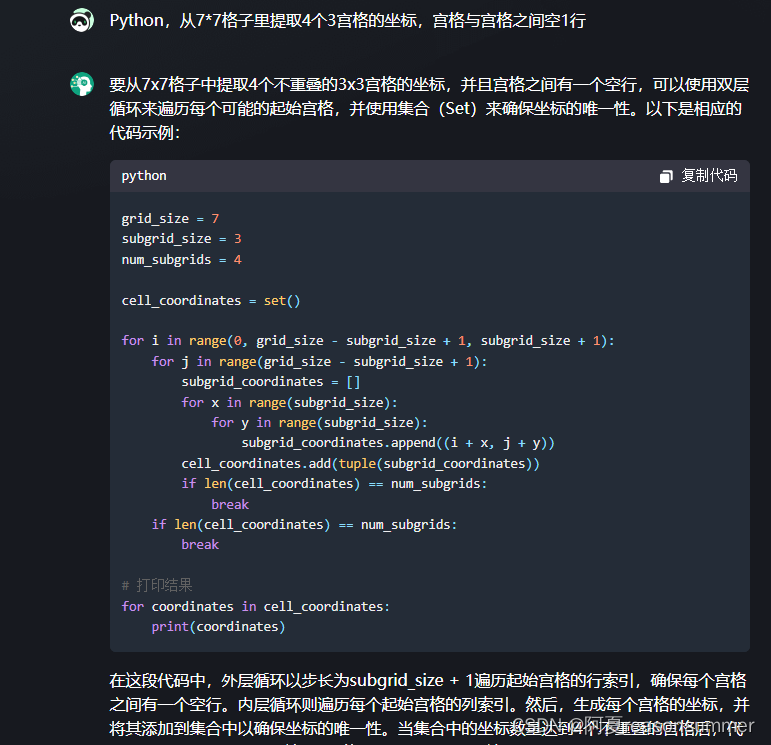第5问——终于出现了我需要的结果
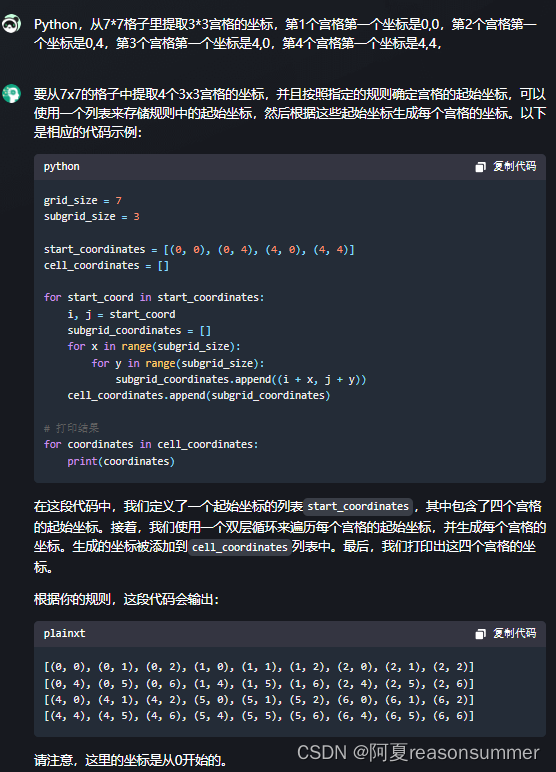
测试1.1：3*3宫格（原始）
# 测试11*11格，2*2一共4套3*3 宫格grid_size = 7
subgrid_size = 3start_coordinates = [(0, 0), (0, 4), (4, 0), (4, 4)]
cell_coordinates = []for start_coord in start_coordinates:i, j = start_coordsubgrid_coordinates = []for x in range(subgrid_size):for y in range(subgrid_size):subgrid_coordinates.append((i + x, j + y))cell_coordinates.append(subgrid_coordinates)bg=[]# 打印结果
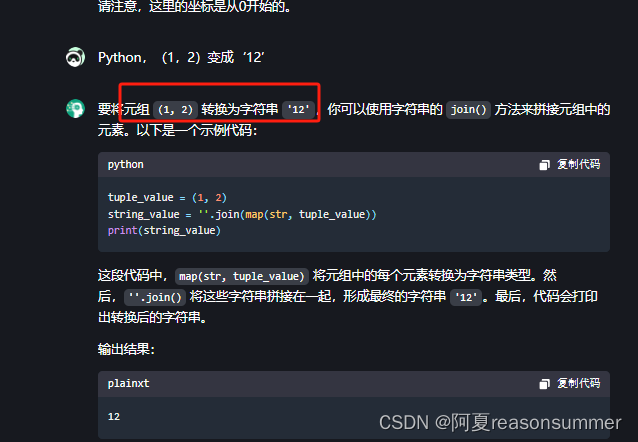
for coordinates in cell_coordinates:# print(coordinates) for c in coordinates:# print(c) # 元组 (1, 2) 样式s = ''.join(map(str, c)) # 元组 (1, 2) 转换为字符串 '12'# print(str(s)) # '12'a1='%02d'%int(s[0]) # '01'a2='%02d'%int(s[1]) # '02'bg.append('{}{}'.format(a1,a2)) # '0102'
print(bg)# 左上 第1套
# ['0000', '0001', '0002',
# '0100', '0101', '0102',
# '0200', '0201', '0202', # 右上 第2套
# '0004', '0005', '0006',
# '0104', '0105', '0106',
# '0204', '0205', '0206', # 左下 第3套
# '0400', '0401', '0402',
# '0500', '0501', '0502',
# '0600', '0601', '0602',# 右下 第4套
# '0404', '0405', '0406',
# '0504', '0505', '0506',
# '0604', '0605', '0606']运行结果
测试2：3*3宫格（改坐标起始参数）
# 测试11*11格，2*2一共4套3*3 宫格
'''
目的：数独09 N宫格X乘Y套单元格计算，如何在一个表格里，找出所有填数字的单元格
以“3宫格”做2*2=4套，“3宫格”做3*2=6套为例
作者：阿夏（参考）
时间：2023年12月31日 13:35
'''
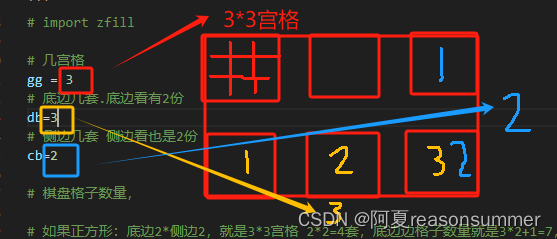
# import zfill# 几宫格
gg = 3
# 底边几套.底边看有2份
db=3
# 侧边几套 侧边看也是2份
cb=2# 棋盘格子数量，# 如果正方形：底边2*侧边2，就是3*3宫格 2*2=4套，底边边格子数量就是3*2+1=7，侧边格子数量就是3*2+1=7，
# 如果长方形：底边3*侧边2，就是3*3宫格，3*2=6套 底边格子数量就是3*3+2=11，侧边格子数量就是3*2+1=7，
# if db==cb:
db_size = gg*db+(db-1)
cb_size= gg*cb+(cb-1)
print('{}宫格排列底{}侧{}共{}套,底边格子数{}'.format(gg,db,cb,db*cb,db_size ))
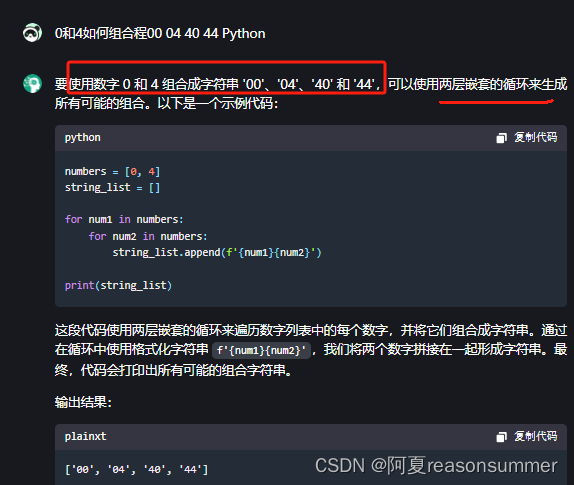
print('{}宫格排列底{}侧{}共{}套,侧边格子数{}'.format(gg,db,cb,db*cb,cb_size ))# 确定每个宫格的左上角坐标 00 04 40 44
bgszm=[]
for a in range(0,cb_size,gg+1): # 0-11每隔4，写一个坐标 侧边yfor b in range(0,db_size,gg+1): # 0-11每隔4，写一个坐标 侧边xbgszm.append('{}{}'.format('%02d'%a,'%02d'%b))
print(bgszm)
# 3宫格排列底3侧2共6套,底边格子数11
# 3宫格排列底3侧2共6套,侧边格子数7
# ['0000', '0004', '0008', '0400', '0404', '0408']# 转为元祖
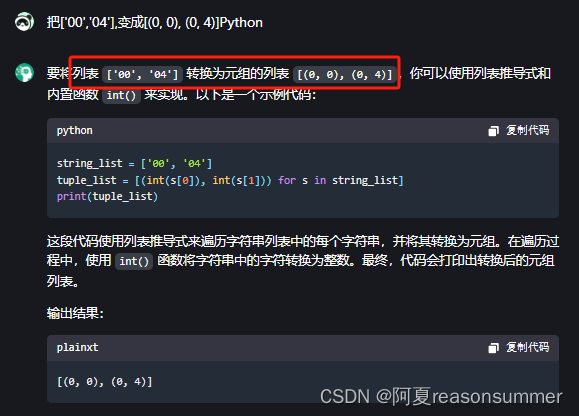
start_coordinates = [(int(s[0:2]), int(s[2:4])) for s in bgszm]
cell_coordinates = []# 推算每个起始格子后面的单元格数字
for start_coord in start_coordinates:i, j = start_coordsubgrid_coordinates = []for x in range(gg):for y in range(gg):subgrid_coordinates.append((i + x, j + y))cell_coordinates.append(subgrid_coordinates)# 打印结果（元祖样式）
bg=[]
for coordinates in cell_coordinates:# print(coordinates) # [(4, 8), (4, 9), (4, 10), (5, 8), (5, 9), (5, 10), (6, 8), (6, 9), (6, 10)]for c in coordinates:print(c) # 元组 (1, 2) 样式s = ''.join(str(num).zfill(2) for num in c) # zfill将元组 (1, 2) 转换为字符串 '0102' 特别是（5,10）这种必须转成2个数字0510print(str(s)) # '12'bg.append(s) # '0102'
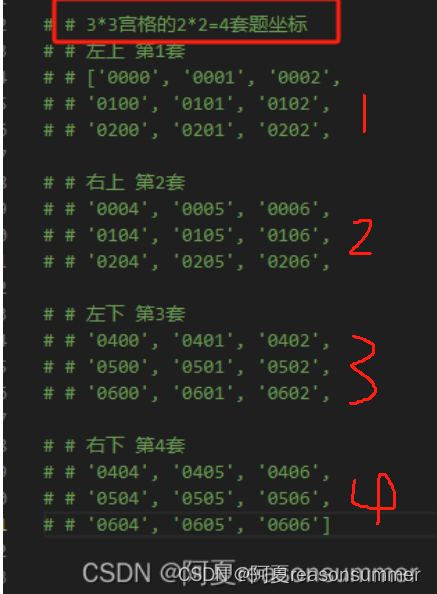
print(bg)# # 3*3宫格的2*2=4套题坐标
# # 左上 第1套
# # ['0000', '0001', '0002',
# # '0100', '0101', '0102',
# # '0200', '0201', '0202', # # 右上 第2套
# # '0004', '0005', '0006',
# # '0104', '0105', '0106',
# # '0204', '0205', '0206', # # 左下 第3套
# # '0400', '0401', '0402',
# # '0500', '0501', '0502',
# # '0600', '0601', '0602',# # 右下 第4套
# # '0404', '0405', '0406',
# # '0504', '0505', '0506',
# # '0604', '0605', '0606']# # 3*3宫格的3*2=6套题坐标# # 3宫格排列底3侧2共6套,底边格子数11
# # 3宫格排列底3侧2共6套,侧边格子数7
# # 6套题的首字坐标['0000', '0004', '0008', '0400', '0404', '0408']
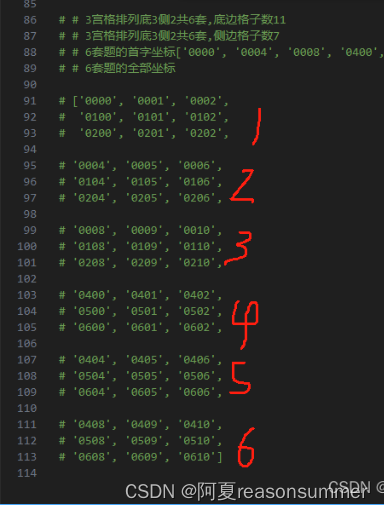
# # 6套题的全部坐标# ['0000', '0001', '0002',
# '0100', '0101', '0102',
# '0200', '0201', '0202', # '0004', '0005', '0006',
# '0104', '0105', '0106',
# '0204', '0205', '0206', # '0008', '0009', '0010',
# '0108', '0109', '0110',
# '0208', '0209', '0210',# '0400', '0401', '0402',
# '0500', '0501', '0502',
# '0600', '0601', '0602', # '0404', '0405', '0406',
# '0504', '0505', '0506',
# '0604', '0605', '0606', # '0408', '0409', '0410',
# '0508', '0509', '0510',
# '0608', '0609', '0610']
3宫格两款：
1、 3宫格 4套（2*2）正方形，
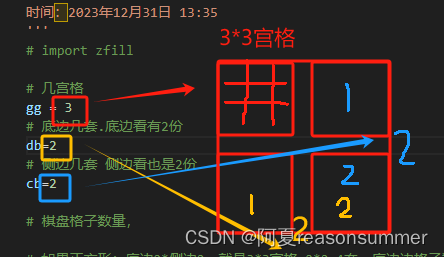
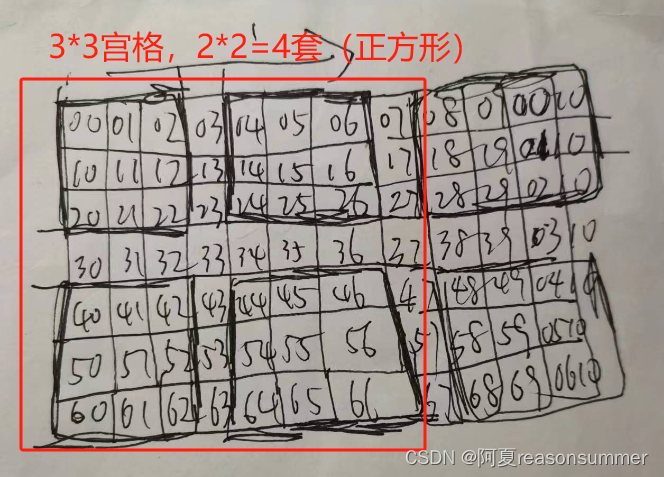
2、3宫格 6套（3*2）长方形
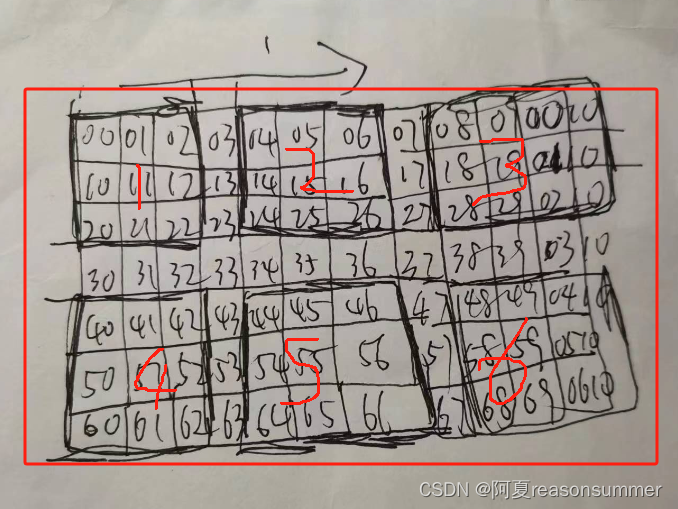
感悟：
代码里面的技术难点 都是用Chat GDP AI对话生成的，提高了数据搜索的效率
这篇关于【教学类-43-11】 20231231 3*3宫格数独提取单元格坐标数字的通用模板（做成2*2=4套、3*2=6套）的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！
