LaTeX中公式：单行间公式，多行间公式，单栏公式，公式跨栏，以及一般论文中的用法

需要提前导入包才可使用以下功能：

\usepackage{amsthm,amsmath,amssymb,lipsum}
\usepackage{mathrsfs}

单行公式比较简单，一般用

\begin{equation}y=x\label{equation1}
\end{equation}

编译结果如下所示：

 \label{}里面是公式标签，可以在别的地方引用这个标签从而引用这个公式，如

\ref{equation1}

的值就是2

但是，一般公式都是多行的，简单的多行公式用

\begin{align}y=x+y+z\label{1}\\y=c+b+n+m\label{2}
\end{align}

编译结果如下所示：

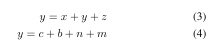
这里的编号仍然是按照（3）,（4）这样的顺序依次编号的；\\为换行符，表示换行；但是公式并没有对齐，格式非常难看，我们使用对齐符号试一下：

\begin{align}y=&x+y+z\label{1}\\y=&c+b+n+m\label{2}
\end{align}

&放在哪里就表示按照哪里对齐。 

如果公式太长需要换行，就需要用到\notag标签避免给不需要的地方编号：

\begin{align}y=&x+y+z\label{1}\\y=&c+b+n+m\label{2}\\y=&a+b+c+g+j+k+l\notag\\&+c+h+p+O	
\end{align}

显示如下：

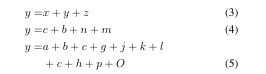
可以看到（5）是一个整体，并没有被分割，因为在上一行使用了\notag

但是如果是括号里的内容需要换行呢？就需要使用虚拟的“括号”，看下面的例子：

\begin{align}y=&x+y+z\label{1}\\y=&c+b+n+m\label{2}\\y=&a+b+c+g+j+k+l\notag\\&+c+h+p+O	\\y=&\left(x+y+x\right.\notag\\&\left.+y+u+i+p\right)
\end{align}

编译结果如（6）：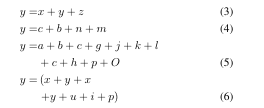

 \right.为虚拟右括号，与\left(这个括号对应；\left.为虚拟左括号，与\right)这个括号对应；也就是说在每一行的公式的括号必须是闭合的，用虚拟的括号代替；如果多个括号以此类推，下面是两个括号的演示：

\begin{align}y=&x+y+z\label{1}\\y=&c+b+n+m\label{2}\\y=&a+b+c+g+j+k+l\notag\\&+c+h+p+O	\\y=&\left(\left( x+y+x\right.\right.\notag\\&\left.\left.+y+u+i+p\right)\right) 
\end{align}

结果如下：

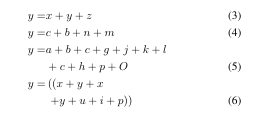
 一般公式中的编号可能为（1a),(1b),(1c)这样的，使用

\begin{subequations}
    \begin{align}
      .....
    \end{align}
\end{subequations}

就可以，如下：

\begin{subequations}\begin{align}y=&x+y+z\label{1}\\y=&c+b+n+m\label{2}\\y=&a+b+c+g+j+k+l\notag\\&+c+h+p+O	\\y=&\left(\left( x+y+x\right.\right.\notag\\&\left.\left.+y+u+i+p\right)\right) \end{align}
\end{subequations}.

编译如下：

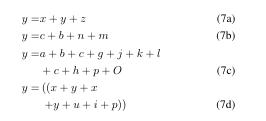
 还有，如果公式太长需要跨栏（双栏）只要使用

\begin{figure*}
    ...
\end{figure*}

嵌套就可以了，其中*就表示双栏，如下：

\begin{figure*}\begin{subequations}\begin{align}y&=a+b\label{1a}\\y&=c+d\label{1b}\end{align}\end{subequations}
\end{figure*}

编译如下：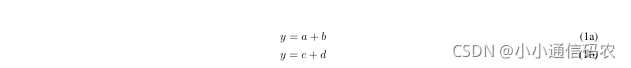

 可以看到，占了双栏。

一般公式在双栏公式下还会有一条很长的线用于分割文本，如下所示加上这一行

{\noindent} \rule[-10pt]{18cm}{0.05em}

就可以

\begin{figure*}\begin{subequations}\begin{align}y&=a+b\label{1a}\\y&=c+d\label{1b}\end{align}\end{subequations}{\noindent} \rule[-10pt]{18cm}{0.05em}
\end{figure*}

结果：

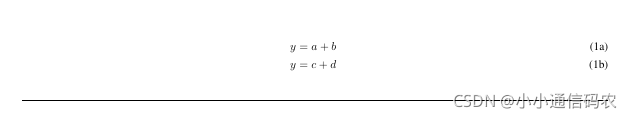
 完结，撒花！