【Matlab】根据伯德图计算pid参数方法原理

在学习鲁棒控制的过程中，有一些步骤需要根据一些性能参数来计算pid参数，因此记录一下根据伯德图的性能来计算pid参数的原理。

系统开环响应的几个关键参数

在使用开环响应初调控制器参数时，主要就是调整几个需要注意的关键参数，相同的，计算控制器参数也是根据关键参数来进行计算的，主要关心的是一下几个参数：

1）相位裕度

2）穿越频率

3）截止频率

相位裕度：相位裕度是系统的开环增益为 0 db 时(穿越频率)，对应相频响应曲线与 -180 度的相位差，用于评估系统的稳定性，相位裕度越大，系统稳定性越好

穿越频率：是指系统幅频响应曲线与 0db 的交点频率，用于评估系统的稳定性

截止频率：是指系统幅频响应曲线与 -3db 相交的频率

其中，穿越频率通常用来衡量系统的相位裕度，截止频率通常用来衡量系统的带宽。当系统满足相位裕度要求时，截止频率越高，系统带宽越大，响应速度越快。

根据伯德图来调整pid参数的中心思路：指定想要的穿越频率，以及在此穿越频率下想要系统达到的相位裕度，之后根据实际系统的频率特性曲线，加入控制器补偿其相位裕度与穿越频率。

单校正环节效果与原理分析

进行整体指标的调整需要用到多个环节，接下来的内容是对单个环节的效果与作用进行分解分析，方便后续合并为整体的计算理解。

超前校正与穿越频率，相位裕度

穿越频率中对应的相频响应曲线，决定相位裕度，超前校正可以用于提升系统的相位裕度。

超前校正的思路是：将相位曲线在某一个频率段向上提升，同时尽量不改变幅值曲线，这样就可以增加系统的相位裕度。

例如以下的一个系统的伯德图，随便给了一个控制器，相位裕度是35.9度，想要抬升其相位裕度：

单个超前或滞后控制器的传递函数表达式为：

w_z < w_p 时，就是超前控制器

w_z > w_p 时，就是滞后控制器

但上述表示方式不容易计算各类参数，需要进行转换。转换有两种方法。

方法一(可能会计算出实际中不合理的值，需要查看计算结果)

超前校正调节器转换为以下的形式：

当 α > 1 时，就是超前校正，小于 1 时，就是滞后校正。

写成这种形式，各种参数比较好算：

1）其上下截止频率为 w1 = 1 / (α*Ta) ，w2 = 1 / Ta

2）最大相位处的频率为：

3）最大相位为

使用一个例子来验证一下，假设穿越频率是 1Hz，需要补偿 30度，让超前校正器的最大相位对应频率对应 1Hz，最大相位为 30度，按照上式计算参数：

%超前校正传递函数
f_lead = 1;  %假设穿越频率为1Hz
compensation_phase = 30;  %假定补偿相位为30度   (α-1)/(α+1) = sin(Φ)   α = (1+sin(Φ)) / (1-sin(Φ))
alpha = (1+sin(compensation_phase / 57.3)) / (1-sin(compensation_phase / 57.3));  %系数，必须大于1，否则会变成滞后校正
Ta = 1 / (f_lead*sqrt(alpha));
a_lead = [alpha*Ta 1];
b_lead = [Ta 1];
lead_K = tf(a_lead, b_lead);  %超前校正传递函数
margin(lead_K);

打印超前校正器的伯德图，与给定一致：

这种方法也是可以的，只是有可能会计算出比较大的 Ta，其实超前校正的分母就对应 PID 控制器中 D 项的滤波器，这种方法会调整滤波器，可能会计算出一个很大的值，在实际中不太合理，需要计算出不合理值后，再重新调整计算。

方法二(与滤波器的值对应，固定其中一个参数)

实际中，对于原始数据的滤波是固定的，因此，可以考虑采用如下的形式：

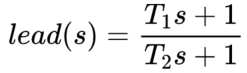
假设实际中使用的是一个 60Hz 的低通滤波，将T2使用 60Hz 固定住，即 T2 = 1 / fc = 0.0167。

这种方法需要放在整体完整的系统中去求解参数，因此先放在这里。

需要注意，理论上超前校正器最多只能补偿 90 度的相位，实际中，会比理论值更小，如果要增加比较大的相位裕度，可以考虑两个超前校正器串联。

类PI控制器调整截止频率

超前校正器用来补偿系统的相位裕度，截止频率可以由 PI 控制器来进行调节：

但上述的 PI 控制器，在实际的计算过程中，发现了许多的弊端，主要有两处：

1）引入了两个变量，k1，k2，导致没有唯一解，

2）两个变量很容易算出负数来，还需要再检查结果，徒增麻烦

因此，需要将上述控制器砍掉一个参数 k2，只留 k1，最终的计算结果就一直是正数，且计算容易：

这是一个类似 PI 的控制器

接下来，使用此控制器来调节系统，进而求解其开环截止频率的步骤可以简述为以下几步(假设控制对象是二阶系统)：

1）将此控制器的传递函数与被控对象传递函数相乘，得到系统的总开环传递函数 KG(s)

2）将 KG(s) 中的 s 用 jw 替代，得到系统的频率响应公式

3）求解 KG(jw) 的幅值为 -3db 时对应的频率 w，即为系统的开环截止频率

系统传递函数为：

加入 PI 控制器的开环传递函数为：

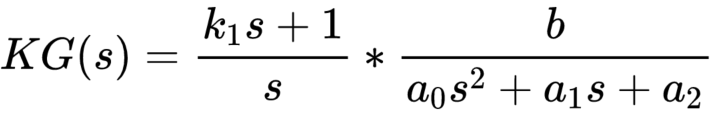
将 s 用 jw 替换，之后写出其幅频响应表达式，之后求解：

此时的幅值对应的 wc 就是截止频率。

求解上述式子需要回顾一些复数计算的公式：

复数的模(幅值)就是其实部，相角是其虚部

再例如，对于以下系统响应：

其幅频响应为：

之后，将 KG 的幅频响应算出：

令其等于 1/sqrt(2) ，也就是列出了截止频率时的方程。

因为是期望截止频率达到想要的值(wc_ref)，也就是说，指定 wc = wc_ref，作为一个已知量，写出 k1 的表达式，求得对应的 k1，就可以使此控制器控制截止频率达到想要的值了：

例如，令 w = 15 hz，求解出来的控制器与系统的开环伯德图与截止频率为：

证明计算是无误的，有一点点的误差关系不大，matlab画图与计算的精度有一些区别，不完全一样关系不大。

增加增益系数调节穿越频率

在控制器的前面，再增加一个系数 k，用于调整幅频响应的增益，就可以调整穿越频率到指定的值上，系数 k 的计算原理也比较简单，求出不加 k 时，整个控制器加系统在期望穿越频率下的幅值，记作 g，然后求倒数赋给 k 即可。

完整控制器与系统联立求解参数

以上是单个环节分析验证，最终是要使用完整的控制器与系统进行计算，系数k，加上控制器，再加上超前校正环节，构成最终的控制器，再加上系统的传递函数：

求解参数时，可以根据自己看重系统的哪些性能来联立方程，例如，给定系统的滤波系数T2，期望的系统截止频率 wn_ref，期望的系统穿越频率 wc_ref，期望的系统相位裕度 PM 。

求解时，先刨除参数 k ，因为系数 k 是用于最后的穿越频率增益补偿的，不过k增加了之后，还是会对整体的截止频率预设计有影响。

可以根据截止频率来确定系统的 k1，滤波系数确定系统的 T2，之后的参数 T1 根据以下的期望相位裕度与穿越频率的方程来计算：

 

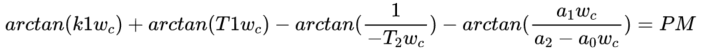
注意：arctan 计算出来是弧度，PM 也要转化为弧度制

在计算完成之后，再根据出去 k 的系统的幅频响应，确定系数 k。

例如，先设置截止频率为 3hz，60Hz 的滤波频率，1.5hz的穿越频率，60度的相位裕度，得出的结果的伯德图为：

 

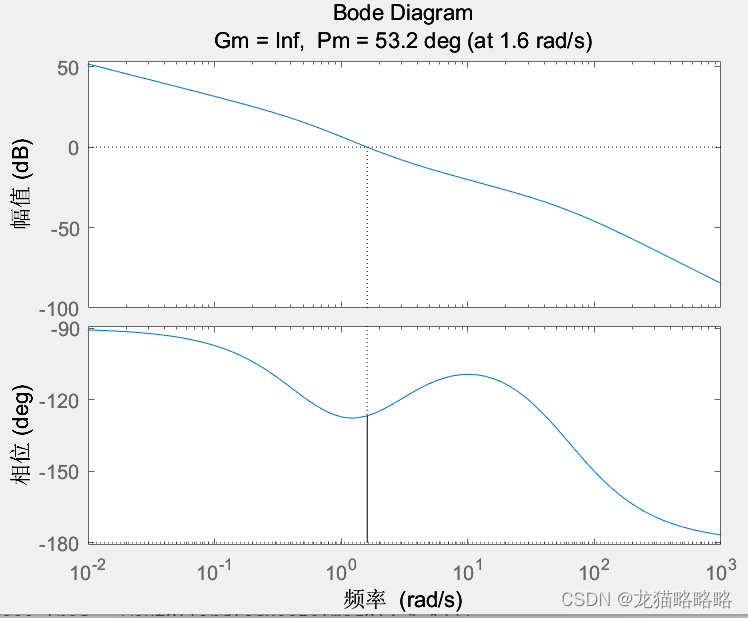
控制器转化为PID参数

完整控制器的传递函数为：

PID控制器的传递函数为：

联立两个方程，可以求解出 PID 的参数的表达式：

Kp = k*k1+k*T1 - k*T2

Ki = k

Kd = k*k1*T1 - Kp*T2

Td = T2

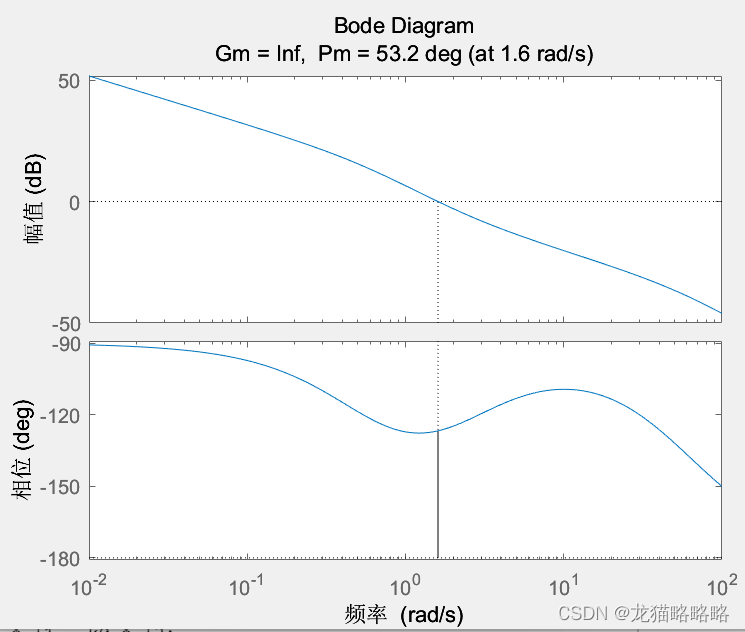
求解出的 PID 控制器的伯德图与上面是一致的：