本文主要是介绍二刷--从上到下打印二叉树 III(层序递归+反转),希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
题目描述
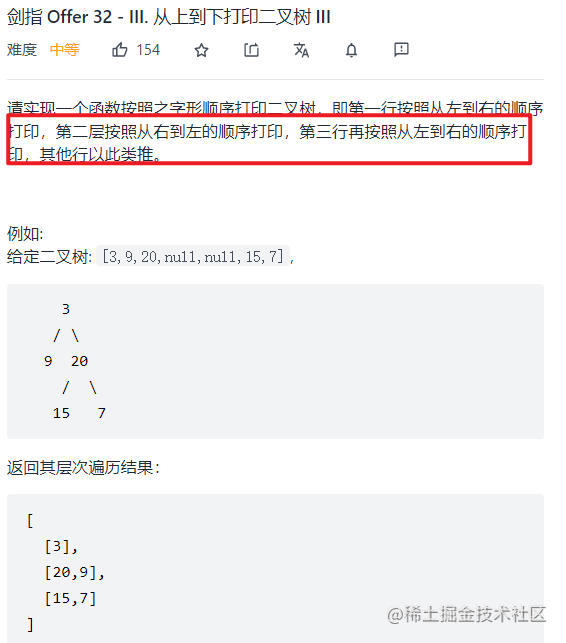
解题思路
实现方式一:递归法进行层序遍历然后根据层次的奇偶进行反转
var levelOrder = function (root) {// 核心思路:二叉树的层序遍历--递归实现if (!root) return [];let result = [];function levelOrder(root,level) {if (!root) return null;result[level] = result这篇关于二刷--从上到下打印二叉树 III(层序递归+反转)的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!





