本文主要是介绍电容篇-电容器件工作原理及参数分析理解,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
编写版本:V1.0
1.电容选型需要注意什么参数?
根据立创商城提供的电容器件筛选条件,可以看出电容选型有以下极管参数需要注意:
- 容值
- 精度
- 耐压值(额定电压)
- 温漂系数(介质材料)
- 封装

另外扩展一下电容的品牌/产地:风华利华(中国),国巨,红宝石(日本),威世(美国)等。
2.电容参数讲解(摘抄自张飞电子电容讲解内容,配合张飞电子视频讲解最佳)
2.1电容的工作原理
我们在分析电路时,经常将电流比喻成水流,分析电路,其实就是分析水流的动态。
电容,我们一般将它理解成为一个水缸,如下图所示,
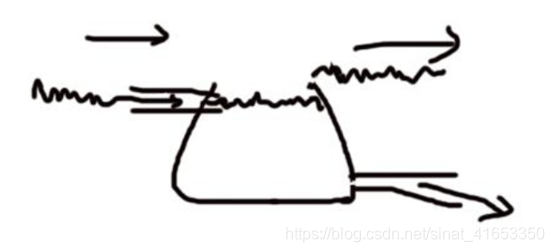
右下角有个管子对外放水,左上角有个管子用来进水,就是外面不稳定的水通过管子流入水缸,注满水缸,就会从右下角的管子排出。
我们发现,当流入的水类似于图中纹波一样(类似AC-DC出来的电流纹波),不稳定,如果它不经过水缸,直接从缸口往外流出,那它还是保持原来不稳定的状态,即水面不平稳。
但是,如果我们把它放在水缸里面,从水缸底部的管子往外排出,这个水就是相当稳定的,最多是造成在缸口处的水平面不稳定。
这个时候我们就说这个水缸起到了滤波的作用。滤除的是输入过来的水的纹波,从缸底部管子输出就是很平稳的,几乎没有什么波动的水。
这个在我们电容的应用中得到很大的启发。
电容对电压的作用,相当于是这个水缸对水的作用,也就是说,这个电容里面储存的是电荷,一个个的正电荷放置在里面,从外面进来的电荷在里面不断的往上堆积,然后再平稳的输出去,电荷数平稳输出且无波动。
因此我们后面电路的负载也就能够得到一个平稳的源源不断的输出。一个平稳,且没有波动的电压,能够让负载更加可靠的工作,也不会对其造成损伤。
所以,我们就需要把负载供电的电压进行滤波,而滤波就是通过电容,用的就是我们刚讲的类似于水缸的原理的方法。
2.2电容的容量
电容的容量是有限的,就像电阻一样,它的单位,我们用法拉(F)来衡量,法拉是电容能储存电荷数大小的单位,常见的单位右微法(uF),纳法(nF),皮法(pF)。
电容单位换算:1法拉=106微法=109纳法=10^12皮法
在实际过程中,我们做不到1法拉这么大的电容,大多数都是微法为量级的。
电路中,电容一般是用来储能用的,就如我们刚讲的类似于水缸的原理,那么电容的大小与水缸有什么关系呢?
如下图所示分析:
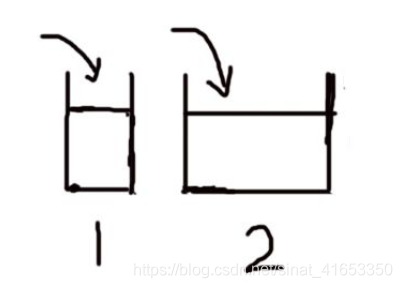
左边的为1号水缸,右边的为2号水缸,这两个水缸,他们的高度是一致的,底面积不一样。
这个时候我们同时都是在这两个水缸里面加水,当我们把水加满的时候或者两水缸的水都加到同一高度的时候,发现2号水缸里面所加的水要远远大于一号水缸,而如果家相同的水,1号水缸里面水位上升的更高,2号水缸里面的水位升的更低。
那我们把这两个水缸类比到电容,我们说电容的单位越大,它的截面积越大,相当于水缸的底面积越大。
如果我们给电容充电且充到一个相同的高度,比如10V,那么我们知道2号电容所需要的电荷数更多,1号电容需要的电荷数更少。
由此,我们引入一个电容公式:C=Q/U,C是电荷容量,Q是电荷数,U是电压,这是个什么意思呢?
就如我们刚把电容比作水缸,那么我们也就认定Q是水缸的体积,U是水缸的高度,C类比于水缸的底面积。
对于水缸来讲,它的高度乘以底面积就等于体积。那么我们也就得到这个公式:Q=C*U,是不是就是我们上面电容的公式。
因此对于一个相同体积的电容来讲,你的底面积C越大,你的水位U就越低,反之电容C越小,电压U就越高。
2.3电容的抗性-容抗与电压电流波形
如下图分析:
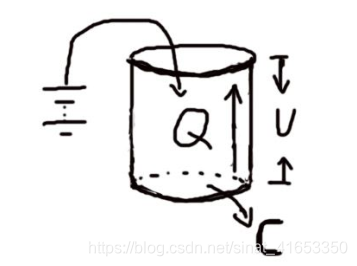
我们把水缸的底面积当作是C,高度就相当于V,在水缸外部有个电源,现在这个电源开始对它充电,也就是把电荷Q啪啪啪啦往水缸里面放,放的过程,电压由低到高开始往上升,并且在充电过程中,电容天生会产生一种抵抗性,阻碍这个充电过程,也即在这个过程中电容有着天生的排斥性,不希望别人往里面加电荷,我们把这种抵抗性称之为容抗。
为了便于理解,我们也可以这样理解,当一个公交车里面挤满了人,来到下一个站台,又有很多人要上公交车,在公交车里面的人自然而然就会产生一种抵抗,不想有更多的人挤上公交车,因此这会导致公交车更挤。
如果从这方面来理解电容,也就是说,当一个外在电源给电容充电的时候,电容它就会呈现出一个天生的抵抗性。
那么我们就先来观察下电容充电时候的电压波形曲线。
如下图分析:

在水缸外面有个电源,比如说,这个电压有30V,当这个30V电源给电容供电,在初始时,电容里面是没有电荷数的,因此电源和电容之间就相差30V的绝对高度。
这时候,如果电荷往电容里面走的话,我们说它的流动速度是非常快的,这就相当于在水箱外部高30米的地方,往水箱里注水,这时候水流的速度是相当快的。
如果这个高度降低了,比如说在15米的地方给水箱注水,我们能够明显看出来它的斜率变小了,也就是说水流速度缓慢了。
因此得出高度越高的,它流入速度越快,可以说,刚开始30V给电容充电的时候,它的斜率是最大的,流动速度也是最快的。我们也可以说在这个时候电荷受到的阻碍力是最小的,也即容抗小,因此我们知道阻碍力越大,容抗越大。
在刚开始,30V给电容充电的这一瞬间,电荷流动速度是最快的,但是,随着充电的过程,水箱的水位是不断的上升,如果水箱高度等效为电压的话,也就是说这电压不断上升,当电容的电压上升到15V的时候,从图中可以看出,可以观察电荷流入电容的方式,这时,我们明显的看出它的斜率变缓了,随着电容中的电压上升,斜坡越来越小,电荷流入电容的速度越来越慢,因此充电的快慢与电源和电容之间的压差有关,压差越大,充电速度越快。
电容呈现出来这一现状,以及上述规律,能够画出电容充电时大概的电压波形。
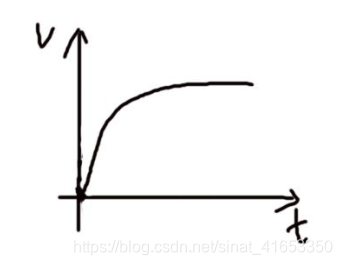
电容充电电压的公式:
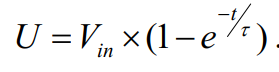
其中Vin为外部电源电压,τ为充电时间常数,τ=RC,这个R时电压源的内阻,C即为电容。
有电压波形自然有电流波形,而电流波形正好与电压波形是相反的,通过以上分析,我们知道,起始时刻,电荷流速最快,因此充电电流是最大的,随着充电时间的推移,电荷流速越来越慢,那么,电流也就越来越小了,因此,充电电流的曲线是递减的。
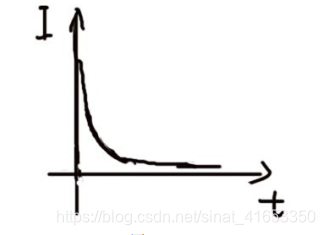
上述内容摘抄之张飞电子电容讲解部分。
这篇关于电容篇-电容器件工作原理及参数分析理解的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!



