本文主要是介绍matlab计算差分方程近似值,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
1.题目
计算3个差分方程的前10个数值近似值,并引入初始误差。并构造表和图的输出。

定义10个数,xn为初始误差,根据差分方程,定义rn/pn/qn的值进行计算,最终返回xn-rn/xn-pn/xn-qn的值,以表格/图片输出。
2.代码
(1)rn与xn-rn计算值
n=0:10;
xn=1./(2.^n)
r0=0.994;r(1)=r0/2;
for n=2:10
r(n)=r(n-1)/2
end
rn=[r0,r];
m=xn-rn;
xn-rn生成图片
r0=0.994;r(1)=r0/2
for n=2:10
r(n)=r(n-1)/2;
end
rn=[r0,r]
n=0:10;
xn=1./(2.^n);
y=xn-rn;
plot(n,y,'.')
xlabel('n');
ylabel('xn-rn');
(2)pn与xn-pn计算值
n=0:10;
xn=1./(2.^n)
p0=1;p(1)=0.497;p(2)=3*p(1)/2-p0/2;
for n=3:10
p(n)=3*p(n-1)/2-p(n-2)/2;
end
pn=[p0,p];
n=xn-pn;
xn-pn生成图片
p0=1;p(1)=0.497;p(2)=3*p(1)/2-p0/2;
for n=3:10
p(n)=3*p(n-1)/2-p(n-2)/2;
end
pn=[p0,p]
n=0:10;
xn=1./(2.^n);
y=xn-pn;
plot(n,y,'.')
xlabel('n');
ylabel('xn-pn');
(3)qn与xn-qn计算值
n=0:10;
xn=1./(2.^n)
q0=1;q(1)=0.497;q(2)=5*q(1)/2-q0;
for n=3:10
q(n)=3*q(n-1)/2-q(n-2)/2
end
qn=[q0,q];
w=xn-qn;
xn-qn生成图片
q0=1;q(1)=0.497;q(2)=5*q(1)/2-q0;
for n=3:10
q(n)=3*q(n-1)/2-q(n-2)/2
end
qn=[q0,q]
n=0:10;
xn=1./(2.^n);
y=xn-qn;
plot(n,y,'.')
xlabel('n');
ylabel('xn-qn');
3.实验结果
(1)差分方程近似值情况汇总如下

(2)差分方程误差{xn-rn}{xn-pn}{xn-qn}生成图片
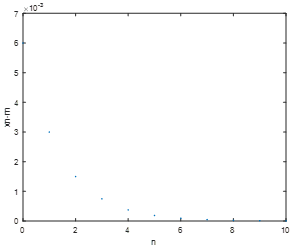
图1 {xn-rn}
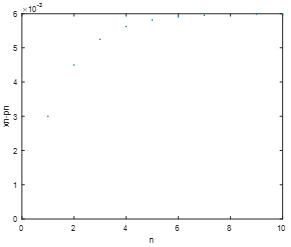
图2 {xn-pn}

图3 {xn-qn}
这篇关于matlab计算差分方程近似值的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!





