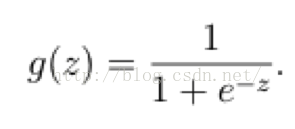本文主要是介绍入门金融风控【贷款违约预测】,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
入门金融风控【贷款违约预测】
赛题以金融风控中的个人信贷为背景,要求选手根据贷款申请人的数据信息预测其是否有违约的可能,以此判断是否通过此项贷款,这是一个典型的分类问题。通过这道赛题来引导大家了解金融风控中的一些业务背景,解决实际问题,帮助竞赛新人进行自我练习、自我提高。
天池比赛
Task01赛题理解
- 赛题概括(见上文)
- 数据概括(了解数据概况)
- 预测指标(学习各种预测指标)
- 分析赛题
数据概括
train.csv
- id 为贷款清单分配的唯一信用证标识
- loanAmnt 贷款金额
- term 贷款期限(year)
- interestRate 贷款利率
- installment 分期付款金额
- grade 贷款等级
- subGrade 贷款等级之子级
- employmentTitle 就业职称
- employmentLength 就业年限(年)
- homeOwnership 借款人在登记时提供的房屋所有权状况
- annualIncome 年收入
- verificationStatus 验证状态
- issueDate 贷款发放的月份
- purpose 借款人在贷款申请时的贷款用途类别
- postCode 借款人在贷款申请中提供的邮政编码的前3位数字
- regionCode 地区编码
- dti 债务收入比
- delinquency_2years 借款人过去2年信用档案中逾期30天以上的违约事件数
- ficoRangeLow 借款人在贷款发放时的fico所属的下限范围
- ficoRangeHigh 借款人在贷款发放时的fico所属的上限范围
- openAcc 借款人信用档案中未结信用额度的数量
- pubRec 贬损公共记录的数量
- pubRecBankruptcies 公开记录清除的数量
- revolBal 信贷周转余额合计
- revolUtil 循环额度利用率,或借款人使用的相对于所有可用循环信贷的信贷金额
- totalAcc 借款人信用档案中当前的信用额度总数
- initialListStatus 贷款的初始列表状态
- applicationType 表明贷款是个人申请还是与两个共同借款人的联合申请
- earliesCreditLine 借款人最早报告的信用额度开立的月份
- title 借款人提供的贷款名称
- policyCode 公开可用的策略_代码=1新产品不公开可用的策略_代码=2
- n系列匿名特征 匿名特征n0-n14,为一些贷款人行为计数特征的处理
预测指标
import pandas as pd
import numpy as np
train=pd.read_csv('train.csv')
testA=pd.read_csv('testA.csv')
print('Train data shape:',train.shape)
print('TestA data shape:',testA.shape)print(train.head())#分类指标评价计算示例##confusion_matrix
from sklearn.metrics import confusion_matrix
y_pred=[0,1,0,1]
y_true=[0,1,1,0]
print('confusion_matrix:\n',confusion_matrix(y_true,y_pred))##accuracy
from sklearn.metrics import accuracy_score
y_pred=[0,1,0,1]
y_true=[0,1,1,0]
print('ACC:',accuracy_score(y_true,y_pred))##Precision,Recall,FL-score
from sklearn import metrics
y_pred=[0,1,0,1]
y_true=[0,1,1,0]
print('Precision:',metrics.precision_score(y_true,y_pred))
print('Recall:',metrics.recall_score(y_true,y_pred))
print('FL-score:',metrics.fl_score(y_true,y_pred))##P-R曲线
import matplotlib.pyplot as plt
from sklearn.metrics import precision_recall_curve
y_pred = [0, 1, 1, 0, 1, 1, 0, 1, 1, 1]
y_true = [0, 1, 1, 0, 1, 0, 1, 1, 0, 1]
precision, recall, thresholds = precision_recall_curve(y_true, y_pred)
plt.plot(precision, recall)## ROC曲线
from sklearn.metrics import roc_curve
y_pred = [0, 1, 1, 0, 1, 1, 0, 1, 1, 1]
y_true = [0, 1, 1, 0, 1, 0, 1, 1, 0, 1]
FPR,TPR,thresholds=roc_curve(y_true, y_pred)
plt.title('ROC')
plt.plot(FPR, TPR,'b')
plt.plot([0,1],[0,1],'r--')
plt.ylabel('TPR')
plt.xlabel('FPR')## AUC
import numpy as np
from sklearn.metrics import roc_auc_score
y_true = np.array([0, 0, 1, 1])
y_scores = np.array([0.1, 0.4, 0.35, 0.8])
print('AUC socre:',roc_auc_score(y_true, y_scores))## KS值 在实际操作时往往使用ROC曲线配合求出KS值
from sklearn.metrics import roc_curve
y_pred = [0, 1, 1, 0, 1, 1, 0, 1, 1, 1]
y_true = [0, 1, 1, 0, 1, 0, 1, 1, 1, 1]
FPR,TPR,thresholds=roc_curve(y_true, y_pred)
KS=abs(FPR-TPR).max()
print('KS值:',KS)
Task02数据分析
- 统计缺失值
- 统计高于50%缺失率的特征
- 可视化缺失特征和缺失率
data_train.head()
| id | loanAmnt | term | interestRate | installment | grade | subGrade | employmentTitle | employmentLength | homeOwnership | … | n5 | n6 | n7 | n8 | n9 | n10 | n11 | n12 | n13 | n14 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0 | 35000.0 | 5 | 19.52 | 917.97 | E | E2 | 320.0 | 2 years | 2 | … | 9.0 | 8.0 | 4.0 | 12.0 | 2.0 | 7.0 | 0.0 | 0.0 | 0.0 | 2.0 |
| 1 | 1 | 18000.0 | 5 | 18.49 | 461.90 | D | D2 | 219843.0 | 5 years | 0 | … | NaN | NaN | NaN | NaN | NaN | 13.0 | NaN | NaN | NaN | NaN |
| 2 | 2 | 12000.0 | 5 | 16.99 | 298.17 | D | D3 | 31698.0 | 8 years | 0 | … | 0.0 | 21.0 | 4.0 | 5.0 | 3.0 | 11.0 | 0.0 | 0.0 | 0.0 | 4.0 |
| 3 | 3 | 11000.0 | 3 | 7.26 | 340.96 | A | A4 | 46854.0 | 10+ years | 1 | … | 16.0 | 4.0 | 7.0 | 21.0 | 6.0 | 9.0 | 0.0 | 0.0 | 0.0 | 1.0 |
| 4 | 4 | 3000.0 | 3 | 12.99 | 101.07 | C | C2 | 54.0 | NaN | 1 | … | 4.0 | 9.0 | 10.0 | 15.0 | 7.0 | 12.0 | 0.0 | 0.0 | 0.0 | 4.0 |
5 rows × 47 columns`
先查看每列数据的缺失情况,将每列缺失率大于50%的特征放进一个列表
have_null_fea_dict = (data_train.isnull().sum()/len(data_train)).to_dict()
fea_null_moreThanHalf = {}
for key,value in have_null_fea_dict.items():if value > 0.5:fea_null_moreThanHalf[key] = value
对特征缺失情况进行可视化
# nan可视化
missing = data_train.isnull().sum()/len(data_train)
missing = missing[missing > 0]
missing.sort_values(inplace=True)
missing.plot.bar()
查看训练集测试集中特征属性只有一值的特征
one_value_fea = [col for col in data_train.columns if data_train[col].nunique() <= 1]
one_value_fea_test = [col for col in data_test_a.columns if data_test_a[col].nunique() <= 1]
查看特征的数值类型有哪些,对象类型有哪些
- 特征一般都是由类别型特征和数值型特征组成,而数值型特征又分为连续型和离散型。
- 类别型特征有时具有非数值关系,有时也具有数值关系。比如‘grade’中的等级A,B,C等,是否只是单纯的分类,还是A优于其他要结合业务判断。
- 数值型特征本是可以直接入模的,但往往风控人员要对其做分箱,转化为WOE编码进而做标准评分卡等操作。从模型效果上来看,特征分箱主要是为了降低变量的复杂性,减少变量噪音对模型的影响,提高自变量和因变量的相关度。从而使模型更加稳定。
numerical_fea = list(data_train.select_dtypes(exclude=['object']).columns)
category_fea = list(filter(lambda x: x not in numerical_fea,list(data_train.columns)))
label='isDefault'
numerical_fea.remove(label)
数值型变量分析——将离散和连续的数值型变量均找出
#过滤数值型类别特征
def get_numerical_serial_fea(data,feas):numerical_serial_fea = []numerical_noserial_fea = []for fea in feas:temp = data[fea].nunique()if temp <= 10:numerical_noserial_fea.append(fea)continuenumerical_serial_fea.append(fea)return numerical_serial_fea,numerical_noserial_fea
numerical_serial_fea,numerical_noserial_fea = get_numerical_serial_fea(data_train,numerical_fea)
数值连续型变量可视化
#每个数字特征得分布可视化
f = pd.melt(data_train, value_vars=numerical_serial_fea)
g = sns.FacetGrid(f, col="variable", col_wrap=2, sharex=False, sharey=False)
g = g.map(sns.distplot, "value")
- 查看某一个数值型变量的分布,查看变量是否符合正态分布,如果不符合正太分布的变量可以log化后再观察下是否符合正态分布。
- 如果想统一处理一批数据变标准化 必须把这些之前已经正态化的数据提出
- 正态化的原因:一些情况下正态非正态可以让模型更快的收敛,一些模型要求数据正态(eg. GMM、KNN),保证数据不要过偏态即可,过于偏态可能会影响模型预测结果。
非数值型变量分析,使用value_counts()
对单一变量的可视化分析
python的数据透视图
#透视图 索引可以有多个,“columns(列)”是可选的,聚合函数aggfunc最后是被应用到了变量“values”中你所列举的项目上。
pivot = pd.pivot_table(data_train, index=['grade'], columns=['issueDateDT'], values=['loanAmnt'], aggfunc=np.sum)
pivot
| loanAmnt | |||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| issueDateDT | 0 | 30 | 61 | 92 | 122 | 153 | 183 | 214 | 245 | 274 | ... | 3926 | 3957 | 3987 | 4018 | 4048 | 4079 | 4110 | 4140 | 4171 | 4201 |
| grade | |||||||||||||||||||||
| A | NaN | 53650.0 | 42000.0 | 19500.0 | 34425.0 | 63950.0 | 43500.0 | 168825.0 | 85600.0 | 101825.0 | ... | 13093850.0 | 11757325.0 | 11945975.0 | 9144000.0 | 7977650.0 | 6888900.0 | 5109800.0 | 3919275.0 | 2694025.0 | 2245625.0 |
| B | NaN | 13000.0 | 24000.0 | 32125.0 | 7025.0 | 95750.0 | 164300.0 | 303175.0 | 434425.0 | 538450.0 | ... | 16863100.0 | 17275175.0 | 16217500.0 | 11431350.0 | 8967750.0 | 7572725.0 | 4884600.0 | 4329400.0 | 3922575.0 | 3257100.0 |
| C | NaN | 68750.0 | 8175.0 | 10000.0 | 61800.0 | 52550.0 | 175375.0 | 151100.0 | 243725.0 | 393150.0 | ... | 17502375.0 | 17471500.0 | 16111225.0 | 11973675.0 | 10184450.0 | 7765000.0 | 5354450.0 | 4552600.0 | 2870050.0 | 2246250.0 |
| D | NaN | NaN | 5500.0 | 2850.0 | 28625.0 | NaN | 167975.0 | 171325.0 | 192900.0 | 269325.0 | ... | 11403075.0 | 10964150.0 | 10747675.0 | 7082050.0 | 7189625.0 | 5195700.0 | 3455175.0 | 3038500.0 | 2452375.0 | 1771750.0 |
| E | 7500.0 | NaN | 10000.0 | NaN | 17975.0 | 1500.0 | 94375.0 | 116450.0 | 42000.0 | 139775.0 | ... | 3983050.0 | 3410125.0 | 3107150.0 | 2341825.0 | 2225675.0 | 1643675.0 | 1091025.0 | 1131625.0 | 883950.0 | 802425.0 |
| F | NaN | NaN | 31250.0 | 2125.0 | NaN | NaN | NaN | 49000.0 | 27000.0 | 43000.0 | ... | 1074175.0 | 868925.0 | 761675.0 | 685325.0 | 665750.0 | 685200.0 | 316700.0 | 315075.0 | 72300.0 | NaN |
| G | NaN | NaN | NaN | NaN | NaN | NaN | NaN | 24625.0 | NaN | NaN | ... | 56100.0 | 243275.0 | 224825.0 | 64050.0 | 198575.0 | 245825.0 | 53125.0 | 23750.0 | 25100.0 | 1000.0 |
7 rows × 139 columns
Task03特征工程
特征预处理
缺失值填充
- 把所有缺失值替换为指定的值0 data_train=data_train.fillna(0)
- 纵向用缺失值上面的值替换缺失值 data_train=data_train.fillna(axis=0,method=‘ffill’)
- 纵向用缺失值下面的值替换缺失值,且设置最多只填充两个连续的缺失值 data_train=data_train.fillna(axis=0,method=‘bfill’,limit=2)
#按照平均数填充数值型特征
data_train[numerical_fea] = data_train[numerical_fea].fillna(data_train[numerical_fea].median())
data_test_a[numerical_fea] = data_test_a[numerical_fea].fillna(data_train[numerical_fea].median())
#按照众数填充类别型特征
data_train[category_fea] = data_train[category_fea].fillna(data_train[category_fea].mode())
data_test_a[category_fea] = data_test_a[category_fea].fillna(data_train[category_fea].mode())
填充后查看数据信息:data_train.isnull().sum(),发现类别特征中issueDate标签需转换为datetime格式
#转化成时间格式
for data in [data_train, data_test_a]:data['issueDate'] = pd.to_datetime(data['issueDate'],format='%Y-%m-%d')startdate = datetime.datetime.strptime('2007-06-01', '%Y-%m-%d')#构造时间特征data['issueDateDT'] = data['issueDate'].apply(lambda x: x-startdate).dt.days
查看对象类型标签employmentLength
1 year 52489
10+ years 262753
2 years 72358
3 years 64152
4 years 47985
5 years 50102
6 years 37254
7 years 35407
8 years 36192
9 years 30272
< 1 year 64237
NaN 46799
Name: employmentLength, dtype: int64
将该对象类型特征转换为数值型
def employmentLength_to_int(s):if pd.isnull(s):return selse:return np.int8(s.split()[0])
for data in [data_train, data_test_a]:data['employmentLength'].replace(to_replace='10+ years', value='10 years', inplace=True)data['employmentLength'].replace('< 1 year', '0 years', inplace=True)data['employmentLength'] = data['employmentLength'].apply(employmentLength_to_int)
查看处理后的数据信息
data['employmentLength'].value_counts(dropna=False).sort_index()
0.0 15989
1.0 13182
2.0 18207
3.0 16011
4.0 11833
5.0 12543
6.0 9328
7.0 8823
8.0 8976
9.0 7594
10.0 65772
NaN 11742
Name: employmentLength, dtype: int64
同理对earliesCreditLine进行处理
异常值处理
Task04建模与调参
金融风控领域常用的机器学习模型主要有:逻辑回归模型、树模型、集成模型。我们将初步理解模型,学习模型的应用,了解模型的优缺点。对于集成模型我们主要学习基于bagging思想(随机森林模型)和基于boosting思想(XGBoost模型、LightGBM模型、CatBoost模型)的两类模型,最后我们将对三大类模型进行模型对比与性能评估,了解学习模型调参方法,具体有:贪心调参方法、网格调参方法、贝叶斯调参方法。
逻辑回归模型
它的核心思想是,如果线性回归的结果输出是一个连续值,而值的范围是无法限定的,那我们有没有办法把这个结果值映射为可以帮助我们判断的结果呢。而如果输出结果是 (0,1) 的一个概率值,这个问题就很清楚了。我们在数学上找了一圈,还真就找着这样一个简单的函数了,就是很神奇的sigmoid函数(如下):
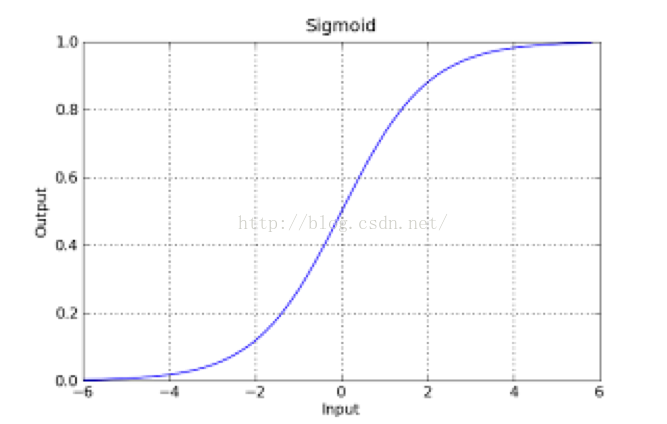
如果把sigmoid函数图像画出来,是如下的样子:
从函数图上可以看出,函数y=g(z)在z=0的时候取值为1/2,而随着z逐渐变小,函数值趋于0,z逐渐变大的同时函数值逐渐趋于1,而这正是一个概率的范围。
所以我们定义线性回归的预测函数为Y=WTX,那么逻辑回归的输出Y= g(WTX),其中y=g(z)函数正是上述sigmoid函数(或者简单叫做S形函数)。
优缺点
-
优点
- 训练速度较快,分类的时候,计算量仅仅只和特征的数目相关;
- 简单易理解,模型的可解释性非常好,从特征的权重可以看到不同的特征对最后结果的影响;
- 适合二分类问题,不需要缩放输入特征;
- 内存资源占用小,只需要存储各个维度的特征值;
-
缺点
-
逻辑回归需要预先处理缺失值和异常值【可参考task3特征工程】;
-
不能用Logistic回归去解决非线性问题,因为Logistic的决策面是线性的;
-
对多重共线性数据较为敏感,且很难处理数据不平衡的问题;
-
准确率并不是很高,因为形式非常简单,很难去拟合数据的真实分布;
-
代码实现
Task05模型融合
模型融合部分的理论知识我还没有完全理解清楚~,所以这里暂时先对相关知识做些学习性记录。
- 回归任务中的加权融合与分类任务中的Voting
- Boosting和Bagging的原理与对比
- Stacking/Blending构建多层模型
5.1.1回归任务的加权融合
加权融合中的【加权】体现了本方法的核心思想,就是根据各个模型的最终预测【结果】表现力分配不同的权重以改变其对最终结果影响的大小。对于正确率低的模型基于更低的权重,而正确率更高的模型给予更高的权重。
#生成一些简单的样本数据, test_prei代表第i个模型的预测值,即模型结果
test_pre1 = [1.2, 3.2, 2.1, 6.2]
test_pre2 = [0.9, 3.1, 2.0, 5.9]
test_pre3 = [1.1, 2.9, 2.2, 6.0]# y_test_true 代表模型的真实值
y_test_true = [1, 3, 2, 6]# 可以先看一下各个模型的预测结果
print('Pred1 MAE:',mean_absolute_error(y_test_true, test_pre1))
print('Pred2 MAE:',mean_absolute_error(y_test_true, test_pre2))
print('Pred3 MAE:',mean_absolute_error(y_test_true, test_pre3))## 结果:
Pred1 MAE: 0.1750000000000001
Pred2 MAE: 0.07499999999999993
Pred3 MAE: 0.10000000000000009下面我们进行对三个模型的加权融合,看看最终的结果
# 下面我们进行加权融合
def Weighted_method(test_pre1, test_pre2, test_pre3, w=[1/3, 1/3, 1/3]):Weighted_result = w[0] * pd.Series(test_pre1) + w[1] * pd.Series(test_pre2) + w[2] * pd.Series(test_pre3)return Weighted_result# 根据上面的MAE,我们计算每个模型的权重, 计算方式就是: wi = mae(i) / sum(mae)
w = [0.3, 0.4, 0.3]
Weighted_pre = Weighted_method(test_pre1,test_pre2,test_pre3,w)
print('Weighted_pre MAE:',mean_absolute_error(y_test_true, Weighted_pre)) # 会发现这个效果会提高一些## 结果:
Weighted_pre MAE: 0.05750000000000027结果显示融合后的Weighted_pre模型效果更好,除了加权平均方法,还可以采用平均值和中位数,但效果没有加权融合好。
5.1.2分类任务中的Voting
联系生活实际,投票一词意思是从众多候选者中选择票数多的那个。在模型融合中体现为:选择所有机器学习算法当中输出最多的那个类。机器学习的算法有很多,对于每一种机器学习算法,考虑问题的方式都略微有所不同,所以对于同一个问题,不同的算法可能会给出不同的结果,那么在这种情况下,我们选择哪个算法的结果作为最终结果呢?那么此时,我们完全可以把多种算法集中起来,让不同算法对同一种问题都进行预测,最终少数服从多数,这就是集成学习的思路。
在不改变模型的情况下,直接对各个不同的模型预测的结果,进行投票或者平均,这是一种简单却行之有效的融合方式。比如对于分类问题,假设有三个相互独立的模型,每个正确率都是70%,采用少数服从多数的方式进行投票。那么最终的正确率将是:

即结果经过简单的投票,使得正确率提升了8%。这是一个简单的概率学问题——如果进行投票的模型越多,那么显然其结果将会更好。但是其前提条件是模型之间相互独立,结果之间没有相关性。越相近的模型进行融合,融合效果也会越差。 有人问这个是怎么算的? 其实就是在少数服从多数算正确率 (三个0.7相乘,就是我三个模型都预测对的概率, 后面的那部分就是我有两个模型预测对了,一个预测错了,那我还是挺预测对了的,这个概率就是后面那个,*3是因为这种情况有三种), 具体详情可以参考这篇博客:模型融合方法学习总结, 这里就不对原理部分解释太多了,少数服从多数的投票方式也比较好理解,关键我们怎么实现这种方式呢?
这篇关于入门金融风控【贷款违约预测】的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!