本文主要是介绍哈夫曼树生成、编码、译码,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
1.任务要求
将英文字符的统计概率作为权值。编程得出哈夫曼的码表;输入一段英文字符,利用码表对其编码、译码。
开发环境: VS2015(C++)
2.数据处理
数据归一化,使各英文字符概率之和为1。由于文献中各字符概率之和大于1,对数据进行归一化。将当前各字符概率值除以当前的概率之和,得出的结果保留小数点后5位,作为新的概率值(相当于权值,这步可以省略,不影响最后结果)。
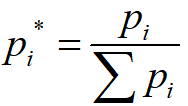
归一化后个字符概率如下图所示。经过检验,归一化之前的概率之和:1.2069;归一化后的概率之和:1.0000。

3.建立哈夫曼树
哈夫曼树(Huffman)即最优二叉树,它是在n个权重作为叶子结点的数值构成的二叉树中,选取并实现带权路径长度(WPL)最短的二叉树。要构造一棵最优二叉查找树就应在离根结点比较近的地方放置查找概率高的结点。
定义两个结构体,分别用于存储字符信息和哈夫曼树结点信息。
typedef struct Alphabet
{ //字符结构体char data;//字符 double probability;//概率值char *code;//编码
} English;
节点信息结构体,用于生成哈夫曼树和实现译码操作。
typedef struct Node
{ //节点结构体double weight;//权值int id;//编号bool visit;//是否加入树中struct Node *right;//右子节点struct Node *left;//左子节点const English *point;//字符信息
} *HuffmanTree;
一个哈夫曼树如果存在n个待编码的叶子节点,一定存在n-1个非叶子节点。节点总数为2n-1个[2]。
首先初始化所有节点,分配存储空间。定义0-26号节点为叶子节点,point指针按照概率值的大小依次指向字符结构体元素。27-52号节点非叶子节点,point指针指向NULL,左右子节点也为NULL。
然后,进行n-1次循环建立哈夫曼树。首先在结构体数组中找出当前权值最小的两个节点(当新生成的节点权值和叶子节点相同时,选择之前的叶子节点),返回它们的位置到minP数组中。再将这两节点合成新的节点,用两者的概率之和合成新节点的权值。
生成树的关键代码如下所示。
for (i = N; i < total; ++i){FindLittleNode(HT, i - N);//找出当前概率值最小的两个节点(*HT)[i].left = (struct Node *)(*HT + minP[0]);(*HT)[i].right = (struct Node *)(*HT + minP[1]);(*HT)[i].weight = (*HT + minP[0])->weight + (*HT + minP[1])->weight;(*HT)[i].point = NULL;printf("%2d \t %.4f \t %2d \t %.4f \t %4d \t\t %.4f\n", minP[0], (*HT + minP[0])->weight, minP[1], (*HT + minP[1])->weight, i,(*HT)[i].weight);cout << endl;
}
寻找最小概率值节点,核心代码如下所示。一次遍历,选出将当前未被加入树中的两个最小节点。得出它们的位置信息。
for (int i = n + 1; i < n + N; i++){if ((*tree)[i].visit){continue;}if ((*tree + i)->weight < min1){min2 = min1;minP[1] = minP[0];//将最小数值及位置赋值到min1和minP[0]中min1 = (*tree + i)->weight;minP[0] = i;}else if ((*tree + i)->weight < min2){//次小值节点信息
min2 = (*tree + i)->weight;minP[1] = i;}
}
4.生成哈夫曼码表
在哈夫曼树创建完成后,利用递归算法进行前序遍历。在遍历过程中,将得出的编码序列存储在字符结构体中。
如果左节点存在,编码序列末尾添加0;如果右节点存在,编码序列末尾添加1;如果节点为叶子节点,将当前遍历得出的编码序列复制到字符结构体的编码信息中。关键代码如下所示。
void enCode(HuffmanTree HT, string code, English *en){if (HT){if (HT->point != NULL){(en + HT->id)->code = (char *)malloc(sizeof(char) * code.length());strcpy((en + HT->id)->code, code.c_str());}enCode(HT->left, code + "0", en);enCode(HT->right, code + "1", en);}
}
5.编码
在生成码表的时候已将字符编码信息保存至字符结构体中。根据输入的英文序列遍历一次即可得出,程序如下所示。
- 首先将字符结构体按照字符ASCII值排序(升序)。
- 读取需要编码是英文字符序列,逐一判断。如果是空格符,取结构体数组的第一个编码;否则,取字符结构体数组第n位的编码。
- 将读取的编码逐一加入新的string对象中,可得到编码的01序列。
string AfterEncode(English *en, string str){string res;string::iterator it = str.begin();while (it != str.end()){if (*it == ' '){res += en->code;}else{res += (en + (*it) - 64)->code;}++it;}return res;
}
将生成的01序列,按照bit来存储传输可以显著降低原英文序列的大小。
6.译码
经过编码后的英文字符序列变为了‘0’‘1’序列,将得出的序列根据哈夫曼树遍历一次即可解出原始英文序列。程序流程如下图所示。
首先判断当前编码序列是0还是1。若为0,访问左节点;若为1,访问右节点。以此进行遍历,直到访问到叶子节点。再回到根节点进行下一编码序列的解码。

string AfterDecCode(HuffmanTree HT, string encstr){string decstr;HuffmanTree p;p = HT + 52;//指向根节点string::iterator it = encstr.begin();while (it != encstr.end()){if (*it == '0')p = p->left;if (*it == '1')p = p->right;if (p->point != NULL){decstr += p->point->data;//回到根节点p = HT + 2 * N - 2;}++it;}
return decstr;}
7.结果展示
7.1建树过程

7.2 哈夫曼树结构

7.3 码表

7.4 编译码过程
自己定义输入一段英文字符序列(不含空格以外的其它符号),程序会自动将输入的序列转换为大写字符。
首先,程序会自动打印出编码后的01序列;然后根据该01序列译码得出原始的英文序列

8. 程序示例
#include <iostream>
#include <string>
#include <string.h>
#include <algorithm>
#include <malloc.h>
#include <bitset>
using namespace std;#define N 27
#define _MAX INFINITYint main()
{English en[27] = { { ' ', 0.2 },{ 'A', 0.063, },{ 'B', 0.0105 },{ 'C', 0.023 },{ 'D', 0.035 },{ 'E', 0.105 },{ 'F', 0.225 },{ 'G', 0.011 },{ 'H', 0.047 },{ 'I', 0.055 },{ 'J', 0.001 },{ 'K', 0.003, },{ 'L', 0.029 },{ 'M', 0.021 },{ 'N', 0.059 },{ 'O', 0.0654 },{ 'P', 0.0175 },{ 'Q', 0.001 },{ 'R', 0.054 },{ 'S', 0.052 },{ 'T', 0.072 },{ 'U', 0.0225 },{ 'V', 0.008 },{ 'W', 0.012 },{ 'X', 0.002 },{ 'Y', 0.012 },{ 'Z', 0.001 }};//数据归一化,使概率和为1double sum = 0;for (int i = 0; i < N; ++i) {sum += en[i].probability;}cout << "概率之和: " << sum << endl;for (int i = 0; i < N; ++i) {en[i].probability = en[i].probability / sum;en[i].probability = (int)(en[i].probability * 100000 + 0.5)*1.0/ 100000.0;}sum = 0;for (int i = 0; i < N; ++i) {sum += en[i].probability;}printf("归一化后,概率之和:%.4f\n", sum);//英文字符排序sort(en, en + N, compare1);//输出英文字符信息//for (char i = 0; i < 27; ++i) {// cout << en[i].data << " " << en[i].probability << endl;//}HuffmanTree Tree;CreateHuffmanTree(&Tree, en);cout << "生成哈夫曼树结构如下:" << endl;PrintHuffmanTree(Tree + 52);cout <<"哈夫曼码表如下"<< endl;enCode(Tree + 52, "", en);cout << "输入一段英文字符" << endl;string myWords, encString, decString;getline(std::cin, myWords, '\n');//读取到换行符才停止transform(myWords.begin(), myWords.end(), myWords.begin(), ::toupper);cout << "输入字符如下(大写):" << endl;cout << myWords << endl;//按照字符ASCII值排序sort(en, en + N, compare2);//输出英文字符码表信息cout << "字符\t权重\t编码" << endl;for (char i = 0; i < N; ++i){cout << en[i].data << "\t" << en[i].probability << "\t" << en[i].code << endl;}cout << "编码之后:" << endl;encString = AfterEncode(en, myWords);cout << encString << endl;sort(en, en + N, compare1);cout << "解码之后:" << endl;decString = AfterDecCode(Tree, encString);cout << decString << endl;system("pause");return 0;
}
这篇关于哈夫曼树生成、编码、译码的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!




