阻尼函数及实现

本文主要是介绍阻尼函数及实现，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

对数衰减方法阻尼振荡

阻尼（damping）是指摇荡系统或振动系统受到阻滞使能量随时间而耗散的物理现象

阻尼振动是指，由于振动系统受到摩擦和介质阻力或其他能耗而使振幅随时间逐渐衰减的振动，又称减幅振动、衰减振动。

不论是弹簧振子还是单摆由于外界的摩擦和介质阻力总是存在，在振动过程中要不断克服外界阻力做功，消耗能量，振幅就会逐渐减小，经过一段时间，振动就会完全停下来。这种振幅随时间减小的振动称为阻尼振动．

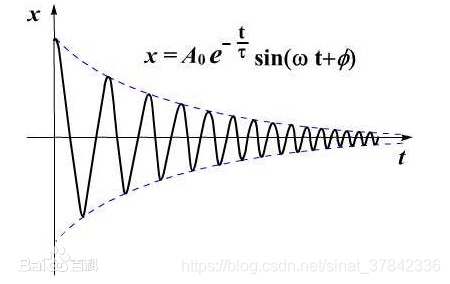
1. 阻尼有助于减小机槭结构的共振振幅，从而避免结构因动应力达到极限造成结构破坏 。
2. 阻尼有助于机械系统受到瞬时冲击后，很快恢复到稳定状态 。
3. 阻尼有助于减少因机械振动产生的声辐射，降低机械性噪声。
4. 可以提高各类机床、仪器等的加工精度、测量精度和工作精度。
5. 阻尼有助于降低结构传递振动的能力。

python实现

import os
import os.path
import sysimport matplotlib.pyplot as plt
import numpy as np# 支持中文
plt.rcParams['font.sans-serif'] = ['SimHei']    # 用来正常显示中文标签
plt.rcParams['axes.unicode_minus'] = False      # 用来正常显示负号def pic_1():def f(t):'''阻尼正弦波计算公式'''s1 = np.sin(2 * np.pi * t + np.pi/3)    # 余弦e1 = np.exp(-t)               # 自然数e的幂return s1 * e1def f2(t):return 0.5 * np.cos(t ** 2) + 0.8plt.xticks([np.pi / 3, np.pi * 2 / 3, np.pi, np.pi * 4 / 3, np.pi * 5 / 3],[r'$\pi/3$', r'$2\pi/3$', r'$\pi$', r'$4\pi/3$', r'$5\pi/3$'])t1 = np.arange(0, 5.0 * np.pi / 3, 0.1)      # 定义x轴(可以将步长改小，图像就很明显)# 曲线1 注意label的写法带有罗马字符l1 = plt.plot(t1, f(t1), color='red', linewidth=1, linestyle="-", label=r"exp$_\delta$ecay")result = f(t1)print(result)# 标题 横纵轴描述plt.title(u"阻尼衰减曲线")plt.xlabel("时间(s)")plt.ylabel("幅度(mV)")# 图例位置plt.legend(loc='upper right')plt.show()if __name__ == "__main__":pic_1()

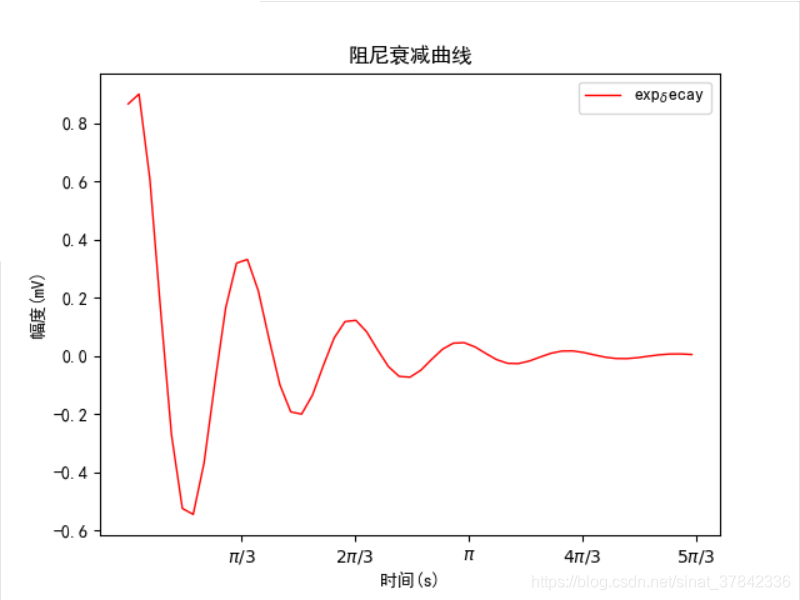
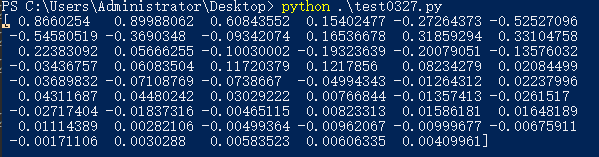
C++实现

#include <QDebug>
#include "math.h"#define PI 3.14159265
//幅值A0//角速度W//角位移B//时间t
double calue(double A0,double W,double B,double t)
{double s1 = sin(W*t + B);double e1 = A0 * exp(-t);return s1*e1;
}int main(int argc, char *argv[])
{for(double t = 0; t<5*PI/3; t+=0.1){qDebug() << calue(1,2*PI,PI/3,t);}
}

这篇关于阻尼函数及实现的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---